-Giải câu 1b .
Viết phương trình tiếp tuyến tại điểm trên ( C ) có hoành độ là - 1 .
Tìm tung độ của điểm M @ ( C ) : x = -1
-Chọn Calculus , Functions and Their Graphs ->
 | Evaluating Function |
-Nhập biểu thức : x^3-3*x^2-9*x+1 vào f(x) = , và x = -1 vào ô Enter Problem .
-Ở Select Topics chọn Evaluate the Function .
-Nhấn Show để xem định dạng toán của hàm số ( Math Format ) , kiểm tra xem có đúng với đề bài không .
-Nhấn Answer để xem tung độ của điểm M .
-Như vậy điểm M(-1 ; 6) @ (C) .
Tương tự tìm giá trị của đạo hàm tại x = -1 .
-Phương trình tiếp tuyến với ( C ) tại M(-1 ; 6) là : y - y0 = f '(x0) ( x - x0 )
thay các số liệu vào ta thu được : y - 6 = 0
-Giải câu 2a .
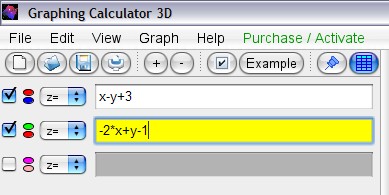
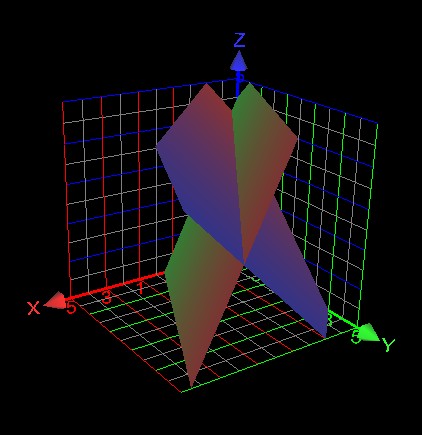
-Dùng Graphing Package vẽ đồ thị ( xem hình sau ) .
-Để ý rằng đồ thị hàm số có tiêm cận đứng x = 1/2 .
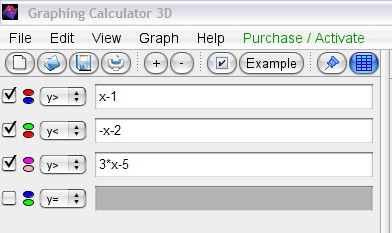
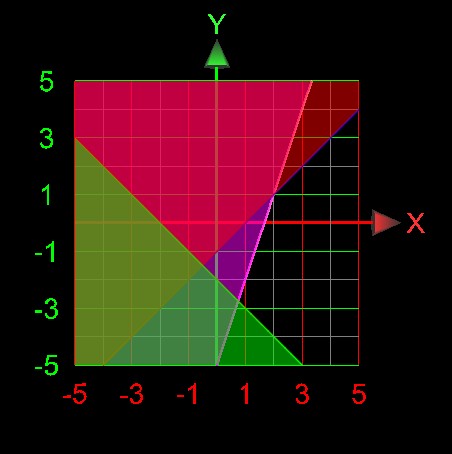
-Đưa đoạn [ -2 , 0 ] vào đồ thị , xoá phần bên ngoài , ta sẽ tìm giá trị lớn nhất , nhỏ nhất trên phần còn lại ( xem hình sau )
-Dùng Mathway để tìm Maximum và Minimum ,
-Phần tính toán của Mathway có lỗi sai khi kết luận x = 1 là cực tiểu địa phương ( Điều kiện có nghĩa của hàm số y = x^2 - ln( 1 - 2x ) là 1 - 2x > 0 <=> x < 1/2 nên x = 1 không thuộc tập xác định của hàm số này )
-Tính các giá trị của hàm số tại các điểm : x = -2 ; x = -1/2 ; x = 0
-Ở phần này Mathway không hiển thị kết quả symbolic cho các giá trị của hàm số ở các hoành độ tương ứng ( xem hình vẽ )
-Sử dụng công cụ trên http://cohtrantmed.yolasite.com/widgets-truc-tuyen.php
phần D10.8 Tính giá trị biểu thức hàm số , ta có :
f(-2) =
f(-1/2) =
f(0) = 0
-Như vậy Max y [-2,0] = ; Min y [-2,0] =
; Min y [-2,0] = 
f(-2) =
f(-1/2) =
f(0) = 0
-Như vậy Max y [-2,0] =
| -Xem hình mô tả sử dụng Mathematica |
|---|
|
** Nhận xét : |
|---|
| Thực tế chỉ ra rằng Mathway có khá nhiều lỗi cơ bản , ví dụ : tìm GTLN , GTNN , Cực đại , cực tiểu , khi tính giá trị biểu thức không cho ra kết quả numeric lẫn symbolic . |
|---|
| Ví dụ : tìm cực trị địa phương của hàm số y = x^3 - 3x^2 - 9x + 1 là có lỗi sai về kết quả Cực đại địa phương ; |
|---|
| Ví dụ : Tìm GTLN , GTNN của y = x^2 - ln ( 1 - 2x ) ; |
|---|
| Ví dụ : Tìm giá trị của hàm số này tại x = 0 , x = -2 , x = -1/2 đều không ra kết quả cụ thể | ||||||
|---|---|---|---|---|---|---|
Chú thích : bản đề nghị hiệu chỉnh của tác giả gửi cho Mathway .
====================================================================
Hello Mathway ,
I've found an important error in your program about the Applications of Differentiation to find the Local Maxima and Minima of the function y = f(x) = x^2 - ln ( 1 - 2*x ) .
Your result shows that x = 1 is a local minimum and here is a basic wrong .
1. First of doing math on the function we must find the reasonable condition for what we will do next . In this case , we have to solve the inequality : 1 - 2x > 0 for x . Thus x < 1/2 and the domain of the function is D = (-infinity , 1/2 ) .
2. When we compute the derivative of f(x) and solve the equation f ' (x) = 0 for x ( critical values ) we must compare each solution to the reasonable condition of the function given .
For instance : f ' (x) = 0 <=> 2*x + 2/( 1 - 2*x ) = 0 <=> x = -1/2 (accepted) V x = 1 (rejected) .
3. We also find the limitation of the function as x tends to x0 ( the value we cancelled because of violation to the domain of the function given , if exist ) . The limit [ x^2 - ln ( 1 - 2*x )] as x -> 1/2(-) { i.e x < 1/2 } tends to + infinity , so the limit [ x^2 - ln ( 1 - 2*x )] as x -> 1 does not exist . This is not local extremum of f(x) .
4. The function y = f(x) = x^2 - ln ( 1 - 2*x ) has a vertical asymptote x = 1/2 , its graph shows that the local maximum does not exist . Also notice the graph of this function can not appear on your worksheet .
Hope see your reply ,
Best Regards ,
Co.H.Tran
====================================================================
--------------------------------------------------------------------------------------------
Chúng ta sẽ tiếp tục giải các bài toán ở phần 3 .
Trần hồng Cơ ,
18/04/2012
==============================================================
Chú thích : tác giả vừa nhận được thư phúc đáp của Mathway .
RE: Mathway Support




Date:
Fri, Apr 20, 2012 12:19 am
_____________________________________________________________________
Hello, Thanks for contacting us. The development team is working on an update to resolve this issue for you. The next Mathway update is scheduled to be released in a few days. Thanks again, please let us know if you have any additional questions. Sincerely, The Mathway Team -----Original Message-----
Name*: Co.H.Tran Email*: cohtran@aol.com Subject*: Additional for Mathway worksheet . Message*: Hello Mathway , I've found an important error in your program about the Applications of Differentiation to find the Local Maxima and Minima of the function y = f(x) = x^2 - ln ( 1 - 2*x ) . Your result shows that x = 1 is a local minimum and here is a basic wrong . 1. First of doing math on the function we must find the reasonable condition for what we will do next . In this case , we have to solve the inequality : 1 - 2x > 0 for x . Thus x < 1/2 and the domain of the function is D = (-infinity , 1/2 ) . 2. When we compute the derivative of f(x) and solve the equation f ' (x) = 0 for x ( critical values ) we must compare each solution to the reasonable condition of the function given . For instance : f ' (x) = 0 <=> 2*x + 2/( 1 - 2*x ) = 0 <=> x = -1/2 (accepted) V x = 1 (rejected) . 3. We also find the limitation of the function as x tends to x0 ( the value we cancelled because of violation to the domain of the function given , if exist ) . The limit [ x^2 - ln ( 1 - 2*x )] as x -> 1/2(-) { i.e x < 1/2 } tends to + infinity , so the limit [ x^2 - ln ( 1 - 2*x )] as x -> 1 does not exist . This is not local extremum of f(x) . 4. The function y = f(x) = x^2 - ln ( 1 - 2*x ) has a vertical asymptote x = 1/2 , its graph shows that the local maximum does not exist . Also notice the graph of this function can not appear on your worksheet . Hope see your reply , Best Regards , Co.H.Tran
==============================================================
Giới thiệu : Thân mời các bạn xem qua bài viết sau
MỘT CÔNG CỤ TÍNH TOÁN TRỰC TUYẾN KHÁ TỐT .
--------------------------------------------------------------------------------------------------------------
Encalc The Free Online Scientific Calculator
Học toán nhiều cũng hơi mệt , chúng ta hãy giải trí với bộ phim
=================================================================
------------------------------------------------------------------------------------------------------------------
Chúng ta phải biết và chúng ta sẽ biết .