KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D -
Phần 3 . As - Co (1-10)

Lời nói đầu .
Như chúng ta đã biết loạt bài " DANH MỤC CÁC ĐƯỜNG CONG " được trình bày trước đây gồm có 3 phần . Nội dung của những phần này là liệt kê các phương trình , tên gọi cùng các giai thoại và chú thích lịch sử của một số đường cong thường xuất hiện trong toán học , vật lý , thiên văn và nhiều ngành kỹ thuật khác .
Bạn đọc có thể theo dõi chi tiết trên các trang sau :
Phần 3 .
http://cohtran.blogspot.com/2012/09/danh-muc-cac-duong-cong-3.
Phiên bản mới nhất đăng trên
http://tusach.thuvienkhoahoc.com/wiki/Danh_mục_và_lịch_sử_các_đường_cong
Tiếp theo sau đây là chuyên mục " KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D " ,
Mục đích của chuỗi bài viết này là khảo sát đồ thị các đường cong bằng các công cụ trực tuyến (online) hoặc trình ứng dụng ( phần mềm offline ) .
Việc thực hành này là hết sức cần thiết và cũng mang lại nhiều kết quả lợi ích . Một mặt nó giúp chúng ta hiểu rõ hơn về các tính chất đặc trưng của các đường cong , mặt khác cũng là dịp làm quen với một số trình ứng dụng có quy mô lớn và tốc độ xử lý rất mạnh . Từ đó chúng ta có thêm kiến thức về đồ họa phục vụ cho việc nghiên cứu hoặc giải quyết những bài toán cụ thể trong phạm vi chuyên môn của mình .
Xin trân trọng giới thiệu cùng bạn đọc .
Trần hồng Cơ
Ngày 28 /04/ 2014 .
-----------------------------------------------------------------------------------------------------------------------------------
Chào các bạn , thế là chúng ta đã cùng nhau bước qua những khó khăn để tìm hiểu một chút về đồ họa các đường cong . Nhà toán học David Hilbert cũng đã từng phán quyết rằng : " Chúng ta phải biết , và chúng ta sẽ biết " trong lúc bàn thảo về những trở ngại trong quá trình tư duy lý luận .
Đúng vậy , khi đã có thông tin khá đầy đủ về trình ứng dụng và công cụ trực tuyến , chắc chắn rằng mọi việc sẽ được giải quyết ổn thỏa trong bài viết này : kỹ thuật đồ họa 2D cho những hàm số , biểu thức , phương trình biểu diễn các đường cong mà chúng ta đã từng biết đến trước đó .
Về thứ tự trình bày bạn đọc có thể theo dõi loạt bài " DANH MỤC CÁC ĐƯỜNG CONG " .
Lưu ý rằng trong các tiểu mục dưới đây phần nhập liệu gồm các toán tử dùng cho các trình hoặc công cụ để phác họa đồ thị .
I . Vẽ đồ thị các đường cong từ As - Ca [ 1 - 5 ] bằng trình ứng dụng .
1.1. Astroid [1] .


A. Khái niệm .
Astroid được hình thành bằng cách lăn một vòng tròn bán kính a / 4 ( hoặc 3a / 4 ) bên trong một vòng tròn có bán kính a. Không mất tính tổng quát ta có thể giả sử a = 1 , phương trình tham số của astroid là
$x = cos^3 t , y = sin^3 t$ từ đó $\ x^{2/3} + y^{2/3} = cos^2t+sin^2t = 1$
Mặt khác vì $sin^6t + cos^6t = 1 - 3.sin^2t.cos^2t$ nên $sin^6t + cos^6t - 1 = - 3.sin^2t.cos^2t$
Lũy thừa 3 cho hai vế $(sin^6t + cos^6t - 1)^3 = - 27.sin^6t.cos^6t$
Hay $(sin^6t + cos^6t - 1)^3 + 27.sin^6t.cos^6t = 0$ trả về x , y ta có
$(x^2 + y^2 - 1)^3 + 27.x^2y^2 = 0$
Do đó astroid có bậc 6 , nó có 4 điểm kỳ dị tại 4 đỉnh trong mặt phẳng thực , hai điểm kỳ dị phức ở vô cực và 4 điểm đôi phức , tổng cộng là 10 điểm kỳ dị .
Đổi sang tọa độ cực , phương trình đường cong astroid là $r=\left | sect \right |/(1+tan^{2/3}t)^{3/2} $
+Chiều dài cung $L(t)=3/2 . sin^2t ( 0< t < \pi/2)$
+Độ cong $C(t)=-2/3 |csc(2t)| $
+Chu vi $P=6a$
+Diện tích $S=3\pi a^2/8$ hay $S \approx 1.178 a^2 $
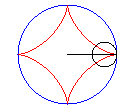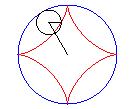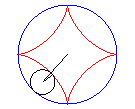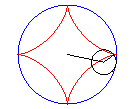


Các đường liên hợp :
Xem
http://youtu.be/CZzazxrRURw
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes :
$\ x^{2/3} + y^{2/3} = a^{2/3}$
Nhập liệu : x^(2/3) + y^(2/3) = a^(2/3)
Phương trình đường cong dạng tham số :
$x = acos^3 t , y = asin^3 t$
Nhập liệu : x = a*cos(t)^3 , y = a*sin(t)^3
Chọn a = 3 .
Khi đó : $x^{2/3} + y^{2/3} = 3^{2/3}$
Nhập liệu : x^(2/3) + y^(2/3) = 3^(2/3)
hoặc $x = 3cos^3 t , y = 3sin^3 t$
Nhập liệu : x = 3*cos(t)^3 , y = 3*sin(t)^3
1.1.1 GP - GC - GX Astroid .
Nguồn :
http://youtu.be/tgzXWk3F4BA
1.1.2 wxM - MAPLE V Astroid .
Nguồn :
http://youtu.be/QB2Do4IjLWs
Nhận xét :
GP : Nhập liệu 2 dạng : ẩn ( implicit ) và tham số (parameter) .
GC : Nhập liệu dạng tham số .
GX : Nhập liệu dạng tham số .
wxM : Nhập liệu dạng tham số .
Maple V : Nhập liệu dạng ẩn ( chỉ vẽ phần đồ thị ở miền 1/4 thứ nhất ) hoặc dạng tham số .
Lưu trữ : http://yadi.sk/d/okf1hhx7P4rTt
1.2 Bicorn (đường mào gà) [2] .
A. Khái niệm .
Đường mào gà bicorn được hình thành như sau :
[ theo Charlotte Scott, 1896 ] Cho 2 đường tròn bằng nhau (C) và (C') tiếp xúc ngoài . Điểm N chạy trên (C') , dựng đường tròn (C") có đường kính ON . Quỹ tích giao điểm M giữa trục đẳng phương của (C) và (C") và đường thẳng kẻ từ N song song với OO' là đường bicorn .
[ theo G. de Longchamps, 1897 ] Cho điểm A(a,0) và B(-a,0) và đường tròn (C) tâm C(0,b) có bán kính là c . Điềm P chạy trên (C) khi đó quỹ tích trực tâm H của tam giác ABP có dạng tham số
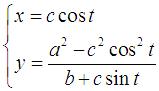
với
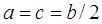
quỹ tích H là đường bicorn
+Chiều dài cung $L(\theta) \approx 5.056a$
+Độ cong
$C[\theta]=6 \sqrt{2} (cost -2 )^3(3cost - 2 )sect / [a(73-80cost +9cos2t )^{3/2}]$
+Chu vi
+Diện tích $S=1/3 . (16\sqrt{3}-27)\pi a^2$
Các đường liên hợp
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y^2.(a^2− x^2) = (x^2 + 2ay − a^2)^2$
Nhập liệu : y^2*(a^2− x^2) = (x^2 + 2*a*y − a^2)^2
Chọn a = 3
Khi đó : $y^2(9− x^2) = (x^2 + 6y − 9)^2$
Nhập liệu : y^2*(9− x^2) = (x^2 + 6*y − 3^2)^2
Phương trình tham số đường cong trong hệ tọa độ Descartes:
$x=a.sint , y = acos^2t .( 2+cost)/(3+sin^2t)$
1.2.1 GP - GC - GX Bicorn .
Nguồn :
http://youtu.be/NnYJV3bgjoA
1.2.2 wxM - MAPLE V Bicorn .
Nguồn :
http://youtu.be/yjBhQE4faTI
Nhận xét :
GP : Nhập liệu dạng ẩn .
GC : Nhập liệu dạng hàm thông thường y = f(x) ( nhờ Maple V giải tìm y rồi nhập 2 lần ) .
GX : Nhập liệu dạng ẩn .
wxM : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
Maple V : Nhập liệu dạng ẩn ( đồ thị này cần điều chỉnh ) hoặc dạng thông thường (nên nhập dạng này ) .
1.3 Cardioid (đường hình tim) [3] .
A. Khái niệm .
Cardioid là quỹ tích của một điểm trên chu vi của đường tròn lăn không trượt trên chu vi của một đường tròn khác có cùng bán kính.
Dựa trên mô tả của đường tròn chuyển động , trong đó đường tròn cố định có tâm tại gốc tọa độ và cả hai có cùng bán kính , phương trình tham số của cardioid là
$x = a(2cost-cos2t)$
$y = a(2sint-sin2t)$
Trong mặt phẳng phức ta có
$z = a(2e^{it}-e^{2it})$
Có thể kiểm tra dễ dàng rằng $(z\overline{z}-a^2)^2=4a^2(z-a)(\overline{z}-a)$
hay
$(x^2+y^2-a^2)^2=4a^2((x-a)^2+y^2)$
Đổi trục $X = x - a , Y = y$ và sau đó thay $X = x , Y =y $ ta thu được
$(x^2+y^2-2ax)^2=4a^2(x^2+y^2)$
+Chiều dài cung $L(\theta) = 8asin^2(t/4)$
+Độ cong
$C[\theta]=\frac{3}{4a} csc(t /2) $
+Chu vi $P=8a$
+Diện tích $S=\frac{3}{2} \pi a^2$
Các đường liên hợp
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes
$4a^2(x^2 + y^2) = (x^2 + y^2 - 2ax)^2$
Nhập liệu : 4*a^2*(x^2 + y^2) = (x^2 + y^2 - 2*a*x)^2
Phương trình đường cong trong tọa độ cực:
$r = 2a(1 + cosθ)$
Nhập liệu : r = 2*a*(1 + cos(θ))
Chọn a = 3
Khi đó : $36(x^2 + y^2) = (x^2 + y^2 - 6x)^2$
Nhập liệu : 36*(x^2 + y^2) = (x^2 + y^2 - 6*x)^2
hoặc
$r = 6(1 + cosθ)$
Nhập liệu : r = 6*(1 + cos(θ))
1.3.1 GP - GC - GX Cardioid .
Nguồn :
http://youtu.be/PnquQ2WzRcc
1.3.2 wxM - MAPLE V Cardioid .
Nguồn :
http://youtu.be/fFujCHvbDMs
Nhận xét :
GP : Nhập liệu dạng thường r = f(θ) .
GC : Nhập liệu dạng hàm tọa độ cực r = f(θ) .
GX : Nhập liệu dạng hàm tọa độ cực .
wxM : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
Maple V : Nhập liệu dạng ẩn ( đồ thị này cần điều chỉnh ) hoặc dạng thông thường (nên nhập dạng này ) .
Lưu trữ : http://yadi.sk/d/1ywU88FuP4sBm
1.4 Cartesian Oval (đường oval Descartes) [4] .
A. Khái niệm .
Đường cong Cartesian bao gồm 2 đường oval lồng nhau, là quỹ tích của một điểm P có khoảng cách là s và t từ hai điểm cố định S và T thỏa mãn: s + mt = a .
Khi c là khoảng cách giữa S và T phương trình đường cong có biểu diễn như sau
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$[(1 - m^2)(x^2 + y^2) + 2m^2cx + a^2 - m^2c^2]^2 = 4a^2(x^2 + y^2)$
Nhập liệu : ((1 - m^2)*(x^2 + y^2) + 2*m^2*c*x + a^2 - m^2*c^2)^2 = 4*a^2*(x^2 + y^2)
chọn m=2 , a=2 , c=3
Khi đó : $(-3x^2-3y^2+24x-32)^2 = 16x^2+16y^2$
Nhập liệu : (-3*x^2-3*y^2+24*x-32)^2 = 16*x^2+16*y^2
1.4.1 GP - GC - GX Cartesian Oval .
Nguồn :
http://youtu.be/mokHE7fytZo
1.4.2 wxM - MAPLE V Cartesian Oval .
Nguồn :
http://youtu.be/QWjTh7sdhZA
Nhận xét :
GP : Nhập liệu dạng ẩn .
GC : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
GX : Nhập liệu dạng hàm ẩn .
wxM : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
Maple V : Nhập liệu dạng ẩn ( đồ thị này cần điều chỉnh ) hoặc dạng thông thường (nên nhập dạng này ) .
1.5 Cassinian Ovals (đường oval Cassini) [5] .
A. Khái niệm .
Cassinian Ovals là quỹ tích của một điểm P di chuyển sao cho tích của 2 khoảng cách từ P đến hai điểm cố định S và T [ trong trường hợp này điểm

] là một hằng số. Hình dạng của đường cong phụ thuộc vào tỷ số c / a
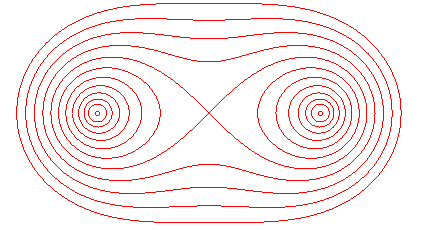
Nếu c > a thì đường cong bao gồm hai vòng.
Nếu c < a đường cong bao gồm một vòng đơn.
Nếu c = a đường cong có dạng Lemniscate Bernoulli (là một trong tám đường cong kiểu mẫu giới thiệu bởi Jacob Bernoulli).
- Một dạng khác của phương trình đường cong Cassini trong hệ tọa độ Descartes
$(x^2+y^2+a^2)^2=4a^2x^2+b^4$
Khi $a<b$
+Diện tích $S= a^2+b^2 E(a^2/b^2) $ Với $E(k)$ là tích phân Elliptic loại 2 .
Khi $a=b$
+Diện tích $S=2. a^2 $
Phương trình dạng ẩn trong hệ tọa độ cực
$r^2=a^2.[cos2\theta + \sqrt{b^4/a^4-sin^2\theta}]$
$r^2=a^2.[cos2\theta - \sqrt{b^4/a^4-sin^2\theta}]$
Với $\theta \in [-1/2.arcsin(b^2/a^2) , 1/2.arcsin(b^2/a^2) ]$
Các tính chất khác
Xem
http://youtu.be/NFqFh5qyZUE
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$(x^2 + y^2)^2 - 2a^2(x^2 - y^2) = c^4 - a^4$
Nhập liệu : (x^2 + y^2)^2 - 2*a^2*(x^2 - y^2) = c^4 - a^4
chọn a=3 , c=2
Khi đó : $(x^2+y^2)^2-18x^2+18y^2 = -65$
Nhập liệu : (x^2+y^2)^2-18*x^2+18*y^2 = -65
1.5.1 GP - GC - GX Cassinian Ovals .
Nguồn :
http://youtu.be/8QTOjFBw4DE
1.5.2 wxM - MAPLE V Cassinian Ovals .
Nguồn :
http://youtu.be/WqwIvF557cs
Nhận xét :
GP : Nhập liệu dạng ẩn .
GC : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
GX : Nhập liệu dạng hàm ẩn .
wxM : Nhập liệu dạng thông thường y = f(x) ( nhờ Maple V giải tìm y ) .
Maple V : Nhập liệu dạng ẩn (nên nhập dạng này ) hoặc dạng thông thường ( đồ thị này cần điều chỉnh ) ./
Lưu trữ : http://yadi.sk/d/V4MQreciP4sbR
II . Vẽ đồ thị các đường cong từ Ca - Co [ 6 - 10 } bằng công cụ trực tuyến .
Điểm cần lưu ý khi chúng ta dùng các websites để minh họa đồ thị các đường cong là đường truyền Internet phải tương đối mạnh , cấu hình máy tính phải phù hợp theo yêu cầu và được cài đặt nền Java . Ngoài ra các bạn cũng nên có sẵn một trình chụp màn hình nếu không thể download hoặc save hình ảnh vừa tạo . ( Có thể dùng Irfan View Portable - Click và download về máy
http://portableapps.com/IrfanViewPortable4.3.7 hoặc
https://drive.google.com/file/d/0B7rE-PgbIuIpZFNobDZaRklQYUE/edit?usp=sharing )
2.1 Catenary (đường dây xích) [6] .
A. Khái niệm .
Đường cong Catenary hình thành bởi một dây nặng đồng chất lý tưởng treo tự do từ hai điểm cố định . Điểm thấp nhất A (xem hình minh họa) là đỉnh. Phần AP ở trạng thái cân bằng dưới sức căng ngang H tại A, sức căng F hướng dọc theo tiếp tuyến tại P, và AP có trọng lượng W. Nếu trọng lượng của chuỗi w trên đơn vị chiều dài và s là cung AP, ta có W = ws; và từ tam giác lực thì $tan ψ = ws / H = s / a$ , trong đó
$a = H / w$ được gọi là tham số của dây xích. Do đó, dây xích có phương trình vi phân biểu diễn là
+Chiều dài cung $L(x) = a.sinh(x /a)$
+Độ cong $C(t) = \frac{1}{a} sech^2(x /a) $
+Chu vi
+Diện tích
Các đường liên hợp
Xem
http://youtu.be/eo8CGRLlFks
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y = a.cosh(x/a)$
Nhập liệu : y =a* cosh(x/a)
Chọn a = 2
Khi đó : $y = 2cosh(x/2)$
Nhập liệu : y = 2*cosh(x/2)
2.1.1 WA - Desmos (DE) - Seriesmathstudy (SMS) Catenary .
Xem phần 1.II.2.1.2
Đường dẫn :
http://www.wolframalpha.com/widgets/plotter
Xem phần 1.II.2.2 và 2.3
Nguồn :
http://youtu.be/dlYSDdvZArk
2.1.2 Flash&Math (FM) - MathsTools (MT) - FooPlot (FP) Catenary .
Xem phần 1.II.2.4 , 2.5 và 2.6
Nguồn :
http://youtu.be/YMB4FXgHkL8
Nhận xét :
WA : Nhập liệu dạng thông thường y = f(x) .
DE : Nhập liệu dạng thông thường y = f(x) ( có chức năng vẽ họ đường cong ) .
SMS : Nhập liệu dạng thông thường y = f(x) ( có chức năng vẽ đường cong 3D ) .
FM : Nhập liệu dạng tham số x(t) = t , y(t) = f(x(t))
MT : Nhập liệu dạng thông thường y = f(x) .
FP : Nhập liệu dạng thông thường y = f(x) .
Lưu trữ : http://yadi.sk/d/ek_0YhfsP4soq
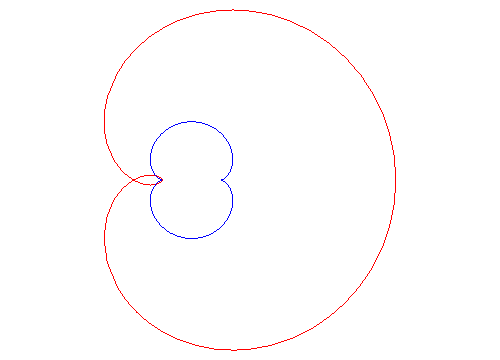
2.2 Cayley's sextic (đường bậc 6 Cayley) [7] .
A. Khái niệm .
Sextic Cayley được tạo bằng cách quay các tiếp tuyến của cardioid từ đỉnh của nó (ở đây là cardioid
$ r = a.cos^2( \theta)$ ) ( xem hình )
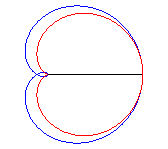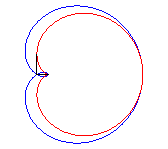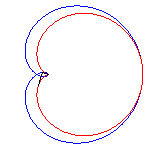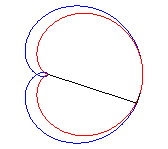
Sextic Cayley cũng là néphroïde được phát triển ra có tâm ( a / 2, 0) và đi qua gốc O.
Sextic Cayley cũng là đường cong ngược của đường bậc 3 Tschirnhausen

Phương trình tham số đường cong trong hệ tọa độ Descartes:
$x=4a.cos^3(t/3).cost , y =4a.cos^3(t/3).sint$
+Chiều dài cung $L(t) = [2t+3.sin(2t /3)]a$ với $t \in (0,3 \pi)$
+Độ cong $C(t)=\frac{4}{3a} sec^2(t /3) $
+Chu vi $P = 6 \pi a$
+Diện tích giới hạn bởi biên ngoài $S=(5\pi + 9/2. \sqrt{3}).a^2)$ hay $S \approx 23.502 a^2$
Diện tích vòng loop $S_{loop} = 1/2.(5\pi - 9/2. \sqrt{3}).a^2$ hay $S_{loop} \approx 0.059.a^2$
Các đường liên hợp
Xem
http://youtu.be/1EZjzkus95o
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$4(x^2 + y^2 - ax)^3 = 27a^2(x^2 + y^2)^2$
Nhập liệu : 4*(x^2 + y^2 - a*x)^3 = 27*a^2*(x^2 + y^2)^2
Phương trình đường cong trong hệ tọa độ cực:
$r =4acos^3(\theta/3)$
Nhập liệu : r =4*a*cos(theta/3)^3
Chọn a = 2 .
Khi đó : $4(x^2+y^2-2x)^3 = 108(x^2+y^2)^2$
Nhập liệu : 4*(x^2+y^2-2*x)^3 = 108*(x^2+y^2)^2
hoặc
$r =8cos^3( \theta/3)$
Nhập liệu : r =4*2*cos(theta/3)^3
2.2.1 WA - Desmos (DE) - Seriesmathstudy (SMS) - Flash&Math (FM) Cayley's Sextic .
Nguồn :
http://youtu.be/B724uHrjoc8
2.2.2 Flash&Math (FM) - MathsTools (MT) - FooPlot (FP) Cayley's Sextic .
Nguồn :
http://youtu.be/cIyx46sbI1c
Nhận xét :
WA : Nhập liệu dạng hàm ẩn 2.1.9 .
DE : Nhập liệu dạng hàm ẩn ( có chức năng vẽ họ đường cong , rất tốt ) .
SMS : Nhập liệu dạng thông thường y = f(x) ( Hình không chuẩn , không nên dùng ) ./
FM : Nhập liệu hàm ẩn .
MT : không nhập được ( Không nên dùng ) ./
FP : Nhập liệu dạng hàm tọa độ cực r = f(θ) .
Lưu trữ : http://yadi.sk/d/aAy7TcvjP4svi
2.3 Circle (đường tròn) [8] .
A. Khái niệm .
Phương trình đường cong trong hệ tọa độ Descartes: Đường tròn là tập hợp các điểm chuyển động luôn cách đều một điểm cố định ( gọi là tâm ) một đoạn không đổi ( gọi là bán kính - ký hiệu R ) .
Gọi I(a,b) là tâm đường tròn , vì IM = R nên $\sqrt{(x-a)^2+(y-b)^2}=R$ hay $(x-a)^2+(y-b)^2=R^2$
Khi I(a,b) trùng với gốc tọa độ O(0,0) ta có $x^2 + y^2 = R^2$
Phương trình đường cong tham số:
$x = Rcost , y = Rsint$
+Chiều dài cung $L(t) = R.t$
+Độ cong $C(t)=\frac{1}{R}$
+Chu vi $ P=2\pi R$
+Diện tích $S= \pi R^2$
Các đường liên hợp
Xem
http://youtu.be/w4wAsHkdI2Y
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$x^2 + y^2 = R^2$
Nhập liệu : x^2 + y^2 = R^2
Phương trình đường cong tham số:
$x = Rcost , y = Rsint$
Nhập liệu : x = R*cos(t) , y = R*sin(t)
Phương trình đường cong trong hệ tọa độ cực:
r = R
Chọn R = 1 .
Khi đó $x^2 + y^2 = 1$
Nhập liệu : x^2 + y^2 = 1
hoặc
Nhập liệu : x = cos(t) , y = sin(t)
r = 1
2.3.1 WA - Desmos (DE) - Seriesmathstudy (SMS) Circle .
Nguồn :
http://youtu.be/JhXm8G0TeTA
2.3.2 Flash&Math (FM) - MathsTools (MT) - FooPlot (FP) Circle .
Nguồn :
http://youtu.be/d327el298mk
Nhận xét :
WA : Nhập liệu dạng tham số 2.1.6 .
DE : Nhập liệu dạng hàm ẩn .
SMS : Nhập liệu dạng tham số .
FM : Nhập liệu hàm ẩn .
MT : Nhập liệu dạng tham số ( Hình không chuẩn , không nên dùng ) ./
FP : Nhập liệu dạng tham số .
Lưu trữ : http://yadi.sk/d/7QO1sk7xP57cf
2.4 Cissoid of Diocles (đường cissoid Diocles) [9]
 A. Khái niệm .
A. Khái niệm .
Đường tròn (C) có bán kính a , tâm là (a,0) . Khi đó điểm A(2a,0) , gọi M
2 thuộc tiếp tuyến với (C) tại A và tia OM
2 cắt (C) tại điểm M
1 . Khoảng cách từ O đến Cissoid là OM = OM
2 - OM
1 = $2asecθ - 2cosθ$ = $2a sin^2θ / cosθ = 2a sinθ. tanθ$
Đặt $ t = tanθ$
Vì $x = rcosθ , y = tx$ có thể biến đổi thành
$x = rcosθ = {2a sin^2θ / cosθ} . cosθ = 2sin^2θ =$
$= 2a tan^2θ/sec^2θ = 2at^2/(1+t^2)$
$y = tx = 2at^3/(1+t^2)$
Khử t giữa x và y ta thu được $y^2=x^3/(2a-x)$
Phương trình tham số đường cong trong hệ tọa độ Descartes
$x=2at^2/(1+t^2)$
$y=2at^3/(1+t^2)$
Với $ a>0 , t>0$
+Chiều dài cung $L(t) =a.[\sqrt{3}.ln2 - 4 + 2\sqrt{3}.ln(2+ \sqrt{3}) - 2 \sqrt{3}.ln(\sqrt{6}cost + \sqrt{5+3.cos2t})+sect . \sqrt{10+6.cos2t} ]$
+Độ cong $C(t) = \frac{3.tan^2t}{a.(sec^4t+2.sec^2t -3)^{3/2}}$
+Chu vi
+Diện tích giới hạn bởi đường cong và tiệm cận $S=3 \pi a^2$
Với $ a>0 , t \in ( - \pi/2 , \pi /2 )$
+Chiều dài cung $L(t) = 2a.[ \sqrt{t^2+4}-2+\sqrt{3}.arctan(2/ \sqrt{3}) - \sqrt{3}.arctan \sqrt{(t^2 +4)/3} ]$
+Độ cong $C(t)=\frac{3}{a.|t|.(4+t^2)^{3/2}}$
+Chu vi
+Diện tích giới hạn bởi đường cong và tiệm cận $S=3 \pi a^2$
Các đường liên hợp
Xem
http://youtu.be/Wn-39tWDQJI
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y^2=x^3/(2a-x)$
Nhập liệu : y^2=x^3/(2*a-x)
Phương trình đường cong trong hệ tọa độ cực:
$r = 2a. tanθ.sinθ$
Nhập liệu : r = 2*a*tan(θ)*sin(θ)
Chọn a = 2
Khi đó $y^2=x^3/(4-x)$
Nhập liệu : y^2=x^3/(2*2-x)
hoặc
$r = 4tanθ. sinθ$
Nhập liệu : r = 2*2*tan(θ)*sin(θ)
2.4.1 WA - Desmos (DE) - Seriesmathstudy (SMS) Cissoid of Diocles .
Nguồn :
http://youtu.be/q4ZJENsALho
2.4.2 Flash&Math (FM) - MathsTools (MT) - FooPlot (FP) Cissoid of Diocles .
Nguồn :
http://youtu.be/LKD6c9zU76o
Nhận xét :
WA : Nhập liệu dạng hàm tọa độ cực 2.1.4 .
DE : Nhập liệu dạng hàm tọa độ cực .
SMS : Nhập liệu dạng hàm tọa độ cực .
FM : Nhập liệu dạng tham số tọa độ cực .
MT : Nhập liệu dạng tham số ( Hình không chuẩn , không nên dùng ) ./
FP : Nhập liệu dạng hàm tọa độ cực .
Lưu trữ : http://yadi.sk/d/ByIEzLaRPGQYD
2.5 Cochleoid (đường ốc sên Cochleoid) [10]
A. Khái niệm .
Cochleoid là quỹ tích các điểm cuối của một cung có độ dài cố định với đầu kia và luôn được gắn chặt vào một đường thẳng tiếp xúc cố định nằm ngang . Người ta có thể tưởng tượng trong thực tế đường cong mô tả bằng đoạn cuối của một ống nhựa cuộn theo một hình tròn, mà đầu kia là cố định. Cochleoid có vô hạn các xoắn ốc, đi qua cực của nó và tiếp xúc với trục cực nằm ngang . Cực là một điểm kỳ dị đa vô hạn. Bất kỳ đường thẳng qua O đều cắt cochleoid; các tiếp tuyến với cochleoid tại các giao điểm này đều đi qua cùng một điểm.
Phương trình tham số đường cong :
$x = asin2t/{2t}$
$y = asin^2t/t$
+Chiều dài cung
+Độ cong $C(t)=\frac{2\sqrt{2}.t^3.(2t - sin2t )}{(1+2t^2 - cos2t - 2t .sin2t )^{3/2}} $
+Chu vi
+Diện tích
Các đường liên hợp
Xem
http://youtu.be/f5fM9dZDB8c

B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes
$(x^2+y^2)arctan(y/x) = ay$
Phương trình tham số đường cong :
$x = asin2t/{2t}$
$y = asin^2t/t$
Phương trình đường cong trong hệ tọa độ cực:
$r = a sinθ/θ$
Nhập liệu : r = a sin(θ)/θ
Chọn a = 1
Khi đó r = sin(θ)/θ
2.5.1 WA - Desmos (DE) - Seriesmathstudy (SMS) Cochleoid .
Nguồn :
http://youtu.be/gKWCOat1tiY
2.5.2 Flash&Math (FM) - MathsTools (MT) - FooPlot (FP) Cochleoid .
Nguồn :
http://youtu.be/4GYQwhXUlAw
Nhận xét :
WA : Nhập liệu dạng hàm tọa độ cực .
DE : Nhập liệu dạng hàm tọa độ cực .
SMS : Nhập liệu dạng hàm tọa độ cực .
FM : Nhập liệu dạng tham số tọa độ cực .
MT : Nhập liệu dạng tham số ( Hình không chuẩn , không nên dùng ) ./
FP : Nhập liệu dạng hàm tọa độ cực .
Lưu trữ : http://yadi.sk/d/5e2RNFEEPMBzu
III . Lời kết .
Đến đây có lẽ bạn đọc đã phần nào quen thuộc với các trình ứng dụng ( GP,GC,GX,wxM ,Maple V) và các công cụ trực tuyến ( WA,DE,SMS,FM,MT,FP ) giúp cho việc khảo sát đồ thị các đường cong với nhập liệu các hàm dạng thông thường , hàm tọa độ cực , hàm ẩn và dạng tham số .
Đặc biệt ở cuối mỗi tiểu mục là phần lưu trữ gồm các files dạng pdf , nb , gif , png , jpg chứa các nội dung liên quan đến đường cong . Tác giả hy vọng rằng những nội dung lưu trữ này sẽ giúp các bạn dễ dàng tìm hiểu thêm và xử lý các thông tin một cách hữu ích .
Trong các bài viết sau ngoải nội dung chính là khảo sát đường cong với các trình ứng dụng và website đồ họa trực tuyến , chúng ta sẽ tìm hiểu thêm về cách nhập liệu biểu thức hàm cho các trình ứng dụng Mathematica , Maple cùng những tùy chọn khi vẽ các đồ thị hàm số .
Cám ơn các bạn đã đọc bài viết này . Hẹn gặp lại .
Trần hồng Cơ
Ngày 05 /05/ 2014 .
-------------------------------------------------------------------------------------------
Khoa học là một điều tuyệt vời khi không phải dùng nó để kiếm sống.
Albert Einstein .




























 ] là một hằng số. Hình dạng của đường cong phụ thuộc vào tỷ số c / a
] là một hằng số. Hình dạng của đường cong phụ thuộc vào tỷ số c / a