Richard Feynman và vật lý học hiện đại .
Bài 2 .

Tiểu sử Richard Feynman - Điện động lực học lượng tử - Tái chuẩn hóa .
Richard Phillips Feynman sinh ra tại Brooklyn (New York) năm 1918 trong một gia đình Do Thái. Richard Feynman tốt nghiệp Học viện kỹ thuật Massachusetts (MIT) vào năm 1939, bảo vệ bằng tiến sỹ tại Đại học Princeton dưới sự hướng dẫn của John Wheeler vào năm 1942. Ngay sau đó, ông bị lôi kéo vào dự án Manhattan. Ở đó, ông nổi tiếng về tính cách cởi mở và hài hước – tại Phòng thí nghiệm Los Alamos, ông rất thích phá các hệ thống bảo mật – và để trở thành một nhà vật lý khác thường: ông trở thành người đóng góp chủ yếu cho lý thuyết bom nguyên tử. Thói quen liên tục tìm tòi khám phá của Feynman về thế giới chính là gốc rễ của con người ông. Nó không chỉ là cái máy làm nên các thành công khoa học mà còn dắt ông đến rất nhiều khám phá kỳ thú ví như giải mã những chữ tượng hình của người Maya. Sau dự án Manhattan, Feynman làm việc cho Đại học Cornell một thời gian trước khi chuyển đến làm việc lâu dài cho Học viện kỹ thuật California (Caltech). Ông không chỉ là một nhà khoa học thiên tài mà còn là một nhà sư phạm tuyệt đỉnh, ông giảng giải các vấn đề vật lý phức tạp cho hầu hết mọi người đều có thể hiểu được.
Vào những năm sau Thế chiến thứ hai, Feynman tìm ra một phương pháp mới rất hiệu quả trong việc nhận thức cơ học lượng tử. Và chính điều đó mang giải Nobel năm 1965 đến với ông. Ông thách thức giả thuyết cổ điển cơ bản là mỗi hạt có một lịch sử đặc biệt. Thay vào đó, ông cho rằng các hạt di chuyển từ nơi này đến nơi khác theo tất cả các lộ trình khả dĩ trong không-thời gian. Mỗi lộ trình Feynman liên hệ với hai con số, con số thứ nhất là kích thước, biên độ của sóng, và con số thứ hai là pha sóng, cho biết đó là đỉnh hoặc hõm sóng (bụng sóng). Xác suất của một hạt đi từ A đến B cho bởi tổng các sóng liên quan đến lộ trình khả dĩ đi qua A và B. Tuy vậy trong cuộc sống hàng ngày, chúng ta thấy dường như các vật thể đi theo một lộ trình duy nhất từ điểm đầu đến điểm cuối. Điều này phù hợp với ý tưởng đa lịch sử (hoặc tổng theo các lịch sử), vì đối với các vật thể lớn thì qui tắc của ông về gán các con số cho mỗi lộ trình đảm bảo tất cả các lộ trình (trừ một lộ trình duy nhất) phải triệt tiêu lẫn nhau khi đóng góp của chúng được kết hợp lại. Chỉ có một trong số vô hạn các lộ trình có ý nghĩa đối với chuyển động của các vật thể vĩ mô là được xem xét và đó chính là lộ trình có được từ các định luật chuyển động cổ điển của Isaac Newton.
Ông còn áp dụng thuyết lượng tử để giải thích tính siêu chảy của helium lỏng và đây là cơ sở cho việc xây dựng lý thuyết siêu dẫn sau này.
Ông còn đưa ra biểu đồ Feynman, rất hữu ích trong việc tính toán tương tác của các hạt trong không-thời gian và là cơ sở của thuyết dây và thuyết M. Năm 1959, Feynman có bài phát biểu nổi tiếng There is a plenty room at the bottom mở ra hướng về công nghệ nanô và được coi là khai sinh ra ngành khoa học và công nghệ nanô.
Sách của Feynman về vật lý
*Elementary Particles and the Laws of Physics : The 1986 Dirac Memorial Lectures
*Six Easy Pieces: Essentials of Physics Explained by Its Most Brilliant Teacher
*Six Not So Easy Pieces: Einstein's Relativity, Symmetry and Space-Time
*The Feynman Lectures on Physics (with Leighton and Sands). 3 volumes 1964, 1966. Library of Congress Catalog Card No. 63-20717
*The Character of Physical Law ISBN 0-262-56003-8
*Quantum Electrodynamics ISBN 0-8053-2501-8
*QED: The Strange Theory of Light and Matter
Statistical Mechanics ISBN 0-8053-2509-3
*Theory of Fundamental Processes ISBN 0-8053-2507-7
*Quantum Mechanics and Path Integrals (with Albert Hibbs) ISBN 0-07-020650-3
*Lectures on Gravitation 1995 ISBN 0-201-62734-5
*Lectures on Computation ISBN 0-201-48991-0
*Feynman's Lost Lecture: The Motion of Planets Around the Sun ISBN 0-09-973621-7
*The Feynman Processor : Quantum Entanglement and the Computing Revolution ISBN 0-7382-0173-1
Sách về Feynman
*Feynman, Richard Phillips. (1999). The Meaning of It All: Thoughts of a Citizen Scientist. Perseus Publishing. (Paperback Edition ISBN 0-7382-0166-9)
*The Pleasure of Finding Things Out
*Surely You're Joking, Mr. Feynman! ISBN 0-393-01921-7
*What Do You Care What Other People Think?
*Genius: The Life and Science of Richard Feynman (by James Gleick)
*Most of the Good Stuff: Memories of Richard Feynman (edited by Laurie M. Brown and John S. Rigden)
*No Ordinary Genius: The Illustrated Richard Feynman (edited by Christopher Sykes)
*Tuva Or Bust! (by Ralph Leighton)
*QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga (Princeton Series in Physics) (by Silvan S. Schweber)
*Selected Papers on Quantum Electrodynamics (Fermi, Jordan, Heisenberg, Dyson, Weisskopf, Lamb, Dirac, Oppenheimer, Retherford, Pauli, Bethe, Bloch, Klein, Schwinger, Tomonaga, Feynman, Wigner, and many others) (by Julian Schwinger (Editor))
*Richard Feynman: A Life in Science (by John Gribbin and Mary Gribbin)
*The Beat of a Different Drum: The Life and Science of Richard Feynman (by Jagdish Mehra)
*Feynman's Rainbow: A Search for Beauty in Physics and in Life (by Leonard Mlodinow) ISBN 0-446-69251-4
*Perfectly Reasonable Deviations from the Beaten Track: The *Letters of Richard P. Feynman - Edited by Michelle Feynman (Basic Books, ISBN 0-7382-0636-9, April 2005).
Xem thêm
Vật lý học
Giải thưởng Nobel về vật lý
Liên kết ngoài
Richard Feynman
*Richard P. Feynman - Nobel Lecture
*Feynman Online!
*Unique freeview videos of Feynman's lectures on QED courtesy of *The Vega Science Trust and The University of Auckland
*Los Alamos National Laboratory Richard Feynman page
The Nobel Prize Winners in Physics 1965
*About Richard Feynman
*Feynman's classic 1959 talk:There's Plenty of Room at the Bottom
*Richard Feynman and The Connection Machine
Infinity tại Internet Movie Database
*PhysicsWeb review of the play QED
*BBC Horizon: The Pleasure of Finding Things Out — with Richard Feynman. A 50-minute documentary interview with Feynman recorded in 1981
*Richard Feynman, Winner of the 1965 Nobel Prize in Physics
Feynman's Scientific Publications
*The Letters of Richard P. Feynman Online
Nguồn : http://vi.wikipedia.org/wiki/Richard_Feynman
*****************************************************************************************************************
Điện động lực học lượng tử
Bách khoa toàn thư mở Wikipedia
Bản mẫu : Lý thuyết trường lượng tử
Trong vật lý hạt, điện động lực học lượng tử (QED) là lý thuyết trường lượng tử tương đối tính của điện động lực học. Về cơ bản, nó miêu tả cách ánh sáng và vật chất tương tác với nhau và là lý thuyết đầu tiên kết hợp được các tính chất của cơ học lượng tử và thuyết tương đối hẹp. QED miêu tả bằng toán học mọi hiện tượng có sự tham gia của các hạt mang điện tương tác với nhau thông qua trao đổi các photon ảo và biểu diễn các tính chất lượng tử của điện từ học cổ điển mang lại một lý thuyết đầy đủ về tương tác vật chất và ánh sáng. Một trong những cha đẻ của QED, Richard Feynman, gọi nó là "viên ngọc của vật lý học" do khả năng tiên đoán chính xác các đại lượng như mômen từ dị thường của electron, dịch chuyển Lamb đối với mức năng lượng của hiđrô.[1]
Theo thuật ngữ kĩ thuật, QED là lý thuyết nhiễu loạn của chân không lượng tử điện từ.
Lịch sử
Lý thuyết lượng tử đầu tiên miêu tả tương tác giữa bức xạ và vật chất do nhà khoa học người Anh Paul Dirac đưa ra, mà (trong thập niên 1920) ông là người đầu tiên tính được hệ số phát xạ tự phát cho một nguyên tử.[2]
 |
| Paul Dirac |
Dirac miêu tả sự lượng tử hóa của trường điện từ giống như các dao động tử điều hòa và giới thiệu khái niệm toán tử sinh và hủy của hạt. Trong những năm sau, với các đóng góp của Wolfgang Pauli, Eugene Wigner, Pascual Jordan, Werner Heisenberg và hình thức điện động lực học lượng tử sáng rõ nêu bởi Enrico Fermi,[3] các nhà vật lý tin rằng, về nguyên lý, có thể tính toán bất kỳ một quá trình vật lý nào có sự tham gia của các photon và các hạt điện tích. Tuy nhiên, những nghiên cứu chi tiết hơn của Felix Bloch và Arnold Nordsieck,[4] và Victor Weisskopf,[5] trong năm 1937 và 1939, cho thấy những tính toán này chỉ tin cậy đối với xấp xỉ bậc nhất của lý thuyết nhiễu loạn, mà Robert Oppenheimer đã chỉ ra trước đó.[6] Những chuỗi vô hạn xuất hiện khi tính đến số hạng bậc cao hơn , khiến cho các tính toán trở lên vô nghĩa và dấy lên những nghi ngờ về tính nhất quán nội tại của lý thuyết. Trong thời gian này chưa có một giải pháp nào được nêu ra, và dường như nó không thể tương thích hoàn toàn đối với cả thuyết tương đối hẹp và cơ học lượng tử.
Những khó khăn trong lý thuyết tăng lên vào cuối thập niên 1940. Với kỹ thuật mới dựa trên sóng vi ba cho phép thực hiện các thí nghiệm đo chính xác hơn mức dịch chuyển năng lượng đối với nguyên tử hiđrô,[7] mà ngày nay gọi là dịch chuyển Lamb và mômen từ dị thường của electron.[8] Những thí nghiệm này cho thấy những giá trị kỳ lạ xuất hiện mà lý thuyết lúc đó không thể giải thích được.
 |
| Hans Bethe |
Hans Bethe là người đầu tiên nêu ra giải pháp khắc phục những trở ngại này. Năm 1947, trên chuyến xe lửa từ New York đến Schenectady,[9] sau khi tham gia hội nghị tổ chức tại Đảo Shelter về chủ đề này, Bethe đã hoàn thành tính toán phi tương đối tính đầu tiên về sự dịch chuyển của các vạch quang phổ của nguyên tử hiđrô mà trước đó Lamb và Retherford đo được.[10] Mặc dù có những hạn chế trong cách tính của ông, kết quả thu được khớp tuyệt vời so với thực nghiệm. Ý tưởng đơn giản nhằm triệt tiêu các giá trị vô hạn để hiệu chỉnh khối lượng và điện tích thu về giá trị hữu hạn như đo bằng các thí nghiệm. Theo cách này, những giá trị vô hạn sinh bởi chuỗi số bị hấp thụ bởi các hằng số và cho kết quả hữu hạn khớp với giá trị đo được từ thí nghiệm. Thủ tục này sau đó gọi là tái chuẩn hóa.
Dựa trên trực giác của Bethe và những bài báo cơ sở về lĩnh vực này của Sin-Itiro Tomonaga,[11] Julian Schwinger,[12][13] Richard Feynman[14][15][16] và Freeman Dyson,[17][18] các nhà vật lý cuối cùng đã có thể tìm ra được những công thức hiệp biến cho giá trị hữu hạn tại bậc xấp xỉ bất kỳ trong chuỗi số miêu tả bằng lý thuyết nhiễu loạn của điện động lực học lượng tử. Sin-Itiro Tomonaga, Julian Schwinger và Richard Feynman cùng nhận giải Nobel Vật lý năm 1965 cho những công trình cơ bản trong ngành này.
 |
| Feynman (giữa) và Oppenheimer (phải) tại Los Alamos. |
[19] Những đóng góp của họ, cùng với của Freeman Dyson, về khuôn khổ lý thuyết hiệp biến và bất biến chuẩn (gauge invariant) của điện động lực học lượng tử cho phép những tính toán về các đại lượng quan sát được tại những bậc xấp xỉ bất kỳ trong lý thuyết nhiễu loạn. Kỹ thuật toán học của Feynman, dựa trên các biểu đồ của ông, ban đầu dường như rất khác lạ so với cách tiếp cận theo lý thuyết trường, và toán tử của Schwinger và Tomonaga, nhưng sau đó Freeman Dyson chứng tỏ rằng hai cách tiếp cận này tương đương với nhau.
[17] Tái chuẩn hóa, sự đòi hỏi gắn các đại lượng vật lý tại những phép phân kỳ nhất định xuất hiện trong lý thuyết thông qua các tích phân, sau đó trở thành một trong những công cụ cơ bản của lý thuyết trường lượng tử và mang lại sự chấp thuận rộng rãi của các nhà vật lý đối với lý thuyết. Ngay cả khi kỹ thuật tái chuẩn hóa hoạt động khá hiệu quả trong thực hành, Feynman không bao giờ cảm thấy dễ chịu hoàn toàn về tính đúng đắn toán học của nó, và ông coi tái chuẩn hóa giống như "trò xóc đĩa" (shell game) và "hocus pocus" (ma thuật).[20]
QED đã trở thành hình mẫu và khuôn khổ cho những lý thuyết trường lượng tử về sau. Một trong những lý thuyết đó là Sắc động lực học lượng tử QCD, hình thành từ đầu thập niên 1960 và có mô hình như ngày nay kể từ những công trình năm 1975 thực hiện bởi H. David Politzer, Sidney Coleman, David Gross và Frank Wilczek. Dựa trên các công trình tiên phong của Schwinger, Gerald Guralnik, Dick Hagen, và Tom Kibble,[21][22] Peter Higgs, Jeffrey Goldstone, và những nhà vật lý khác, Sheldon Glashow, Steven Weinberg và Abdus Salam độc lập với nhau chứng minh được lực hạt nhân yếu và điện động lực học lượng tử có thể thống nhất với nhau thành một lý thuyết chung là lý thuyết lực điện - yếu.
Tham khảo
[1]. Feynman 1985, tr. 6
[2]. P.A.M. Dirac (1927). “The Quantum Theory of the Emission and Absorption of Radiation”. Proceedings of the Royal Society of London A 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
[3] E. Fermi (1932). “Quantum Theory of Radiation”. Reviews of Modern Physics 4: 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
[4] F. Bloch; A. Nordsieck (1937). “Note on the Radiation Field of the Electron”. Physical Review 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
[5] V. F. Weisskopf (1939). “On the Self-Energy and the Electromagnetic Field of the Electron”. Physical Review 56: 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
[6] R. Oppenheimer (1930). “Note on the Theory of the Interaction of Field and Matter”. Physical Review 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
[7] W. E. Lamb; R. C. Retherford (1947). “Fine Structure of the Hydrogen Atom by a Microwave Method,”. Physical Review 72 (3): 241–243. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
[8] P. Kusch; H. M. Foley (1948). “On the Intrinsic Moment of the Electron”. Physical Review 73 (3): 412. Bibcode:1948PhRv...73..412F. doi:10.1103/PhysRev.73.412.
[9] Schweber, Silvan (1994). “Chapter 5”. QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. tr. 230. ISBN 978-0-691-03327-3.
[10] H. Bethe (1947). “The Electromagnetic Shift of Energy Levels”. Physical Review 72 (4): 339–341. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
[11] S. Tomonaga (1946). “On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields”. Progress of Theoretical Physics 1 (2): 27–42. doi:10.1143/PTP.1.27.
[12] J. Schwinger (1948). “On Quantum-Electrodynamics and the Magnetic Moment of the Electron”. Physical Review 73 (4): 416–417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
[13] J. Schwinger (1948). “Quantum Electrodynamics. I. A Covariant Formulation”. Physical Review 74 (10): 1439–1461. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
[14] R. P. Feynman (1949). “Space–Time Approach to Quantum Electrodynamics”. Physical Review 76 (6): 769–789. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
[15] R. P. Feynman (1949). “The Theory of Positrons”. Physical Review 76 (6): 749–759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
[16] R. P. Feynman (1950). “Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction”. Physical Review 80 (3): 440–457. Bibcode:1950PhRv...80..440F. doi:10.1103/PhysRev.80.440.
[17] a b F. Dyson (1949). “The Radiation Theories of Tomonaga, Schwinger, and Feynman”. Physical Review 75 (3): 486–502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
[18] F. Dyson (1949). “The S Matrix in Quantum Electrodynamics”. Physical Review 75 (11): 1736–1755. Bibcode:1949PhRv...75.1736D. doi:10.1103/PhysRev.75.1736.
[19] “The Nobel Prize in Physics 1965”. Nobel Foundation. Truy cập ngày 9 tháng 10 năm 2008.
[20] Feynman 1985, tr. 128
[21] G.S. Guralnik, C.R. Hagen, T.W.B. Kibble (1964). “Global Conservation Laws and Massless Particles”. Physical Review Letters 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
[22]G.S. Guralnik (2009). “The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles”. International Journal of Modern Physics A 24 (14): 2601–2627. arXiv:0907.3466. Bibcode:2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431.
Sách phổ thông
Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-12575-6.
Sách đại học
*De Broglie, Louis (1925). Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience.
*Feynman, Richard Phillips (1998). Quantum Electrodynamics. Westview Press; New Ed edition. ISBN 978-0-201-36075-2.
*Jauch, J.M.; Rohrlich, F. (1980). The Theory of Photons and Electrons. Springer-Verlag. ISBN 978-0-387-07295-1.
*Greiner, Walter; Bromley, D.A.,Müller, Berndt. (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
*Kane, Gordon, L. (1993). Modern Elementary Particle Physics. Westview Press. ISBN 978-0-201-62460-1.
*Miller, Arthur I. (1995). Early Quantum Electrodynamics : A Sourcebook. Cambridge University Press. ISBN 978-0-521-56891-3.
*Milonni, Peter W., (1994) The quantum vacuum - an introduction to quantum electrodynamics. Academic Press. ISBN 0-12-498080-5
*Schweber, Silvian, S. (1994). QED and the Men Who Made It. Princeton University Press. ISBN 978-0-691-03327-3.
*Schwinger, Julian (1958). Selected Papers on Quantum Electrodynamics. Dover Publications. ISBN 978-0-486-60444-2.
*Tannoudji-Cohen, Claude; Dupont-Roc, Jacques, and Grynberg, Gilbert (1997). Photons and Atoms: Introduction to Quantum Electrodynamics. Wiley-Interscience. ISBN 978-0-471-18433-1.
Tạp chí
*Dudley, J.M.; Kwan, A.M. (1996). “Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University”. *American Journal of Physics 64 (6): 694–698. Bibcode:1996AmJPh..64..694D. doi:10.1119/1.18234.
Liên kết ngoài
*Feynman's Nobel Prize lecture describing the evolution of QED and his role in it
*Feynman's New Zealand lectures on QED for non-physicists
*qed.wikina.org - Animations demonstrating QED
Nguồn : http://vi.wikipedia.org/wiki/ĐIỆN ĐỘNG LỰC HỌC LƯỢNG TỬ
Vài thông tin về Tái chuẩn hóa .
 |
| Nguồn : http://www.physics.ohio-state.edu/~ntg/srg/ |
Vào cuối những năm 1920, Dirac,Pauli,Weiskopff và Jordan xây dựng lí thuyết lượng tử cho tương tác giữa điện tử và photon ,mở rộng lí thuyết điện động lực trước đây của Maxwell. Lí thuyết điện động lực lượng tử sớm này đã rất thành công trong tính toán các quá trình tán xạ lượng tử khác nhau trong gần đúng bậc thấp nhất của lí thuyết nhiễu loạn. Đáng tiếc là tất cả những xây dựng này cho S-ma trận trong xấp xỉ bậc cao đều cho kết quả phân kì .
 |
Julian Schwinger
Born: 12 February 1918, New York, NY, USA Died: 16 July 1994, Los Angeles, CA, USA Affiliation at the time of the award: Harvard University, Cambridge, MA, USA Prize motivation: "for their fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles" Field: Quantum mechanics, quantum electrodynamics |
 |
Sin-Itiro Tomonaga
Born: 31 March 1906, Kyoto, Japan Died: 8 July 1979, Tokyo, Japan Affiliation at the time of the award: Tokyo University of Education, Tokyo, Japan Prize motivation: "for their fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles" Field: Quantum mechanics, quantum electrodynamics |
Đến cuối năm 1940,Tomonaga,Schwinger và Feynman tìm được cách xử lí vấn đề phân kì này bằng sự tái chuẩn hóa . Những nét cơ bản của tái chuẩn hoá là cộng thêm vào một thành phần chống lại sự phân kỳ ( counterterm ) trong phiếm hàm Hamilton của QED trước đây .Việc làm này đã đem lại kết quả phù hợp với 2 nguyên lí vật lí :
+Thứ nhất ,khối lượng điện tử trên lí thuyết phù hợp với khối lượng đo đạc.
+Thứ hai,tương tác giữa 2 điện tử trong khoảng cách lớn được quy về cổ điển .
Hai yêu cầu này đã dẫn đến 2 loại thành phần kháng phân kỳ về khối lượng và điện tích trong phiếm hàm Hamilton .
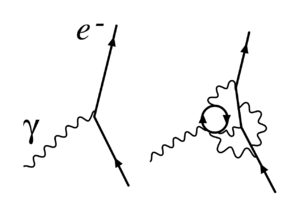 |
| Hình 1. Tái chuẩn hóa trong điện động lực học lượng tử: Sự tương tác đơn giản điện tử - photon xác định điện tích của điện tử tại một điểm tái chuẩn hóa được phát hiện bao gồm các tương tác phức tạp hơn tại một điểm khác . |
Như đã nói ở trên,những phần chống lại này tuy vô hạn , nhưng chúng lại loại bỏ được phần vô hạn của S-ma trận trong ký thuyết QED ban đầu . Sự loại trừ này vẫn để lại một vài thành phần thặng dư hữu hạn gọi là radiative corrections ( điều chỉnh bức xạ ). Những bước tính toán Tái chuẩn hóa của điều chỉnh bức xạ đối với các phần quá trình tán xạ (và năng lượng trạng thái cơ bản) sẽ cho kết quả trong mỗi bậc nhiễu loạn ,và những kết quả này phù hợp với thực nghiệm một cách đáng ngạc nhiên .
 |
| Hình 2. Một sơ đồ góp phần tán xạ electron-electron trong QED. Vòng lặp có sự phân kỳ cực tím. |
Hạn chế còn lại chủ yếu của lý thuyết Tái chuẩn hóa ( renormalized ) là phiếm hàm Hamilton QED với phần kháng phân kỳ là vô hạn . Mặc dù mọi thành phần vô hạn đều bị loại ra trong các công thức đối với các phần tử của S-ma trận nhưng chúng không hoàn toàn mất đi nếu ta muốn tính toán , chẳng hạn như sự tiến triển của vector hàm sóng và các quan sát . Sự thiếu hụt này có thể được điều chỉnh bởi một thủ thuật khác gọi là phép biến đổi thẳng hàng Unitar ( "unitary dressing transformation” ) được đề nghị đầu tiên trong O. W. Greenberg and S. S. Schweber, "Clothed particle operators in simple models of quantum field theory", Nuovo Cim. 8 (1958), 378 .
Trong lý thuyết sắp thẳng ( dressed ) ,cả phiếm hàm Hamiltonian và S-ma trận đều hữu hạn . Hơn nữa , những đặc trưng phi vật lý của Tái chuẩn hóa trong QED như " đám mây của các hạt ảo " bao quanh các điện tử và phân cực chân không sẽ không có mặt trong các nghiên cứu về các hạt được sắp thẳng ( "dressed particle " ) .
< In the end of 1920's Dirac, Pauli, Weiskopff, and Jordan formulated a quantum theory of interactions between electrons and photons in a loose analogy with Maxwell's classical electrodynamics. This early quantum electrodynamics (QED) was very successful in calculations of various scattering processes in lowest orders of the perturbation theory. Unfortunately, all contributions to the S-matrix in higher orders came out infinite.
In late 1940's Tomonaga, Schwinger and Feynman found the way to fix this problem of infinities by renormalization. The renormalization basically adds certain infinite counterterms to the Hamiltonian of the early QED. The form of these counterterms was selected such that the resulting theory satisfied two physical principles. First, the calculated electron's mass should be equal to the measured electron's mass. Second, the calculated interaction energy between two electrons at large distances should be equal to the classical expression . These two requirements lead to two types of renormalization counterterms in the Hamiltonian - the mass and charge renormalization counterterms.
As I said above, these counterterms are formally infinite, however, it appears that they exactly cancel the S-matrix infinities present in the original early QED. This cancelation leaves some residual finite terms called radiative corrections. Renormalized calculations of radiative corrections for scattering processes (and energies of bound states) yield finite results in each perturbation order, and these results agree with experiment to an astonishing precision.
The main remaining drawback of the renormalized theory is that the QED Hamiltonian with counterterms is infinite. Although, as I said, all infinities cancel out in formulas for S-matrix elements, they do not cancel out if you want to calculate, for example, the time evolution of state vectors and observables. This deficiency can be fixed by another trick called "unitary dressing transformation" first suggested in O. W. Greenberg and S. S. Schweber, "Clothed particle operators in simple models of quantum field theory", Nuovo Cim. 8 (1958), 378 .
In the "dressed" theory both the Hamiltonian and the S-matrix are finite. Moreover, such unphysical features of the renormalized QED as "clouds of virtual particles" surrounding electrons and "vacuum polarization" are absent in the "dressed particle" approach. >
Nguồn : Physics Forum .
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .





.jpg)
.jpg)


.jpg)
.jpg)
.jpg)

.jpg)
.jpg)





































