TÀI LIỆU TRỰC TUYẾN .

TÀI LIỆU TRỰC TUYẾN .

Trong các văn bản khoa học dưới đây có một số code cho phương trình vi phân , phương trình tích phân trong đó trình bày các phương pháp xấp xỉ như Runge-Kutta , Sokolov , tuyến tính hóa tương đương , phép biến đổi Laplace ... 
< Để đọc trực tuyến bạn Click chuột phải , chọn Open in a new tab > 

-------------------------------------------------------------------------------------------

Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.

Pure mathematics is, in its way, the poetry of logical ideas.

Albert Einstein .

Giới thiệu Blog TOÁN ĐƠN GIẢN .

Giới thiệu Blog TOÁN ĐƠN GIẢN

Các bạn có thể đọc các bài viết chuyên ngành Toán - Lý trên Blog TOÁN ĐƠN GIẢN ngay tại trang này bằng cách kéo thanh trượt ngang và dọc trên khung dưới đây .
Các bài viết về toán ứng dụng , các phần mềm minh hoạ và kỹ thuật sẽ được tác giả trình bày chi tiết trên
Blog TOÁN ĐƠN GIẢN . Rất mong nhận được những phản hồi ,đóng góp ý kiến  xây dựng của các bạn .

Trần hồng Cơ ,
26/05/2012

Alexa rank: 109 Daily pageviews: 24143266 Subscribe to http://cohtran.blogspot.com Xem bài viết trên Blog Toán - Cơ học ứng dụng http://cohtran.blogspot.com  Xem bài viết chuyên ngành trên Blog TOÁN ĐƠN GIẢN http://cohtran-toan-don-gian.blogspot.com/

 -------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
 Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .

TOÁN KỸ THUẬT - YOUTUBE

TOÁN KỸ THUẬT - YOUTUBE

More free eBooks?

***************************************************************

------------------------------------------------------------------------------------------------------------------

Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein .

THE RELAXATION FUNCTION PROBLEM .

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

The Relaxation function problem of an orthotropic cylinder .

Co. H. Tran. Faculty of Mathematics, University of Natural Sciences - VNU-HCMcoth123@math.com & cohtran@math.com
Copyright 2007
June 06 2007

NOTE:This worksheet demonstrates Maple's capabilities in researching the numerical and graphical solution of the relaxation function problem of an orthotropic cylinder .
All rights reserved. Copying or transmitting of this material without the permission of the authors is not allowed .

Use Maple 10


Abstract
The worksheet presents some thoughts about the plane strain problem of the viscous orthotropic composite materials cylinder under internal and external pressure with
respect to using the direct method . To compute the interior stress , from the elastic solution we use the correspondence principle and the inverse Laplace transform .

1. Analysis of the composite orthotropic cylinder :


We examine an orthotropic viscoelastic composite material cylinder which has the horizontal section within limit of 2 circles : r = a , r = b ( a <>

2. Direct method : The direct method is an approximate inversion technic based on the direct relation between the time dependence and the transformed solution . If the plot of the viscoelastic solution has small curvature when plotted with variables logt then : (1) where C is Euler's constant .. (1) is exact if , is proportional to logt . (1) can be rewritten : (2) Note that (2) is used when , has small curvature with respect to logt . From the correspondence principle we obtain the viscoelastic solution . (3) (4) (5) (6) The operator moduli : (7) We consider the relaxation test , in which , is a constant at t = 0 (8) . We have , , (9) By the similar way , we find out : (10) Assume that the relaxation moduli have power form : (11) where are constants . By applying the Laplace transfom for (11) , we obtain the operator moduli : (12) with the values of Gamma function : ; (13)

3. Parameters - The Numerical and Graphical Solution : >
restart;cycrstrecom:=proc(T,Gamma1,c1,P1,Q1,M1,d1) global P,Q,sigmaat1,sigmaat2,sigmabt2,sigmabt1,sigmaatisotropic,sigmabtisotropic ; local To,E,E1,M,d,j,Gamma,Gamma_form,gamma;with(inttrans):with(plottools):with(plots):print(" PARAMETERS DEFINITION : ");print( T=To,gamma=Gamma1,c=c1);;;print(" REPRESENTATION OF STRESS : ");;;;;print(" LAPLACE TRANSFORM OF MODULI : ");;;;;Gamma_form:=sqrt(E1[theta]/E1[r]);print(" EXPRESSION OF : ",gamma=Gamma_form;;print(" SUBSTITUTE ",c=c1 ,p =1/(2*t),gamma=Gamma) ;;;;print(" CHANGE THE PRESENTATION OF TIME INTO LOG(t/To) ");;;print(" OUTPUT DATA ");;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;M:=M1;;;d:=d1;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;printf(" s=log(t/To) sigma[Theta](a)(s)/P \n\n");
>
for j from 0 to M do printf("%10.1f %10.4f \n", -d*(10-j), subs(s=-d*(10-j),sigmaat2)) ; end do;
>
;;;;;;;;;;;;;;;;;;;;;;;;;;;;for j from 1 to M do printf("%10.1f %10.4f \n", d*j, subs(s=d*j,sigmaat2)) ; end do;
>
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;print(" NUMERICAL AND GRAPHICAL SOLUTION ");;printf("\n%s"," KET THUC BAI TOAN ONG TRU COMPOSITE DAN NHOT TRUC HUONG BANG PHUONG PHAP TRUC TIEP "); ;plot([sigmaat2,sigmaat2,sigmaatisotropic],s=-10..30,y=0.85..5.2,color=[grey,black,black],style=[line,point,point],thickness=1,symbol=[cross,diamond,cross],linestyle=1,axes=boxed,labels=["logt/To","sigma(a,t)/P"],legend=[`sigma(a,t)/P`,`sigma(a,t)/P`,`Isotropic solution`],title="Numerical solution");;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
>
end:>
cycrstrecom(1, .83, 1/2, 1, 0, 30, 1);


s=log(t/To) sigma[Theta](a)(s)/P -10.0 1.4286 -9.0 1.4286 -8.0 1.4287 -7.0 1.4289 -6.0 1.4294 -5.0 1.4305 -4.0 1.4335 -3.0 1.4409 -2.0 1.4595 -1.0 1.5056 0.0 1.6182 1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725 6.0 4.8419 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.0 2.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725 6.0 4.8419 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.0 2.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 21.0 1.8255 22.0 1.7910 23.0 1.7634 24.0 1.7413 25.0 1.7237 26.0 1.7096 27.0 1.6984 28.0 1.6894 29.0 1.6823 30.0 1.6766

KET THUC BAI TOAN ONG TRU COMPOSITE DAN NHOT TRUC HUONG BANG PHUONG PHAP TRUC TIEP

>

REFERENCES

[1] Ngo Thanh Phong , Nguyen Thoi Trung , Nguyen Dình Hien , Ap dung
phap gan dung bien doi Laplace nguoc de giai bai toan bien dang phang trong
lieu composite dan nhot truc huong , Tap chí phat trien KHCN , tap 7 , so 4 &
in Vietnamese ) , 2002 .

[2] R.A. Schapery , Stress Analysis of Viscoelastic Composite Materials ,
Edited by G.P.Sendeckyj ,Academic Press , Newyork –London , 1971 .


Legal Notice:
The copyright for this application is owned by the author(s). Neither Maplesoft nor the author are responsible for any errors contained within and are not liable for any damages resulting from the use of this material. This application is intended for non-commercial, non-profit use only. Contact the author for permission if you wish to use this application in for-profit activities.

View details online at the link : http://www.maplesoft.com/applications/app_center_view.aspx?AID=2136

The Relaxation function problem of an orthotropic cylinder .

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License. -------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein . 

BÀI TOÁN CHẢY CHẬM

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

BÀI TOÁN CHẢY CHẬM

Bài toán cụ thể - các tham số và lời giải :

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

The Solution Of A Variable Boundary Problem

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
 Pure mathematics is, in its way, the poetry of logical ideas. 

 Albert Einstein .

BÀI TOÁN CHÙNG ỨNG SUẤT

BÀI TOÁN  CHÙNG ỨNG SUẤT





This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

s=log(t/To) sigma[Theta](a)(s)/P

-10.0 1.4286
-9.0 1.4286
-8.0 1.4287
-7.0 1.4289
-6.0 1.4294
-5.0 1.4305
-4.0 1.4335
-3.0 1.4409
-2.0 1.4595
-1.0 1.5056 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.0 2.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725
0.0 1.6182 6.0 4.8419 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.02.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 21.0 1.8255 22.0 1.7910 23.0 1.7634 24.0 1.7413 25.0 1.7237 26.0 1.7096 27।0 1.6984 28.0 1.6894 29.0 1.6823 30.0 1.6766
1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725 6।0 4.8419

KET THUC BAI TOAN ONG TRU COMPOSITE DAN NHOT TRUC HUONG BANG PHUONG PHAP TRUC TIEP
Moi thac mac xin lien he :TRAN-HONG-CO .^^./ E-mail : cohtran@mail.com ^._.^ phone : ( 0 8 ) 54 2 5 0 8 7 4

The Relaxation function problem of an orthotropic cylinder .

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.


-------------------------------------------------------------------------------------------
 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

 Albert Einstein .

NHẬT KÝ KHOA HỌC

startBlog(25536168);
You must be logged in to post on this entry.Login New User SignupBack to NHAT KY
Sunday, May 20, 2007

Nhật ký ghi lại các hoạt động khoa học , nghiên cứu , trao đổi thông tin .
06:48 PM (UTC 8)Login New User SignupPost Comment Permalink


(comments 1-4)paramath: tac gia Tran Hong Co ða ðang toan bo luan van tren http://www.freewebs.com/paramath/tailieu gom 2 phan :
*p1 /. Luan van ða bao ve thanh cong tai Hoi ðong
*p2/. Luan van ( lan 1) hoan thanh thang 11 nam 2005 , sau ðo ðuoc bo sung vao p1/. Muc ðich cua cong viec nay la chong sao chep , tham khao neu khong co su cho phep cua chinh tac gia . June 10 , 2007 HCMC VIETNAM
June 10, 2007, 07:22 PM (UTC 8)paramath: ngày 10 tháng 6 , 2007 Frac-Mec ( Morozov)
June 10, 2007, 01:16 AM (UTC 8)

Solving the Viscous Composite Cylinder Problem by Sokolov's Method

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.



Solving the Viscous Composite Cylinder Problem by Sokolov's Method
Member Rating:
(rate this application)
Author:
Dr. Co Hong Tran
Application Type:
White Paper
Publish date:
**NEW** July, 2006
Related Products:
Maple 9.5
Language:
English
Options:

View as PDF (.pdf, 1,199.5kb)
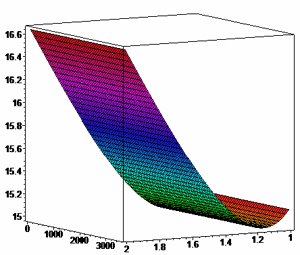
Abstract:The paper presents some thoughts about the plane strain problem of the viscous orthotropic composite materials cylinder under internal and external pressure with respect to using the average approximating method . To compute the interior stress , from the elastic solution we use the Volterra’s principle and Sokolov’s method in the corresponding integral equation to find the viscous solution


Thank you for your contact to the My Blog .

I have added my application and you can view it here:
http://www.maplesoft.com/applications/app_center_view.aspx?AID=1976

Please let me know if you have any questions or comments,

Solving The Viscous Composite Cylinder Problem By Sokolov’s Method

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

------------------------------------------------------------------------------------------

 LUẬN VỀ NHƯ KHÔNG 
 ( Cảm tác khi đọc bài CÁI KHÔNG TRONG LƯỢNG TỬ )



LÝ ĐẠO VÔ CÙNG NHƯ KHÔNG THỂ

DIỆT SINH tương hợp tại THIÊN DUYÊN

BẤT SINH BẤT DIỆT trùng lai HIỆP

ĐẠO LÝ giải MINH khó vẹn tuyền .


VÔ MINH KHÔNG THUYẾT gọi là DUYÊN ,

Điều TÂM BẤT ĐỊNH ẩn tại THIỀN

KHÔNG tri KHÔNG lý tâm THANH TỊNH

ĐẠO nơi ẨN NGHĨA ấy TỰ NHIÊN .


NGỘ như THỰC CHỨNG , TÂM VÔ PHÁP

ĐỊNH là VÔ ĐỊNH tự nhân DUYÊN

Ý quy VÔ Ý TÂM THIỀN ĐỊNH

LUẬN hay BẤT LUẬN chẳng tranh : PHIỀN .



 NGỘ ĐỊNH Ý LUẬN NHƯ THỰC CHỨNG
TÂM VÔ PHÁP ĐỊNH TỰ NHÂN DUYÊN
THIỀN QUY NHƯ Ý TÂM BẤT LUẬN
VÔ MINH DUYÊN KHỞI ẤY TẠI : THIỀN !


Bạn muốn gặp Ta ? Ta gặp Bạn ?
KHÔNG đời KHÔNG Đạo chẳng lụy PHIỀN
TÁI SINH nhất kiếp NHƯ LAI kiếp
Tách trà nhạt khói thoảng AN NHIÊN .




Tri âm Bạn hữu vui thiên tuế

Nhật nguyệt đôi vầng sáng GIÁC VIÊN

Ngộ Định Ý Luận Như Không Pháp .

Nhất Dạ miên trường Tái Sinh Duyên .











Trần hồng Cơ

Ngộ Định Ý Luận Như Không Pháp .

Nhất Dạ miên trường Tái Sinh Duyên .

Bản gốc :  09/01/2006




This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

 -------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
 Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein . 

THE AVERAGE APPROXIMATING METHOD ON FUNCTIONAL ADJUSTMENT QUANTITY

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

THE AVERAGE APPROXIMATING METHOD ON FUNCTIONAL ADJUSTMENT QUANTITY FOR SOLVING

 Volterra Integral Equation of the second kind . 

( corrected for solving integral equations with Hereditary kernels )

by Co.H Tran , University of Natural Sciences , HCMC Vietnam -

Institute of Applied Mechanics , HCMC - coth123@math.com & coth123@yahoo.com

Copyright 2004

Sat , November 06 2004

----------------------------------------------------------------------------------------------------

** Abstract : Solving the Volterra's integral equation II with applying the Neumann series and the average approximating method on functional adjustment quantity .

** Subjects: Viscoelasticity Mechanics , The Integral equation .

-----------------------------------------------------------------------------------------------------

Copyright
Co.H Tran --
. The Average Approximating Method on Functional Adjustment Quantity ( Sokolov's method ) All rights reserved. No copying or transmitting of this material is allowed without the prior written permission of Co.H Tran

The Average Approximating Method on Functional Adjustment Quantity ( Sokolov's method )

In consideration of The Volterra Integral Equation II ( second kind ) , we find the explicit expression for the resolvent kernel ( t , t ) in the general form : v = ( 1 + K* ) u here : arbitrary parameter . The solution of u can be represented with the Neumann series : . The resolvent operator * is determined by a Neumann series : , then the kernel . The convergence of this series must be investigated in a connection with the Neumann series . The average approximating method on the functional adjustment quantity ( Sokolov's method ) makes increasing for the rate of convergence of this series . From the first approximation of the solution u , we find the adjustment quantity for the next and so on . We consider the following equation : ( 1 ) the first approximation : ( 2 ) by choosing the initial adjustment quantity : ( 3 ) From ( 2 ) and ( 3 ) we obtain : ( 4 ) with ( 5 ) the n-th approximation : ( 6 ) and the adjustment quantity of the n-th order can then be written as : ( 7 ) here ( 8 ) . From ( 6 ) , ( 7 ) and ( 8 ) we have : ( 9 ) Denoting the formulas ( 6 ) to ( 9 ) can be carried out by the computer programming language. We can show that the convergence condition of this method is ( 10 ) here : the project-operator from the Banach's space B into its space Bo ( the solution u B )
Sokolov's method
As seen , the first approximation : We choose the initial adjustment quantity : with ;
adjustment quantity of the order i-th can be expresssed :
The coefficient
Compare with the initial function and we have the error estimated :

It is easy to see that (x) n is a Cauchy sequence in L2(T) as k -> . It follows from the completeness of L2(T) that it converges in the L2 sense to a sum g in L2(T). That is, we have lim (x) -(x) = 0 k ->

Legal Notice: The copyright for this application is owned by Maplesoft. The application is intended to demonstrate the use of Maple to solve a particular problem. It has been made available for product evaluation purposes only and may not be used in any other context without the express permission of Maplesoft.

I have added my application and you can view it here: : http://www.maplesoft.com/applications/app_center_view.aspx?AID=1952

The Average Approximating Method On Functional Adjustment Quantity For Solving The Volterra Integral Equation II

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

Please let me know if you have any questions or commen

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.


-------------------------------------------------------------------------------------------

 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein .