BÀI TOÁN CHÙNG ỨNG SUẤT

BÀI TOÁN  CHÙNG ỨNG SUẤT





This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

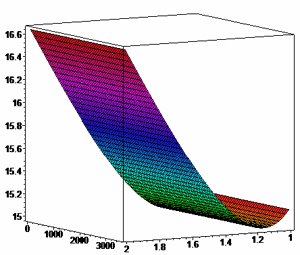
s=log(t/To) sigma[Theta](a)(s)/P

-10.0 1.4286
-9.0 1.4286
-8.0 1.4287
-7.0 1.4289
-6.0 1.4294
-5.0 1.4305
-4.0 1.4335
-3.0 1.4409
-2.0 1.4595
-1.0 1.5056 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.0 2.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725
0.0 1.6182 6.0 4.8419 7.0 4.5127 8.0 4.1110 9.0 3.7260 10.0 3.3828 11.0 3.0857 12.0 2.8323 13.02.6184 14.0 2.4396 15.0 2.2913 16.0 2.1691 17.0 2.0691 18.0 1.9877 19.0 1.9217 20.0 1.8684 21.0 1.8255 22.0 1.7910 23.0 1.7634 24.0 1.7413 25.0 1.7237 26.0 1.7096 27।0 1.6984 28.0 1.6894 29.0 1.6823 30.0 1.6766
1.0 1.8804 2.0 2.4264 3.0 3.3300 4.0 4.3240 5.0 4.8725 6।0 4.8419

KET THUC BAI TOAN ONG TRU COMPOSITE DAN NHOT TRUC HUONG BANG PHUONG PHAP TRUC TIEP
Moi thac mac xin lien he :TRAN-HONG-CO .^^./ E-mail : cohtran@mail.com ^._.^ phone : ( 0 8 ) 54 2 5 0 8 7 4

The Relaxation function problem of an orthotropic cylinder .

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.


-------------------------------------------------------------------------------------------
 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

 Albert Einstein .

NHẬT KÝ KHOA HỌC

startBlog(25536168);
You must be logged in to post on this entry.Login New User SignupBack to NHAT KY
Sunday, May 20, 2007

Nhật ký ghi lại các hoạt động khoa học , nghiên cứu , trao đổi thông tin .
06:48 PM (UTC 8)Login New User SignupPost Comment Permalink


(comments 1-4)paramath: tac gia Tran Hong Co ða ðang toan bo luan van tren http://www.freewebs.com/paramath/tailieu gom 2 phan :
*p1 /. Luan van ða bao ve thanh cong tai Hoi ðong
*p2/. Luan van ( lan 1) hoan thanh thang 11 nam 2005 , sau ðo ðuoc bo sung vao p1/. Muc ðich cua cong viec nay la chong sao chep , tham khao neu khong co su cho phep cua chinh tac gia . June 10 , 2007 HCMC VIETNAM
June 10, 2007, 07:22 PM (UTC 8)paramath: ngày 10 tháng 6 , 2007 Frac-Mec ( Morozov)
June 10, 2007, 01:16 AM (UTC 8)

Solving the Viscous Composite Cylinder Problem by Sokolov's Method

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.



Solving the Viscous Composite Cylinder Problem by Sokolov's Method
Member Rating:
(rate this application)
Author:
Dr. Co Hong Tran
Application Type:
White Paper
Publish date:
**NEW** July, 2006
Related Products:
Maple 9.5
Language:
English
Options:

View as PDF (.pdf, 1,199.5kb)
Abstract:The paper presents some thoughts about the plane strain problem of the viscous orthotropic composite materials cylinder under internal and external pressure with respect to using the average approximating method . To compute the interior stress , from the elastic solution we use the Volterra’s principle and Sokolov’s method in the corresponding integral equation to find the viscous solution


Thank you for your contact to the My Blog .

I have added my application and you can view it here:
http://www.maplesoft.com/applications/app_center_view.aspx?AID=1976

Please let me know if you have any questions or comments,

Solving The Viscous Composite Cylinder Problem By Sokolov’s Method

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

------------------------------------------------------------------------------------------

 LUẬN VỀ NHƯ KHÔNG 
 ( Cảm tác khi đọc bài CÁI KHÔNG TRONG LƯỢNG TỬ )



LÝ ĐẠO VÔ CÙNG NHƯ KHÔNG THỂ

DIỆT SINH tương hợp tại THIÊN DUYÊN

BẤT SINH BẤT DIỆT trùng lai HIỆP

ĐẠO LÝ giải MINH khó vẹn tuyền .


VÔ MINH KHÔNG THUYẾT gọi là DUYÊN ,

Điều TÂM BẤT ĐỊNH ẩn tại THIỀN

KHÔNG tri KHÔNG lý tâm THANH TỊNH

ĐẠO nơi ẨN NGHĨA ấy TỰ NHIÊN .


NGỘ như THỰC CHỨNG , TÂM VÔ PHÁP

ĐỊNH là VÔ ĐỊNH tự nhân DUYÊN

Ý quy VÔ Ý TÂM THIỀN ĐỊNH

LUẬN hay BẤT LUẬN chẳng tranh : PHIỀN .



 NGỘ ĐỊNH Ý LUẬN NHƯ THỰC CHỨNG
TÂM VÔ PHÁP ĐỊNH TỰ NHÂN DUYÊN
THIỀN QUY NHƯ Ý TÂM BẤT LUẬN
VÔ MINH DUYÊN KHỞI ẤY TẠI : THIỀN !


Bạn muốn gặp Ta ? Ta gặp Bạn ?
KHÔNG đời KHÔNG Đạo chẳng lụy PHIỀN
TÁI SINH nhất kiếp NHƯ LAI kiếp
Tách trà nhạt khói thoảng AN NHIÊN .




Tri âm Bạn hữu vui thiên tuế

Nhật nguyệt đôi vầng sáng GIÁC VIÊN

Ngộ Định Ý Luận Như Không Pháp .

Nhất Dạ miên trường Tái Sinh Duyên .











Trần hồng Cơ

Ngộ Định Ý Luận Như Không Pháp .

Nhất Dạ miên trường Tái Sinh Duyên .

Bản gốc :  09/01/2006




This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

 -------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
 Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein . 

THE AVERAGE APPROXIMATING METHOD ON FUNCTIONAL ADJUSTMENT QUANTITY

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

THE AVERAGE APPROXIMATING METHOD ON FUNCTIONAL ADJUSTMENT QUANTITY FOR SOLVING

 Volterra Integral Equation of the second kind . 

( corrected for solving integral equations with Hereditary kernels )

by Co.H Tran , University of Natural Sciences , HCMC Vietnam -

Institute of Applied Mechanics , HCMC - coth123@math.com & coth123@yahoo.com

Copyright 2004

Sat , November 06 2004

----------------------------------------------------------------------------------------------------

** Abstract : Solving the Volterra's integral equation II with applying the Neumann series and the average approximating method on functional adjustment quantity .

** Subjects: Viscoelasticity Mechanics , The Integral equation .

-----------------------------------------------------------------------------------------------------

Copyright
Co.H Tran --
. The Average Approximating Method on Functional Adjustment Quantity ( Sokolov's method ) All rights reserved. No copying or transmitting of this material is allowed without the prior written permission of Co.H Tran

The Average Approximating Method on Functional Adjustment Quantity ( Sokolov's method )

In consideration of The Volterra Integral Equation II ( second kind ) , we find the explicit expression for the resolvent kernel ( t , t ) in the general form : v = ( 1 + K* ) u here : arbitrary parameter . The solution of u can be represented with the Neumann series : . The resolvent operator * is determined by a Neumann series : , then the kernel . The convergence of this series must be investigated in a connection with the Neumann series . The average approximating method on the functional adjustment quantity ( Sokolov's method ) makes increasing for the rate of convergence of this series . From the first approximation of the solution u , we find the adjustment quantity for the next and so on . We consider the following equation : ( 1 ) the first approximation : ( 2 ) by choosing the initial adjustment quantity : ( 3 ) From ( 2 ) and ( 3 ) we obtain : ( 4 ) with ( 5 ) the n-th approximation : ( 6 ) and the adjustment quantity of the n-th order can then be written as : ( 7 ) here ( 8 ) . From ( 6 ) , ( 7 ) and ( 8 ) we have : ( 9 ) Denoting the formulas ( 6 ) to ( 9 ) can be carried out by the computer programming language. We can show that the convergence condition of this method is ( 10 ) here : the project-operator from the Banach's space B into its space Bo ( the solution u B )
Sokolov's method
As seen , the first approximation : We choose the initial adjustment quantity : with ;
adjustment quantity of the order i-th can be expresssed :
The coefficient
Compare with the initial function and we have the error estimated :

It is easy to see that (x) n is a Cauchy sequence in L2(T) as k -> . It follows from the completeness of L2(T) that it converges in the L2 sense to a sum g in L2(T). That is, we have lim (x) -(x) = 0 k ->

Legal Notice: The copyright for this application is owned by Maplesoft. The application is intended to demonstrate the use of Maple to solve a particular problem. It has been made available for product evaluation purposes only and may not be used in any other context without the express permission of Maplesoft.

I have added my application and you can view it here: : http://www.maplesoft.com/applications/app_center_view.aspx?AID=1952

The Average Approximating Method On Functional Adjustment Quantity For Solving The Volterra Integral Equation II

Publish at Calameo or read more publications
Author : Co Hong Tran MMPC-VN.

Please let me know if you have any questions or commen

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.


-------------------------------------------------------------------------------------------

 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
Pure mathematics is, in its way, the poetry of logical ideas. 

Albert Einstein .