KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D -
Phần 7 . Pe - Sp (43-53)
Lời nói đầu .
Như chúng ta đã biết loạt bài " DANH MỤC CÁC ĐƯỜNG CONG " được trình bày trước đây gồm có 3 phần . Nội dung của những phần này là liệt kê các phương trình , tên gọi cùng các giai thoại và chú thích lịch sử của một số đường cong thường xuất hiện trong toán học , vật lý , thiên văn và nhiều ngành kỹ thuật khác .
Bạn đọc có thể theo dõi chi tiết trên các trang sau :
Phần 3 .
http://cohtran.blogspot.com/2012/09/danh-muc-cac-duong-cong-3.
Phiên bản mới nhất đăng trên
http://tusach.thuvienkhoahoc.com/wiki/Danh_mục_và_lịch_sử_các_đường_cong
Tiếp theo sau đây là chuyên mục " KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D " ,
Mục đích của chuỗi bài viết này là khảo sát đồ thị các đường cong bằng các công cụ trực tuyến (online) hoặc trình ứng dụng ( phần mềm offline ) .
Việc thực hành này là hết sức cần thiết và cũng mang lại nhiều kết quả lợi ích . Một mặt nó giúp chúng ta hiểu rõ hơn về các tính chất đặc trưng của các đường cong , mặt khác cũng là dịp làm quen với một số trình ứng dụng có quy mô lớn và tốc độ xử lý rất mạnh . Từ đó chúng ta có thêm kiến thức về đồ họa phục vụ cho việc nghiên cứu hoặc giải quyết những bài toán cụ thể trong phạm vi chuyên môn của mình .
Xin trân trọng giới thiệu cùng bạn đọc .
Trần hồng Cơ
Ngày 23 / 06 / 2014
-----------------------------------------------------------------------------------------------------------
Chào các bạn , trong phần 6 chúng ta đã khảo sát và thực hành đồ họa các đường cong từ Ka đến Pa ( 33 - 42 ) bằng các trình ứng dụng ( GP , GX và Maple V ) và công cụ trực tuyến ( FooPlot , DESMOS , Flashandmath ) . Bạn đọc cũng đã làm quen một số lệnh và tùy chọn đồ họa 3D cho trình ứng dụng Maple V trong mục II của bài viết . Nội dung phần 6 này sẽ được tiếp tục với các khái niệm xây dựng đường cong , sử dụng các trình ứng dụng và các công cụ trực tuyến vẽ đồ thị và tìm hiểu các lệnh đồ họa 3D của Maple V , các procedure tiện ích cho tính toán độ cong , chiều dài cung .. .
Giống như phần trước , ở cuối mỗi tiểu mục là phần lưu trữ những tài liệu ( dạng pdf , nb , ggb ,gsp ) , hình ảnh minh họa (jpg , png , gif ) và những tập tin multimedia (mov , flv ,swf ... ) về các đường cong để bạn đọc tiện tham khảo .
I. Vẽ đồ thị các đường cong từ Pe - Sp [43-53] bằng trình ứng dụng và công cụ trực tuyến .
1.1 Pearls of de Sluze (Đường viền Sluze) [43]
A . Khái niệm .
Họ các đường cong $y^n = k.(a-x)^p.x^m$ với các số mũ n , p , m nguyên dương , a và b là hai số thực khác 0 , được gọi là " đường viền Sluze ". René de Sluze , nhà toán học xứ Flemish (thuộc Bỉ) đã nghiên cứu những đường cong này và bài toán thể tích tròn xoay giới hạn bởi cissoid quanh tiệm cận của nó trong tác phẩm Miscellanie. Vài hình dạng đặc biệt của đường viền Sluze như sau ( xem hình )
+Nếu $ n = 4, p = 3, m = 2, a = k = 1$ , ta có $ y^4 = x^2 (1 - x)^3 $ .
Khi đó điều kiện của x sẽ là $ x \leq 1$ , khai căn bậc 4 cho hai vế phương trình trên thu được
$y=\pm \sqrt{|x|}(1-x)^{3/4}$ Đồ thị có dạng
Đạo hàm của hàm số : $y'=\frac{2-5x}{4\sqrt{x}(1-x)^{1/4}}$ , các giá trị của đạo hàm tại $x = 0$ và $x=1$ là $ \infty $ nên tiếp tuyến với đường cong tại $x=0 , y = 0$ và $x=1,y = 0$ song song với trục tung .
+Nếu $n = 4, p = 2, m = 5, a = k = 1$ ta có $y^4 = x^2 (1 - x)^5$
hay $y= \pm \sqrt{|x|}(1-x)^{5/4}$ , điều kiện $ x \leq 1$ . Đồ thị có dạng
Đạo hàm của hàm số : $ y' = \frac{(2-7x)(1-x)^{1/4}}{4\sqrt{x}}$ , giá trị đạo hàm tại $x=0$ là $ \infty$ nên tiếp tuyến tại $x=0 , y =0$ song song với trục tung .
Giá trị của đạo hàm tại $x = 1$ bằng 0 nên tiếp tuyến tại $x =1, y =0$ song song với trục hoành .
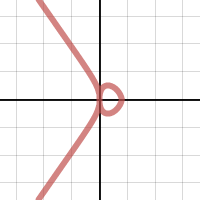
+Nếu $n = 4, p = 4 , m = 2 , a = k = 1$ phương trình có dạng $ y^4 = x^2 (1 - x)^4$
hay $y=\pm |1-x|. \sqrt{|x|}$ . Đồ thị hàm số như sau
+Nếu $n = 5 , m = 3 , p = 4, a = k = 1$ ta có $y^5 = x^3(1 - x)^4 $ . Đồ thị hàm số có dạng
+Nếu $n = 4 , m = 5 , p = 3, a = k = 1$ ta có $y^4 = x^5(1 - x)^3$ . Đồ thị hàm số như sau
Trong trường hợp này đường viền Sluze khép kín .
+Chiều dài cung và chu vi
Xem trực tuyến
http://goo.gl/jKkHWE
+Diện tích giới hạn được tính bởi
xem trực tuyến
http://goo.gl/i8Z8ed
+Chiều dài cung
+Độ cong
+Chu vi
+Diện tích
Xem hình động :
https://www.desmos.com/calculator/bu2fsptcqr
Các đường liên hợp
Xem
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y^n = k(a-x)^p.x^m$
y^n = k*(a-x)^p*x^m
Nhập liệu bằng DESMOS chọn các giá trị cho thanh trượt
1.2 Pear-Shaped Quartic (Đường bậc 4 hình lê) [44]
A . Khái niệm .
- G. de Longchamps , nhà toán học Pháp đã nghiên cứu về đường bậc 4 hình lê vào năm 1886. Phương trình biểu diễn có dạng : $b^2y^2 = x^3.(a-x)$ ( xem hình ) .
-Đường bậc 4 hình lê được xây dựng như sau
Xét đường tròn (C) có đường kính $OA , A(a,0)$ , đường thẳng $x = b , b : const$ . Điểm P di động trên (C) , dựng PQ _|_ $x = b $ tại Q . Từ P dựng đường thẳng vuông góc với PQ , cắt OQ tại M . Quỹ tích của M chính là đường bậc 4 hình lê (xem hình sau ) .
+Chiều dài cung $L[\alpha,\beta]$ =
Ví dụ với $a =1 , b = 2 , \alpha = 0 , \beta =4$ ta có $L[0,1]$ =
Xem WA trực tuyến
http://goo.gl/NcMHb8
Các bạn có thể dùng MapleV tính toán gần đúng cho tích phân bằng công thức Simpson như sau
Vì $\beta =1$ hàm Lx không xác định để áp dụng được công thức Simpson ta chọn $\beta =0.98546$ thu được kết quả tương tự như WA .
+Độ cong $K(x)=\frac{2b^2(8x^2-12ax+3a^2)}{[x(3a-4x)^2+4b^2(a-x)]^\frac{3}{2}.\sqrt{x}}$
Dùng MapleV tìm độ cong
+Chu vi
Giá trị gần đúng khi $a =1 , b = 2 , \alpha = 0 , \beta =4$ ta có $P = 2 L[0,1]$ =
+Diện tích $S = \frac{\pi a^3}{8b}$
Từ phương trình $b^2y^2 = x^3.(a-x)$ ta có $y= \pm \frac{x \sqrt{a-x}}{b}$
Diện tích giới hạn bởi một nhánh đường cong và trục hoành là
$S_{(C),Ox}= \int_{0}^{a}\frac{x \sqrt{a-x}}{b}dx$
-Một dạng khác của đường cong bậc 4 này có tên là piriform _ còn gọi là đường con quay (peg top) _ có phương trình trong hệ tọa độ Descartes là
$a^4y^2=b^2x^3(2a-x)$
và phương trình tham số
$x=a(1+sint) ; y=bcost(1=sint)$ với $t \in [0,2 \pi]$
+Diện tích của piriform là $S = πab$
+Độ cong (curvature) của piriform là
$K(t)= \frac{ab[2+3\sin t + \sin3t]} {2(a^2 \cos^2 t +b^2[\cos2t - \sin t]^2)^{3/2}}$
( theo
http://mathworld.wolfram.com/PiriformCurve.html ) .
Xem tài liệu về piriform trên
slideshare
Các đường liên hợp
Xem
http://youtu.be/KWs_XYOzZXQ
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
b^2*y^2 = x^3*(a-x)
Nhập liệu bằng DESMOS , chọn giá trị cho thanh trượt a , b
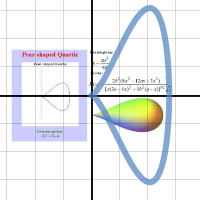
Xem hình động :
https://www.desmos.com/calculator/rdtmaq88qr
1.3 Plateau Curves (Đường cong Plateau) [45]
A . Khái niệm .
-Trong hình học , đường hình quạt (sectrix) Maclaurin được định nghĩa là quỹ tích giao điểm của hai đường thẳng quay cùng một chiều với tốc độ không đổi từ 2 điểm phân biệt được gọi là 2 cực . Tương tự, đường hình quạt Maclaurin cũng có thể được định nghĩa là một đường cong có phương trình trong hệ tọa độ lưỡng giác (biangular) là tuyến tính. Tên gọi này có nguồn gốc từ đường trisectrix của Maclaurin , thuộc họ đường cong sectrix , có nghĩa là chúng có thể được sử dụng để chia một góc thành một số lượng nhất định thành những phần bằng nhau . Những trường hợp đặc biệt khác của họ đường cong này còn được gọi là arachnida hoặc araneidans vì có hình dạng giống như nhện , và đường cong Plateau ( xem hình sau ) .
 |
| Sectrix of Maclaurin: với q0=PI/2 và K=3 |
-Xét hai đường thẳng $d , d_{1}$ quay cùng chiều từ hai cực $P(0,0)$và $P_{1}(2a,0)$ .
Tại thời điểm s đường thẳng $d$ tại cực $P(0,0)$ và $d_{1}$ tại cực $P_{1}(2a,0)$ có góc quay tương ứng là $θ =ks+ \alpha $ và $θ_{1} =k_{1}s+ \alpha_{1} $ , trong đó $k,k_{1}, \alpha , \alpha_{1}$ là các hằng số .
Khử tham số s từ các góc quay ta có $θ_{1} =qθ+h$ với $q=k_{1}/k$ và $h=\alpha_{1}- q \alpha$
Gọi M là giao điểm của 2 đường thẳng và $\beta = \angle [ d,d_{1}]$ khi đó $\beta =θ_{1} - θ $ .
Đặt $r = PM$ theo định lý hàm sin trong $\bigtriangleup PMP_{1}$ ta có
$\frac{r}{sinθ_{1}}= \frac{2a}{sin \beta}$
Vậy $r = 2a. \frac{sinθ_{1}}{sin \beta} = 2a. \frac{sin(qθ+h)}{sin(qθ+h - θ )}$
Hay $r =2a. \frac{sin(qθ+h)}{sin[(q-1)θ+h ]}$ .
Đây chính là phương trình đường hình quạt Maclaurin trong hệ tọa độ cực (xem hình sau ) .
-Khi $h=0,q=n ; n \in N , n > 2 $ ta có đường hình nhện arachnida hoặc araneidan loại 1 :
$r =2a. \frac{sin(nθ)}{sin[(n-1)θ]}$
-Khi $h=0,q= -n ; n \in N , n > 1 $ ta có đường hình nhện arachnida hoặc araneidan loại 2 :
$r =-2a. \frac{sin(nθ)}{sin[(n+1)θ]}$
-Khi $h=0 , q \in Q $ ta có đường cong Plateau :
$r =2a. \frac{sin(qθ)}{sin[(q-1)θ]}$
-Tham số hóa đường cong bằng cách đặt $q=m/n ; m , n \in Z$ và $θ=nt$ với t là tham số , ta có
$x=a. \frac{sin[(m+n)t+h]}{sin[(m-n)t+h]}$
$y=2a. \frac{sin(mt+h)sin(nt)}{sin[(m-n)t+h]}$
Khi $h=0$ ta có phương trình tham số của đường cong trong hệ tọa độ Descartes là
$x=a. \frac{sin[(m+n)t]}{sin[(m-n)t]}$
$y=2a. \frac{sin(mt)sin(nt)}{sin[(m-n)t]}$
-Một số hình dạng của đường cong Plateau
( nhập liệu với phương trình $r =2a. \frac{sin(qθ)}{sin[(q-1)θ]}$ trong hệ tọa độ cực )
+Chiều dài cung
+Độ cong .
Công thức tính độ cong khá phức tạp , tùy thuộc vào các tham số là a , q và θ .
Dưới đây là một procedure tác giả viết bằng MapleV có tên là
docongplateau - dùng để tính độ cong C(t) , về chi tiết sẽ được trình bày ở phần II của bài viết này .
Ví dụ với $a =1,q=4/3, t= \pi /2$ ta có :
+Chu vi
+Diện tích
Các đường liên hợp
Xem
http://youtu.be/SJSEHbdFeb8
B. Phương trình .
Phương trình tham số trong hệ tọa độ Descartes:
$x=a. \frac{sin[(m+n)t]}{sin[(m-n)t]}$
$y=2a. \frac{sin(mt)sin(nt)}{sin[(m-n)t]}$
x = a*sin((m+n)*t)/sin((m-n)*t)
y = 2*a*sin(m*t)*sin(n*t)/sin((m-n)*t)
Phương trình đường cong trong hệ tọa độ cực:
$r =2a. \frac{sin(qθ)}{sin[(q-1)θ]}$
Nhập liệu bằng DESMOS chọn các giá trị cho thanh trượt a , q .
r = 2*a*sin(q*t)/sin((q-1)*t)
Thực hành với
a =1 , q = 1.5 ( đường Limacon )
a =1 , q = 2 ( đường tròn tâm $I(2,0)$ bán kính $R= 2a = 2$ )
a =1.5 , q = 2 ( đường tròn tâm $I(2,0)$ bán kính $R = 2a = 2 \times 1.5 = 3$ )
a từ -2 đến 2 , q = 1.3 .
a từ - 2 đến 2 , q = 3 .

Xem trực tuyến
https://www.desmos.com/calculator/zsryeroiep
1.4 Pursuit Curve (Đường cong đuổi – Bouguer) [46]
A . Khái niệm .
Bài toán dẫn xuất của đường cong đuổi - Bouguer như sau
Xét điểm T (Thỏ) di chuyển dọc theo một đường cong cho trước, điểm C (Cáo) luôn hướng về phía T và hai điểm T và C cùng di chuyển với vận tốc đều thỏa mãn 2 tính chất sau :
1. Điểm C luôn hướng về điểm T .
2. Vận tốc điểm C tỷ lệ với vận tốc điểm T .
Khi đó quỹ tích điểm C được mô tả là một đường cong đuổi .
Nhà khoa học Pháp Pierre Bouguer đã xem xét hệ chuyển động trên trong trường hợp tổng quát năm 1732.
Trường hợp đặc biệt, khi T di động trên một đường thẳng cũng đã được Pierre Bouguer nghiên cứu chi tiết sau này .
( xem hình )
-Tọa độ của điểm C và T được xác định bởi các hàm vector
$\vec{C}=(x(t),y(t))$ và $\vec{T}=(0,y(t)=rt)$
Điều kiện đầu của hàm vector $\vec{C}=(x(t),y(t))$ là $\vec{C}(0)=(x(0),y(0))=(a,0)$
Từ tính chất 2 , ta có $||\vec{C'}||=k.||\vec{T'}||$
Quãng đường C đi được là $ s=||\vec{C}'||t=k||\vec{T}'||=k||(0,(rt)')||=krt$
Khi đó $\frac{ds}{dt}=kr$
Từ tính chất 1 , ta có $\frac{\vec{C'}}{||\vec{C'}||}=\frac{\vec{T}-\vec{C}}{||\vec{T}-\vec{C}||}$
hay $\vec{C'}=||\vec{C'}||.\frac{\vec{T}-\vec{C}}{||\vec{T}-\vec{C}||}$ (1)
Từ tính chất 2 , ta có $||\vec{C'}||=k.||\vec{T'}||$ , thay vào (1) ta thu được
$\vec{C'}=k.||\vec{T'}||.\frac{\vec{T}-\vec{C}}{||\vec{T}-\vec{C}||}$
Dưới dạng vector
$(x',y')=k||(0,(rt)')||\frac{(0,rt)-(x,y)}{||(0,rt)-(x,y)||}$
$=kr\frac{(-x,rt-y)}{\sqrt{r^2+(rt-y)^2}}$
Hay dưới dạng hệ thống phương trình vi phân
$x'=-kr.\frac{x}{r^2+(rt-y)^2}$ (2)
$y'=kr.\frac{rt-y}{r^2+(rt-y)^2}$ (3)
Lấy (3) chia (2) ta sẽ có
$\frac{y'}{x'}=\frac{y-rt}{x}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{dy}{dx}$
$\Leftrightarrow x \frac{dy}{dx}=y-rt$
Vi phân hai vế theo x : $\frac{dy}{dx}+x \frac{d^2y}{dx^2}=\frac{dy}{dx}-r \frac{dt}{dx}$
dẫn đến $x \frac{d^2y}{dx^2}=-r \frac{dt}{dx}$ (4)
Để ý rằng $\frac{dt}{dx}=\frac{dt}{ds}.\frac{ds}{dx}=-\frac{dt}{ds}.\sqrt{1+ \left ( \frac{dy}{dx} \right )^2 }=-\frac{1}{kr}.\sqrt{1+ \left ( \frac{dy}{dx} \right )^2 }$
Thế vào (4) :
$x\frac{d^2y}{dx^2}=\sqrt{1+ \left ( \frac{dy}{dx} \right )^2 }$ (5)
Đặt $p=\frac{dy}{dx}\Rightarrow x \frac{dp}{dx}=\sqrt{1+ p^2 }$
Dùng phương pháp tách biến giải phương trình vi phân trên ta có :
hay $p=\frac{dy}{dx}=\frac{1}{2}\left ( (x/a)^{1/k}-(a/x)^{1/k} \right )$
Tích phân phương trình này , thu được nghiệm $y(x)$
- Bạn đọc có thể giải phương trình vi phân (5) và vẽ đồ thị nghiệm $y(x)$ bằng trình ứng dụng MapleV như sau
Hoặc sử dụng công cụ trực tuyến WA với nhập liệu là : x*diff(diff(y,x),x)=sqrt(1+(diff(y,x))^2)
Xem :
http://goo.gl/i939eE
Khi đó phương trình đường cong trong hệ tọa độ Descartes có dạng tổng quát là
$y = Ax^2 - Bln(x)$
Hay $y = cx^2 - ln(x)$
Bài toán về đường cong đuồi Bouguer có rất nhiều ứng dụng trong vật lý ,đặc biệt là lĩnh vực quốc phòng khi nghiên cứu về kỹ thuật tên lửa tìm diệt , hoặc tên lửa phá hủy vệ tinh .
Các mô hình về đường cong đuổi tam giác , tứ giác , ngũ giác và lục giác được biểu diễn như sau đây
Các mô hình về đường cong đuổi cổ điển và song song
+chiều dài cung
Công thức tính chiều dài cung cho đường cong đuổi Bouguer khá phức tạp , tùy thuộc vào các tham số là c , a và b . Sử dụng công cụ trực tuyến WA để tính chiều dài cung .
Truy cập WA theo link
http://www.wolframalpha.com/input/
Các bạn nhập liệu bằng lệnh int(sqrt((2cx-1/x)^2+1))
Xem :
http://goo.gl/N65ixp
Sau đó thay các tham số c , a , b bằng số liệu cho trước .
Ví dụ với $c =1,a =1, b= 2$ ta có :
Xem trực tuyến :
http://goo.gl/5JNNr0
Dưới đây là một procedure tác giả viết bằng MapleV có tên là
cdcungbouguer - dùng để tính chiều dài cung $L[a,b]$ , bạn đọc xem chi tiết ở phần II của bài viết này .
Thực hành với $c =1,a =1, b= 2$ ta có :
+Độ cong $C(x)= \frac{2Cx^3+x}{[4C^2x^4+x^2(1-4C)+1]^{3/2}}$
Xem WA trực tuyến
http://goo.gl/al2CAh
Ví dụ : $C = 1 , x = 1/2$ ta có $C= \frac{3}{\sqrt{2}}$ ( xem
http://goo.gl/oYtwVv )
Procedure dưới đây tác giả viết bằng MapleV có tên là
docongbouguer - dùng để tính độ cong C(x) , các bạn xem chi tiết ở phần II của bài viết này .
Ví dụ với $C =1 , x =1/2$ ta có :
+Chu vi
+Diện tích
Các đường liên hợp
Xem
http://youtu.be/pdnY7jy-Wz4
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y = c.x^2 - lnx$
y = c*x^2 - log(x)
Nhập liệu bằng
http://graphsketch.com/
Thực hành với c = 0.25 , 0.5 , 1 , 2 , 3 , 4
Xem trực tuyến :
http://goo.gl/6WSqtQ
1.5 Quadratrix of Hippias (Đường bốn đỉnh Hippias) [47]
A . Khái niệm .
-Hippias xứ Elis phát hiện ra đường cong Quadratrix năm 430 trước Công nguyên khi ông giải quyết bài toán chia ba một góc và bình phương đường tròn . Dinostratus tiếp tục nghiên cứu bài toán này vào 350 trước Công nguyên .Tính chất quan trọng nhất của đường cong này về sau được sử dụng để phân chia một góc bất kỳ thành một số các góc nhỏ bằng nhau .
-Một cách khái quát các đường quadratrix hoặc trisectrix Hippias (cũng gọi là quadratrix Dinostratos ) là một đường cong , được tạo ra bởi một chuyển động thẳng đều. Đây là một trong những ví dụ cổ xưa nhất về tính chất điểm động học đường cong, đó là quỹ tích của một điểm lưu động .
-Xét một hình vuông ABCD với 1/4 thứ nhất của đường tròn tâm A bán kính AB. Cho E là một điểm chuyển động với vận tốc góc không đổi trên cung tròn DB . Gọi F là điểm lưu động với vận tốc không đổi từ D đến A trên cạnh AD . Hai điểm E và F bắt đầu cùng lúc tại D và đến cùng một lúc tại B . Khi đó quadratrix được định nghĩa là quỹ tích của các giao điểm S của đường song song với AB qua F và tia bán kính AE .
( xem hình )
Nếu đặt hình vuông ABCD trên đây vào hệ trục Descartes với cạnh AB nằm trên trục hoành và đỉnh A là gốc tọa độ . Khi đó các quadratix được mô tả bằng một đường cong phẳng có phương trình tham số :
$x= \frac{2a}{\pi}tcot(t)$
$y=\frac{2a}{\pi}t$
Hình động dưới đây mô tả quỹ tích điểm S là đường cong quadratrix Hippias .

-Bằng cách khử tham số t giữa x và y :
$\frac{y}{x}=tan(t)=tan[\pi y / (2a)] \Leftrightarrow y = x.tan[\pi y / (2a)]$
Đổi trục bằng cách thay $x = y$ ta có $x=y.tan[\pi x / (2a)]$ hay $y=x.cot[\pi x / (2a)]$
+Chiều dài cung
Procedure dưới đây tác giả viết bằng MapleV có tên là
cdcungquadratrix - dùng để tính chiều dài cung $L[a,b]$ tương ứng với hàm $y=x.cot[\pi x / (2a)]$ - xem chi tiết ở phần II .
Thực hành với $A =1,a =1.5, b= 1.8$ ta có :
+Độ cong
Procedure dưới đây tác giả viết bằng MapleV có tên là
docongquadratrix - dùng để tính độ cong C(x) tương ứng với hàm $y=x.cot[\pi x / (2a)]$ - xem chi tiết ở phần II .
Thực hành với $A =1,x =2.5$ ta có :
Độ cong C(t) tương ứng với phương trình tham số
$x= \frac{2a}{\pi}tcot(t)$
$y=\frac{2a}{\pi}t$ là $C(t)= \frac{\pi (sint - tcost}{a(1-2t.cost +t^2csc^2t)^{3/2}}$
+Chu vi
+Diện tích
Các đường liên hợp
Xem
http://youtu.be/F30Wqy3lxeE
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$x=y.tan[\pi x / (2a)]$
hay
$y = x.cot(\pi.x/(2a))$
y = x*cot(Pi*x/(2*a))
Phương trình tham số của đường cong trong hệ trục tọa độ Descartes :
$x= \frac{2a}{\pi}tcot(t)$
$y=\frac{2a}{\pi}t$
Phương trình đường cong trong hệ tọa độ cực:
$r = 2aθ / (\pi sin(θ))$
r = 2*a*θ / (Pi*sin(θ))
Nhập liệu bằng DESMOS , chọn giá trị cho thanh trượt a .

Xem trực tuyến
https://www.desmos.com/calculator/idbnmiuu4b
1.6 Rhodonea Curves (Đường cong Rhodonea) [48]
A . Khái niệm .
+Đường cong Rhodonea được đặt tên bởi nhà toán học người Ý Guido Grandi giữa năm 1723 và 1728.
Đường bông hồng (rose) hoặc đường cong rhodonea là một đường hình sin vẽ trong tọa độ cực . Lưu ý rằng những đường cong này đều có thể được biểu diễn một cách tương tự bằng một phương trình trong hệ tọa độ cực có dạng $r=cos(kθ)$
hoặc dưới dạng phương trình tham số Descartes
$x=cos(kt).cost$
$y=cos(kt).sint$
+Nếu k là một số nguyên , đường cong sẽ có dạng hoa hồng với số cánh hoa là :
* 2 k cánh hoa nếu k chẵn , và
* k cánh hoa nếu k lẻ ( xem hình sau )
+Khi k chẵn , toàn bộ đồ thị của đường hoa hồng sẽ xuất hiện đúng một lần khi giá trị của θ thay đổi từ 0 đến 2π.
Khi k là số lẻ, điều này sẽ xảy ra trên khoảng giữa 0 và π .
Nói chung, điều này sẽ xảy ra trên mọi khoảng thời gian 2π cho k chẵn , và π cho k lẻ .
+Các trường hợp đặc biệt
-Nếu k kết thúc với 1/2 ( nghĩa là k+1/2 ; ví dụ: 0.5, 2.5), các đường cong sẽ được hoa hồng hình với 4 k cánh hoa.
-Nếu k kết thúc với 1/6 ( nghĩa là k+1/6 hoặc 5/6 và lớn hơn 1 ; ví dụ: 1,16666667, 2,8333333), đường cong sẽ có hình hoa hồng với 12k cánh hoa.
-Nếu k kết thúc bằng 1/3 ( nghĩa là k+1/3 và lớn hơn 1 ; ví dụ: 1,333333, 2,333333), đường cong sẽ có:
3k cánh hoa nếu k chẵn , và
6k cánh hoa nếu k là số lẻ.
-Nếu k kết thúc bằng 2/3 ( nghĩa là k+2/3 và lớn hơn 1 ; ví dụ: 1,666667, 2,666667), đường cong sẽ có:
6k cánh hoa nếu k chẵn , và
3k cánh hoa nếu k là số lẻ.
-Nếu k là số hữu tỷ , thì đường Rhodonea khép kín và có chiều dài hữu hạn.
-Nếu k là số vô tỷ , thì đường cong không đóng kín và có chiều dài vô hạn. Hơn nữa, đồ thị của hoa hồng trong trường hợp này tạo thành một tập hợp dày đặc (nghĩa là , nó tiến gần đến tất cả các điểm trong dĩa đơn vị ).
Vì $sin(kθ)=cos(\pi/ 2 - kθ) = cos[-k(θ- \frac{\pi}{2k})]= cos[k(θ- \frac{\pi}{2k})]$ nên các đường cong cho bởi phương trình cực $r=sin(kθ)$ và $r=cos(kθ)$ là giống hệt nhau sau một vòng quay $\frac{\pi}{2k}$ radian .
Dưới đây là bộ sưu tập các đường cong thuộc họ rhodonea.
+Chiều dài cung
Procedure dưới đây tác giả viết bằng MapleV có tên là
cdcungrose - dùng để tính chiều dài cung $L[a,b]$ tương ứng với hàm $r = A.sin(kθ)$ - xem chi tiết ở phần II .
Thực hành với $A =1,a =0, b= 2 \pi$ ta có :
Xem WA trực tuyến
http://goo.gl/xU7B7Q
+Độ cong
Procedure dưới đây tác giả viết bằng MapleV có tên là
docongrose - dùng để tính độ cong C(θ) tương ứng với hàm $r = A.sin(kθ)$ - xem chi tiết ở phần II .
Thực hành với $A =3,k= 2 , θ= \pi/6 $ ta có :
+Diện tích
Diện tích giới hạn bởi đường rose khép kín được tính bởi công thức
$S= \frac{1}{2} \int (r^2)dθ $
-Khi $k=2m$ (chẵn ) ta có $S= 1/2 \int_{0}^{2 \pi} [Asin(kθ)]^2=\frac{1}{4}\left [ -\frac{sin(4m\theta )}{4m} + \theta \right ]A^2 $
Hay $S=\frac{\pi A^2}{2}$
-Khi $k=2m+1$ (lẻ ) ta có $S= 1/2 \int_{0}^{\pi} [Asin(kθ)]^2=\frac{1}{4}\left [ -\frac{sin(2(2m+1)\theta )}{2(2m+1)} + \theta \right ]A^2 $
Hay $S=\frac{\pi A^2}{4}$
Trong mô hình dưới đây các bạn chọn giá trị cho các tham số r , p , q và click vào Ctapt .
Xem
https://www.geogebratube.org/material/iframe/id/44498
Các đường liên hợp
Xem
http://youtu.be/RcyflzxfRB8
B. Phương trình .
Phương trình tham số của đường cong trong hệ tọa độ Descartes
$x=cos(kt).cost$
$y=cos(kt).sint$
Phương trình đường cong trong hệ tọa độ cực:
$r = A.sin(kθ)$ hay $r = A.cos(kθ)$
r = A*sin(kθ)
Nhập liệu bằng SMS , các bạn truy cập trang
http://graph.seriesmathstudy.com/
Click vào Start GraphFunc . Thực hành vẽ đồ thị hàm Rhodonea ( Rose) với $A=3 , k =5$ khoảng vẽ từ 0 đến $\pi$ . SMS có chức năng tính chiều dài cung , diện tích giới hạn của đường cong ; chọn các giá trị của t từ ... đến ... , sau đó click vào
Find Area để tìm diện tích và
Arc Length để tìm chiều dài cung . Với những tham số trên , ta tìm được
+Chiều dài cung trên đoạn $[0, \pi]$ là $L \approx 31.51507$
+Diện tích $S \approx 7.06858$ ( xem hình động dưới đây - Click vào ảnh để phóng to)
1.7 Right strophoid (Đường strophoid vuông) [49]
A . Khái niệm .
Isaac Barrow đã nghiên cứu về các đường strophoid và đề cập đến trong các công trình khoa học vào năm 1670.
Trước đó Torricelli cũng đã từng mô tả đường cong này trong một số văn kiện của ông khoảng năm 1645 . Tác giả Roberval tìm thấy đường strophoid là quỹ tích thu được của tiêu điểm của một hình conic khi cho mặt phẳng cắt hình nón quay quanh tiếp tuyến tại đỉnh của nó.
Tên gọi strophoid vuông này được đề xuất bởi Montucci vào năm 1846. Các strophoid tổng quát có phương trình $r= a.sin(\alpha - 2θ) / sin(\alpha - θ)$ .
-Cho trước hai điểm O và F , đường cong strophoid vuông có đỉnh là F , tâm O là quỹ tích các điểm M của tia ( D ) qua F thỏa mãn PM = PO , với P là điểm giao điểm của tia ( D ) với đường vuông góc với OF tại O (gọi là trục (T) của strophoid) .
Đây là một trường hợp đặc biệt của đường cong strophoid tổng quát có phương trình trong hệ tọa độ cực là

với

Tiệm cận đứng là
và phương trình đường cong trong hệ tọa độ Descartes có dạng

-Cách xây dựng đường strophoid tổng quát :
Trong mặt phẳng cho hai điểm O và F cố định và đường cong (T) , từ F dựng tia (D) cắt (T) tại điểm P . Quỹ tích các điểm M trên tia (D) thỏa mãn tính chất PM = PO khi tia (D) quay quanh F gọi là đường strophoid . Khi OF trực giao với (T) ta nói đường cong này là strophoid vuông .
Một vài hình dạng biến thể của strophoid tổng quát như sau đây
-Xét đường cong strophoid tổng quát , khi $\alpha = 0 $ thay vào phương trình tọa độ cực ta có phương trình đường strophoid vuông : $r = a.cos(2θ)/cos(θ)$
Trong hình động dưới đây nếu OF _|_ trục (T) của strophoid ( màu xanh) ta sẽ thu được đồ thị của strophoid vuông .
- Đường strophoid vuông (màu đỏ) cũng là quỹ tích trực tâm H cùa tam giác ABC , trong đó điểm A và B cố định và điểm C lưu động trên đường tròn có tâm là A , bán kính là AB ( xem hình )
+Một cách nhìn khác về strophoid vuông : Đường cong strophoid vuông là trường hợp đặc biệt khi
$a=c ; b=0$ của đường cong kieroid có phương trình tổng quát là

+Chiều dài cung : từ phương trình tham số của strophoid
$x=a. \frac{a^2-t^2}{a^2+t^2}$
$y=-t. \frac{a^2-t^2}{a^2+t^2}$
Công thức chiều dài cung là
$L(t)=ika[(2 \sqrt{2}-3)E(\phi_0,k^2)+2kF(\phi_0,k^2)+4 \Pi(k^2,\phi_0,k^2)]$
với $k=1+ \sqrt{2}$ và $\phi_0=i.arcsinh(kt/|a|)$
Trong đó $E(\phi,k) , F(\phi,k) , \Pi(\phi,k,n)$ là các tích phân elliptic không đầy đủ loại 1 , 2 và 3 .
+Độ cong $K(t)=-4a^3(a^2+3t^2)/(a^4+6a^2t^2+t^4)^{3/2}$
+Chu vi .
+Diện tích vòng lặp
$S=1/2. \int_{-a}^{a}(x'y-xy')dt=1/2 . \int_{-a}^{a}\left ( \frac{a^2-t^2}{a^2+t^2} \right )^2dt =\frac{(4-\pi)c^2}{2} $
Tính toán chiều dài cung , độ cong , diện tích từ phương trình strophoid vuông trong hệ tọa độ cực :
-Procedure dưới đây tác giả viết bằng MapleV có tên là
cdcungrightstrophoid - dùng để tính chiều dài cung $L[a,b]$ tương ứng với hàm $r = A.cos(2θ)/cos(θ)$ - xem chi tiết ở phần II .
Thực hành với $A =3,a =0, b= \pi /4$ ta có :
-Procedure dưới đây tác giả viết bằng MapleV có tên là
docongrightstrophoid
- dùng để tính độ cong C(θ) tương ứng với hàm $r = A.cos(2θ)/cos(θ)$ - xem chi tiết ở phần II .
Thực hành với $A =3, θ = \pi /4$ ta có :
-Hình động minh họa cách xây dựng đường strophoid vuông
Xem chi tiết
https://www.geogebratube.org/material/iframe/id/108015
Các đường liên hợp
Xem
http://youtu.be/nZdK4A6wxXc
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y^2=x^2.(a-x)/(a+x)$
y^2=x^2*(a-x)/(a+x)
Phương trình tham số của đường cong trong hệ tọa độ Descartes:
$x=a. \frac{a^2-t^2}{a^2+t^2}$
$y=-t. \frac{a^2-t^2}{a^2+t^2}$
Phương trình đường cong trong hệ tọa độ cực:
$r = A.cos(2θ)/cos(θ)$
r = A*cos(2*θ)/cos(θ)
Nhập liệu bằng MapleV với lệnh
implicitplot(y^2=x^2*(Ad-x)/(Ad+x),x=-Ad-1..Ad+1,y=-Ad-1..Ad+1,grid=[250,250],color=green,thickness=3);
Thực hành với Ad = 3 , 4 , 5
Nhập liệu bằng DESMOS với y^2=x^2*(a-x)/(a+x) , chọn giá trị cho thanh trượt a
hoặc r = a*cos(2*θ)/cos(θ)
Xem trực tuyến
https://www.desmos.com/calculator/v6c2ileqi0
Các bạn có thể dùng SMS để vẽ đồ thị strophoid vuông , tình toán chiều dài cung và diện tích giới hạn . Truy cập vào
http://graph.seriesmathstudy.com/ nhập liệu với $ A*cos(2*t)/cos(t)$ , chọn các giá trị của t từ ... đến ... , sau đó click vào
Find Area để tìm diện tích và
Arc Length để tìm chiều dài cung .
Thực hành với $A =3,a =0, b= \pi /4$ ta có giá trị của S và L tương tự như các procedure tác giả đã viết bằng MapleV ( xem hình động minh họa sau đây - click vào hình để phóng to ) .
1.8 Serpentine Curve (Đường uốn khúc serpentine) [50]
A . Khái niệm .
- De L'Hôpital và Huygens đã nghiên cứu về đường uốn khúc serpentine trước tiên vào năm 1692 . Sau đó , đến năm 1701 Newton bắt đầu khảo sát chi tiết và đặt tên chính thức cho đường cong này .
Đường serpentine thuộc lớp phân loại các đường bậc 3 được viết trong cuốn sách Curves (Các đường cong) của Sir Isaac Newton trong Tuyển tập Lexicon Technicum (Tự điển kỹ thuật), Nhà xuất bản John Harris in tại London năm 1710.
Isaac Newton kết luận rằng các đường cong $f(x,y)=0 $, trong đó $f(x,y)$ là hàm bậc 3, có thể được chia thành một trong bốn dạng chuẩn. Đường cong serpentine thuộc phân lớp của dạng đầu tiên có phương trình tổng quát là $y(xy+e)=ax^3+bx^2+cx+d$
-Trong hệ trục tọa độ Oxy xét đường tròn tâm $C(a,0)$ và điểm $B(0,b)$ cố định trên trục tung với $a>b>0$ . Gọi P là điểm lưu động trên nửa đường tròn trên ( các tọa độ $x_P,y_P \geq 0$ ) . Qua B dựng đường thẳng song song trục hoành cắt tia OP tại D . Từ D dựng đường vuồng góc với trục hoành và từ P dựng đường vuông góc với trục tung . Hai đường này cắt nhau ở điểm M . Khi P chạy trên cung tròn $\frown APO$ thì quỹ tích của M là nửa phần trên đường cong uốn khúc serpentine .
( xem hình )
-Đặt $t=\measuredangle AOP$ ta có $2t=\measuredangle ACP$ .
Tim tọa độ điểm P như sau :
$x_P= OC+CP = a + CP.cos2t = a+a.cos2t$
$y_P=a.sin2t$
Tim tọa độ điểm M như sau :
$x_M = Om = b.cott$
$y_M = y_P = a.sin2t$ . Do đó ta xác định được điểm tọa độ của điểm $M (b.cott , a.sin2t)$ .
Khử tham số t giữa 2 tọa độ điểm M :
Từ $x= b.cott $ bình phương hai vế và đổi $cott = \frac{cost}{sint}$ thu được $x^2.sin^2t=b^2cos^2t$
hay $x^2.(1-cos^2t)=b^2cos^2t$ . Khi đó $x^2=(x^2+b^2).cos^2t$ (1)
Trong mô hình trên để ý rằng
$\frac{Om}{Op}=\frac{Dm}{Pp} = \frac{x_M}{x_P}=\frac{y_D}{y_P}=\frac{x_M}{a+acos2t} =\frac{b}{y_M}$ , nói cách khác $\frac{x}{a+acos2t} =\frac{b}{y}$
nên $xy=b(a+acos2t) = 2ab.cos^2t$ như vậy $cos^2t= \frac{xy}{2ab}$
Thay vào (1) ta có $x^2=(x^2+b^2).cos^2 t= (x^2+b^2). \frac{xy}{2ab}$
Rút gọn hai vế thu được $y= 2abx / (x^2+b^2)$
Bằng cách thay đổi các hằng số phương trình serpentine trong hệ tọa độ Descartes có thể viết dưới dạng
$y.(x^2+ab) - a^2.x=0 , ab > 0$ đây chính là phương trình dạng hàm ẩn biểu diễn của đường serpentine .
+Chiều dài cung : Với phương trình đường cong trong hệ tọa độ Descartes :
$y = 2abx / (x^2+b^2)$
Công thức chiều dài cung là $L[\alpha , \beta] = \int_{\alpha }^{\beta }\sqrt{1+y'^2}dx$
Procedure dưới đây tác giả viết bằng MapleV có tên là
cdcungserpentine - dùng để tính chiều dài cung $L[a,b]$ tương ứng với hàm $y = 2ABx / (x^2+B^2)$ - xem chi tiết ở phần II .
Thực hành với $A =1, B = 1 , a =0, b= 1$ ta có :
+Độ cong
Procedure dưới đây tác giả viết bằng MapleV có tên là
docongserpentine - dùng để tính độ cong C(x) tương ứng với hàm $y = 2ABx / (x^2+B^2)$ - xem chi tiết ở phần II .
Thực hành với $A =1, B =1 ,x =2.5$ ta có :
+Chu vi
+Diện tích
Procedure dưới đây tác giả viết bằng MapleV có tên là
dtichserpentine - dùng để tính diện tích giới hạn bởi C(x) trên đoạn $[a,b]$ tương ứng với hàm $y = 2ABx / (x^2+B^2)$ - xem chi tiết ở phần II .
Thực hành với $A =1, B =1 , a = 0 , b = 1$ ta có :
-Trong mô hình dưới đây điểm M chạy trên đường tròn tâm C thì P chạy trên đường serpentine (màu vàng) và có tiếp tuyến tương ứng tại P (màu cam) .
Xem chi tiết
https://www.geogebratube.org/material/iframe/id/32649
Các đường liên hợp
Xem
http://youtu.be/EpgrDg_QlVo
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$y(x^2+ab)-a^2.x=0 , ab > 0$
hay $y = 2ABx / (x^2+B^2)$
y*(x^2+a*b)-a^2*x=0 , ab > 0
Phương trình tham số của đường cong trong hệ tọa độ Descartes :
$x= b.cott$
$y= a.sin2t$
-Sử dụng công cụ trực tuyến SMS để vẽ đồ thị serpentine , tính toán chiều dài cung và diện tích giới hạn . Truy cập vào
http://graph.seriesmathstudy.com/ nhập liệu với $y = 2ABx / (x^2+B^2)$ , chọn các giá trị của t từ ... đến ... , sau đó click vào
Find Area để tìm diện tích và
Arc Length để tìm chiều dài cung .
Thực hành với $A =1 , B = 1 ,a =0, b= 1$ ta có giá trị của $S \approx 0.69315$ và $L \approx 1.50126$ tương tự như các procedure tác giả đã viết bằng MapleV ( xem hình động minh họa sau đây - click vào hình để phóng to ) .
-Nhập liệu bằng DESMOS , chọn giá trị cho thanh trượt a .
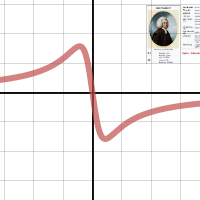
Xem trực tuyến
https://www.desmos.com/calculator/fa0koolzg5
1.9 Sinusoidal Spirals (Đường xoắn ốc hình sin) [51]
A . Khái niệm .
-Đường xoắn ốc hình sin được Maclaurin khảo sát đầu tiên , trong phương trình biểu diễn đường cong tham số n là hữu tỷ . Phương trình đường xoắn ốc hình sin trong hệ tọa độ cực là :
$r^n= a^n.cos(nθ)$
-Một số dạng chuẩn xảy ra như trường hợp đặc biệt của đường xoắn ốc hình sin như sau đây :
Nếu $n = 1/3$ ta có phương trình Cayley sextic .
Nếu $n = – 1 / 3$ ta có phương trình bậc 3 Tschirnhausen .
Nếu $n = 1/2$ ta có phương trình cardioid.
Nếu $n = – 1 / 2$ ta có phương trình parabola.
Nếu $n = – 1$ ta có phương trình đường thẳng.
Nếu $n = 1$ ta có phương trình đường tròn.
Nếu $n = – 2$ ta có phương trình hyperbola.
Nếu $n = 2$ ta có phương trình lemniscate của Bernoulli.
-Về tổng quát : Đồ thị đường xoắn hình sin đối xứng qua trục cực .
-Khi $n > 0$ đường xoắn ốc hình sin đi qua cực và nội tiếp đường tròn bán kính a . Khi $n < 0$ vector bán kính cực của đường cong có giá trị lớn tùy ý , đường cong không đi qua cực .
-Khi $n=p/q$ với p, q là 2 số nguyên tố cùng nhau , đồ thị có p trục đối xứng cùng đi qua cực . Nếu $n=p/q >0$ đồ thị có p nhánh cắt nhau .
-Khi $n \in Z^{+}$ , vector bán kính cực của đường cong là hàm tuần hoàn có chu kỳ $2 \pi /n$ , góc cực $θ \in [0, 2 \pi]$
đường cong có n nhánh , mỗi nhánh nằm trong góc $\pi / n$.
-Khi $n \in Z^{-}$ , đường cong có $ |n| $ nhánh vô hạn .
Các đường xoắn ốc sin : $r^n=a^n.cos(nθ)$ đảo ngược thành : $r^n=a^n/cos(n.θ)$ nếu tâm của phép nghịch đảo đặt tại điểm cực.
( xem hình minh họa dưới đây )
-Với $n \in Q^{+}$
-Với $n \in Q^{-}$
+Chiều dài cung
-Procedure dưới đây tác giả viết bằng MapleV có tên là
cdcungsinspiral - dùng để tính chiều dài cung $L[a,b]$ tương ứng với hàm $r = A.cos(nθ)^{1/n}$ - xem chi tiết ở phần II .
Thực hành với $A =1 , n = 3 ,a =0, b= \pi /2$ ta có :
Xem tính toán bằng WA trực tuyến
http://goo.gl/c2mGNV
+Độ cong
+Chu vi
+Diện tích
Xem WA trực tuyến
http://goo.gl/scWFIc
Ví dụ với $n=3 , a=1$ ta có
Diện tích $S \approx 0.560126 $
http://goo.gl/9qk9CW
-Procedure dưới đây tác giả viết bằng MapleV có tên là
dtichsinspiral- dùng để tính diện tích giới hạn bởi đường cong sin xoắn ốc $r = A.cos(nθ)^{1/n}$ trên đoạn $[a,b]$ - xem chi tiết ở phần II .
Thực hành với $A =1, n = 3 , a =0 , b= \pi /2$ ta có :
-Bạn đọc có thể dùng công cụ SMS trực tuyến để tính diện tích và chiều dài cung
Truy cập vào
http://graph.seriesmathstudy.com/ nhập liệu với $r = A.cos(nt)^{1/n}$ , chọn các giá trị của t từ ... đến ... , sau đó click vào
Find Area để tìm diện tích và
Arc Length để tìm chiều dài cung .
Thực hành với $A =1 , n = 3 ,a =0, b= \pi /2$ ta có giá trị của $S \approx 0.56013$ và $L \approx 3.64306$ tương tự như WA ( xem hình động minh họa sau đây - click vào hình để phóng to ) .
Các đường liên hợp
Xem
http://youtu.be/cAHuU22lk8U
B. Phương trình .
Phương trình đường cong trong hệ tọa độ cực:
$r^p=a^p.cos(pθ)$
r^p=a^p*cos(p*θ)
Nhập liệu bằng SMS với r = A*cos(nt)^(1/n) .
Thực hành với $A =1 , n = 3 $
Nhập liệu bằng GP với r = A*cos(nt)^(1/n) .
Thực hành với $A =1 , n = 3 $ (xem hình động sau )
1.10 Spirals of Archimedes (Đường xoắn Archimedes) [52]
A . Khái niệm .
-Khoảng năm 225 trước Công nguyên Archimedes đã nghiên cứu về đường xoắn ốc này và ông đã ghi lại các thông tin trong tác phẩm " Về các đường xoắn ốc ". Công trình này sau đó được Conon – một người bạn của Archimedes - tiếp tục khảo sát . Nếu cực là tâm của phép nghịch đảo, đường xoắn ốc Archimedes biến đổi thành đường xoắn ốc hyperbolic .
-Các tính chất toán học và ứng dụng vật lý của đường xoắn Archimedes khá đa dạng , từ bài toán chia 3 một góc đến chuyển động tay cam , thiết bị bơm và máy nén khí ( xem hình ) .
 |
| Mô hình máy bơm quay tay . |
 |
| Cơ chế hoạt động của máy nén khí . |
 |
| Chuyển động chất điểm trên đường xoắn ốc Archimedes . |
 |
| Giải thích cách chia một cung theo tỷ số cho trước |
Đường xoắn Archimedes là quỹ tích của các điểm tương ứng với các vị trí theo thời gian khi di chuyển ra khỏi một điểm cố định với một tốc độ không đổi dọc theo một đường thẳng quay với hằng số vận tốc góc . Trong hệ tọa độ cực $( r , θ )$ quỹ tích này có thể được mô tả bởi phương trình
$r = b + aθ , a,b \in R $ . Thay đổi thông số b sẽ biến đổi vị trí điểm cực của đường xoắn ốc, trong khi a liên quan khoảng cách giữa các cung kế tiếp nhau .
Xem trực tuyến
https://www.desmos.com/calculator/joeqvtrlkl
 |
| Thay đổi b - biến đổi vị trí điểm cực . |
 |
| Thay đổi a - khoảng cách giữa các cung |
Một số tính chất đặc trưng :
-Mọi tia bất kỳ xuất phát từ điểm gốc đều cắt những cung kế tiếp của đường xoắn ốc Archimedes
$r = b + aθ$ tại những điểm theo cùng một khoảng cách không đổi (bằng $2 \pi a$ nếu θ tính bằng radian ), do đó còn có tên " đường xoắn ốc số học" ( cấp số cộng ) .
-Ngược lại điều này những khoảng cách tương tự như vậy trên đường xoắn ốc logarit $r = b.e^{aθ}$ lại tạo thành một cấp số nhân .
-Đường xoắn ốc Archimedean có hai nhánh nối nhau tại điểm gốc , một nhánh cho $θ > 0$ và một cho $θ < 0$ , đối xứng nhau qua trục Oy .
-Họ đường cong xoắn ốc Archimedes có phương trình tổng quát trong hệ tọa độ cực là $r = b + aθ^{1/c}$ . Các trường hợp đặc biệt
Nếu $c = 1$ ta có đường xoắn ốc Archimedes .
Nếu $c = -1$ ta có đường xoắn ốc hyperbolic .
Nếu $c = 2$ ta có đường xoắn ốc Fermat .
Nếu $c = -2$ ta có đường xoắn ốc Lituus .
Xem chi tiết
https://www.desmos.com/calculator/0do4rfuoae
Với phương trình đường xoắn Archimedes $r = a.θ$
+Chiều dài cung
$L(θ) = \frac{a}{2} [θ \sqrt{1+θ^2}+ln(θ+\sqrt{1+θ^2})]$
-Các bạn có thể dùng công cụ SMS trực tuyến để tính diện tích và chiều dài cung
Truy cập vào
http://graph.seriesmathstudy.com/ nhập liệu với $r = A.t$ , chọn các giá trị của t từ ... đến ... , sau đó click vào
Find Area để tìm diện tích và
Arc Length để tìm chiều dài cung .
Thực hành với $A =1 , a =0, b= \pi $ ta có giá trị của $S \approx 20.67085$ và $L \approx 12.21961$ ( xem hình minh họa sau đây - click vào hình để phóng to ) .
+Độ cong
$K(θ) = \frac{2+θ^2}{a(1+θ^2)^{3/2}}$
+Chu vi
+Diện tích
Thực hành với các procedure do tác giả viết bằng Maple V có tên
cdcungarcspiral ,
docongarcspiral ,
dticharcspiral để tính chiều dài cung , độ cong và diện tích giới hạn . Nhập liệu các tham số $A=2 , B = 0 , a = 0 , b = \pi , θ = \pi $ ta nhận được kết quả sau :
Các đường liên hợp
Xem
http://youtu.be/AyskWTGNopY
B. Phương trình .
Phương trình đường cong trong hệ tọa độ cực:
$r = b + a.θ$
r = b + a*θ
Hoặc $r=b+a \theta ^{1/c}$
Nhập liệu bằng DESMOS chọn giá trị cho thanh trượt a , b và c .
Thực hành với $ c = 1 , a = 2 , b = 0$
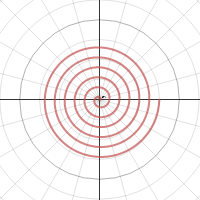
Xem trực tuyến
https://www.desmos.com/calculator/4j41rzdkxb
1.11 Spiric Section (Đường tiết diện xoắn) [53]
A . Khái niệm .
-Khoảng năm 150 trước Công nguyên nhà toán học Hy Lạp Perseus khảo sát các đường tiết xoắn - spiric sections . Đây là các đường cong chu vi của tiết diện tạo bởi một hình xuyến và mặt phẳng song song với đường thẳng đi qua các tâm của lỗ xuyến có phương trình đường cong trong hệ tọa độ Descartes là
$(r^2-a^2+c^2+x^2+y^2)^2=4.r^2.(x^2+c^2)$
Hình động minh họa các đường tiết diện xoắn ( xem hình )
-Trong phương trình của đường cong được đưa ra ở trên , hình xuyến được hình thành từ một đường tròn bán kính là a có tâm quay theo một đường tròn bán kính r. Tham số c là khoảng cách từ tâm của hình xuyến đến tiết diện .
Nếu $r =0$ đồ thị đường cong là rỗng .
Nếu $c = 0$ đường cong gồm hai đường tròn có bán kính là a, có tâm tại I(r, 0) và J(-r, 0).
Nếu $c = r + a$ , đường cong suy biến về một điểm, thường gọi là gốc .
Nếu $c > r + a$ , thì không có một điểm nào nằm trên đường cong .
Sử dụng DESMOS để minh họa đồ thị đường tiết diện xoắn với các tham số a , c , r
https://www.desmos.com/calculator/cdjd7crj4r
-Gọi bán kính từ trung tâm của lỗ đến trung tâm của ống xuyến là R (c) , và bán kính của ống xuyến là r a . Hình xuyến trong không gian Oxyz có phương trình tham số là
$x=(R+r.cosv)cosu$
$y=(R+r.cosv)sinu$
$z=r.sinv$ với $u,v \in [0,2 \pi)$ .
Ba loại hình xuyến, được gọi là xuyến tiêu chuẩn , là có thể xẩy ra , tùy thuộc vào kích thước tương đối của r và R .
Khi $R > r$ tương ứng với hình xuyến vòng (hiển thị ở trên) .
Khi $R = r$ tương ứng với một xuyến sừng có tiếp tuyến chung tại gốc O(0, 0, 0) .
Khi $R < r$ tương ứng với xuyến trục ( có một trục chính ) (Theo Pinkall 1986).
Nếu không có đặc điểm kỹ thuật nào khác được thực hiện, thì "xuyến" được hiểu là hình xuyến vòng . Ba xuyến tiêu chuẩn được minh họa dưới đây, với hình ảnh đầu tiên cho thấy xuyến đầy đủ, thứ hai là xuyến nửa dưới bị cắt bởi mặt phẳng Oxy , và thứ ba là tiết diện ngang với mặt phẳng đi qua trục Oz .
Các dạng của đường tiết diện xoắn cắt bởi mặt phẳng song song trục Oz được mô tả như sau
-Cách xây dựng đường tiết diện xoắn :
Trong hệ trục không gian Oxyz như hình vẽ , xét đường tròn tâm I trong mặt phẳng (OyN) ( màu xanh ) bán kính r và OI = a . Phương trình đường tròn này là $(xM - a )^2 + yM^2 = r^2$ (1)
Trong mặt phẳng (Oxz) ta có $ON = xM$ thỏa mãn $xM^2=ON^2=x^2+z^2$ hay $xM= \sqrt{x^2+z^2}$ (2)
Khai triển (1) và thay (2) vào thu được
$x^2+z^2-2a.\sqrt{x^2+z^2}+a^2+y^2=r^2$ . Chuyển biểu thức chứa căn sang một vế và bình phương lên ta có
$(x^2+z^2+a^2+y^2-r^2)^2=4a^2.(x^2+z^2)$
Nếu ta cắt xuyến bằng một mặt phẳng song song với (Oxy) với $z = c$ khi đó phương trình đường tiết diện xoắn trở thành
$(x^2+c^2+a^2+y^2-r^2)^2=4a^2.(x^2+c^2)$
Thay $r = a$ ta có
$(r^2-a^2+c^2+x^2+y^2)^2=4r^2.(x^2+c^2)$
Với $(x^2+c^2+a^2+y^2-r^2)^2=4a^2.(x^2+c^2)$ ta có
$y = \pm \sqrt{r^2-(\sqrt{x^2+c^2}-a)^2}$ . Trong các phần tính toán dưới đây ta chọn
$y = + \sqrt{r^2-(\sqrt{x^2+c^2}-a)^2}$
+Chiều dài cung
Dùng công cụ trực tuyến SMS vẽ đổ thị , tính chiều dài cung và diện tích giới hạn
Thực hành với $r = 3 ; c = 2 ; a =5 ; x \in [1,4] $ ta có chiều dài cung $L \approx 3.55706$ và diện tích $S \approx 6.86107$ (xem hình )
+Độ cong
+Chu vi
+Diện tích
Các đường liên hợp
Xem
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$(r^2-a^2+c^2+x^2+y^2)^2=4r^2.(x^2+c^2)$
(r^2-a^2+c^2+x^2+y^2)^2=4*r^2*(x^2+c^2)
Hay
$(x^2+c^2+a^2+y^2-r^2)^2=4a^2.(x^2+c^2)$
(x^2+c^2+a^2+y^2-r^2)^2=4a^2.(x^2+c^2)
Nhập liệu bằng DESMOS với
$y=\sqrt{r^2-(\sqrt{x^2+c^2}-a)^2}$ và
$y= - \sqrt{r^2-(\sqrt{x^2+c^2}-a)^2}$
Chọn giá trị cho thanh trượt r , c , a .
Xem trực tuyến
https://www.desmos.com/calculator/b9gfg98txj
II . Các lệnh đồ họa trong trình ứng dụng Maple .
Dưới đây là nội dung tiếp theo mục II - phần 6 trình bày các thủ tục và các tùy chọn đồ họa 3D của trình ứng dụng Maple V .
2.1 Đồ thị 3D .
2.1.4 Hình đa diện trong hệ tọa độ không gian .
a. Cấu trúc lệnh .
> polyhedraplot(L,options);
Tham số
L - là tập hợp (danh sách) các điểm trong 3D .
Mô tả:
-Lệnh polyhedraplot được sử dụng để vẽ các điểm với các khối đa diện ba chiều. Các điểm được vẽ từ các tập hợp hoặc danh sách L. L có dạng như sau [[x1, y1, z1], [x2, y2, z2], ..., [xn, yn, zn]]. Nếu chỉ có một điểm, L có biểu diễn đơn giản là [x, y, z].
-Hai tùy chọn cụ thể cho lệnh này là polyscale = <constant> và polytype = <set>, trong đó polyscale kiểm soát kích thước của mỗi đa diện, và polytype là một trong các tùy chọn {tứ diện, bát diện , khối sáu mặt, khối mười hai mặt, khối hai mươi mặt (tetrahedron,octahedron,hexahedron,dodecahedron,icosahedron)}. Quy mô mặc định là là polyscale = 1, và polytype = tứ diện.
-Các tùy chọn khác của lệnh polyhedraplot giống như các nội dung của lệnh plot3d , ta cũng có thể gán một giá trị PLOT3D cho một biến, lưu nó vào một tập tin, sau đó truy xuất lại .
b. Ví dụ minh họa .
+Vẽ tứ diện từ điểm gốc O(0,0,0)
with(plots):
> with(plots):
> polyhedraplot([0,0,0],polytype=tetrahedron,style=PATCH, scaling=CONSTRAINED,orientation=[71,66],axes=normal,labels=[x,y,z]);
+Vẽ tứ diện từ điểm gốc O(0,0,0) và M(5,7,8)
>polyhedraplot([[10,8,8],[0,0,0]],polyscale=3,polytype=tetrahedron,scaling=CONSTRAINED,style=PATCH, orientation=[76,40],axes=normal,labels=[x,y,z]);
+Vẽ khối sáu mặt (hình hộp) từ điểm A(0,1,2) và B(1,-1,-2)
>polyhedraplot([[0,1,2],[1,-1,-2]] ,axes=normal ,polytype=hexahedron,style=PATCH, scaling=CONSTRAINED,orientation=[714,66],labels=[x,y,z]);
a. Cấu trúc lệnh .
> plot3d(biểu thức , x=a..b, y=c..d)
plot3d(f, a..b, c..d)
plot3d([biểu thức f,biểu thức g,biểu thức h], s=a..b, t=c..d)
plot3d([f,g,h], a..b, c..d)
Mô tả:
-Tất cả bốn lệnh khác nhau với hàm plot3d trên đây dùng để xác định mặt cong . Những tính năng cho đồ họa đường cong và các đối tượng khác có trong gói plots. Hai lệnh đầu tiên mô tả mặt trong hệ tọa độ Descartes trong khi hai lệnh còn lại mô tả mặt theo tham số.
-Trong lệnh đầu tiên, plot3d (biểu thức1, x = a .. b, y = c .. d), các biểu thức1 theo biến x và y. Khoảng a .. b với a , b là hằng số thực. Khoảng c .. d hoặc là hằng số thực hoặc là biểu thức theo x. Các khoảng nay xác định phạm vi mà biểu thức1 sẽ được vẽ.
- Trong lệnh thứ hai, plot3d (f, a .. b, c .. d), f phải là một thủ tục (procedure) Maple hoặc là phép toán trong đó có hai đối số. Ký hiệu phép toán phải được sử dụng , nghĩa là tên thủ tục được đưa ra mà không có các tham số quy định và khoảng vẽ phải được cho đơn giản dưới dạng a .. b, chứ không phải là một phương trình. Khoảng vẽ c .. d có thể có đối số có giá trị hằng hoặc các thủ tục của một biến thực.
-Một mặt cong tham số có thể được xác định bởi ba biểu thức biểu thức 1, biểu thức 2, biểu thức 3 theo hai biến s, t. Trong lệnh thứ ba, plot3d ([biểu thức 1, biểu thức 2, biểu thức 3], s = a .. b, t = c .. d), các biểu thức này chứa các công thức theo s và t.
- Cuối cùng, trong lệnh thứ tư, plot3d ([f, g, h], a .. b, c .. d), f, g, h phải là các thủ tục Maple hoặc các phép toán theo hai đối số , kèm theo các ký hiệu và công thức toán học . Các khoảng a...b và c..d là các số thực xác định phạm vi vẽ đồ thị .
-Bất kỳ đối số bổ sung nào cũng được hiểu là tùy chọn được quy định như là một phương trình của các hình thức tùy chọn = giá trị. Ví dụ, tùy chọn grid = [m, n] trong đó m và n là các số nguyên dương xác định rằng đồ thị được xây dựng trên một lưới m x n lưới tại các điểm cách đều nhau trong phạm vi a .. b và c .. d tương ứng .
-Theo mặc định lưới 25 x 25 được sử dụng, do đó sẽ có 625 điểm được tạo ra. Các tùy chọn khác bao gồm đặc điểm kỹ thuật của hệ thống trục tọa độ , các style , màu sắc , độ dày , tên trục ...
-Hệ tọa độ mặc định cho tất cả lệnh vẽ 3 chiều trong Maple V là Cartesian . Các tùy chọn coords cho phép người dùng thay đổi hệ tọa độ trong đồ họa bao gồm : bipolarcylindrical (lưỡng trụ cực) , bispherical (lưỡng cầu), cardiodal (tâm) , cardiodcylindrical (trụ tâm), casscylindrical (trụ oval cassini) , confocalellip (elliptic trùng tiêu điểm), confocalparab (parabolic trùng tiêu điểm),conical (nón) , cylindrical (trụ) , ellcylindrical (elliptic trụ ) , ellipsoidal (ellipse tròn xoay) , hypercylindrical (hyperbolic trụ) , invcasscylindrical (trụ oval cassini nghịch), invellcylindrical (trụ elliptic nghịch) , invoblspheroidal (cầu dẹt nghịch) , invprospheroidal (phỏng cầu nghịch) , logcoshcylindrical (trụ loga cos hyperbolic) , logcylindrical (trụ loga) , maxwellcylindrical (trụ maxell) , oblatespheroidal (cầu dẹt), paraboloidal (parabol tròn xoay), paracylindrical (song trụ) , prolatespheroidal (phỏng cầu ), rosecylindrical (trụ hoa) , sixsphere (cầu lục), spherical (cầu) , tangentcylindrical (tiếp trụ) , tangentsphere (tiếp cầu) , và toroidal (xuyến) .
- Các phép biến đổi từ hệ khác về hệ tọa độ Descartes
(u, v, w) --> (x, y, z)
được biểu diễn như sau
bipolarcylindrical: (lưỡng cực trụ - Spiegel )
x = a*sinh(v)/(cosh(v)-cos(u))
y = a*sin(u)/(cosh(v)-cos(u))
z = w
bispherical: (lưỡng cầu)
x = sin(u)*cos(w)/d
y = sin(u)*sin(w)/d
z = sinh(v)/d ( với d = cosh(v) - cos(u) )
cardiodal: (tâm)
x = u*v*cos(w)/(u^2+v^2)^2
y = u*v*sin(w)/(u^2+v^2)^2
z = (u^2-v^2)/2/(u^2+v^2)^2
cardiodcylindrical: (trụ tâm)
x = (u^2-v^2)/2/(u^2+v^2)^2
y = u*v/(u^2+v^2)^2
z = w
casscylindrical: (trụ oval cassini - Cassinian-oval cylinder)
x = a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)+exp(u)*cos(v)+1)^(1/2)
y = a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)-exp(u)*cos(v)-1)^(1/2)
z = w
confocalellip: (elliptic trùng tiêu điểm - confocal elliptic)
x = ((a^2-u)*(a^2-v)*(a^2-w)/(a^2-b^2)/(a^2-c^2))^(1/2)
y = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2)/(b^2-c^2))^(1/2)
z = ((c^2-u)*(c^2-v)*(c^2-w)/(c^2-a^2)/(c^2-b^2))^(1/2)
confocalparab: (parabolic trùng tiêu điểm - confocal parabolic)
x = ((a^2-u)*(a^2-v)*(a^2-w)/(b^2-a^2))^(1/2)
y = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2) )^(1/2)
z = (a^2+b^2-u-v-w)/2
conical: (nón)
x = u*v*w/(a*b)
y = u/b*((v^2 - b^2)*(b^2-w^2)/(a^2-b^2))^(1/2)
z = u/a*((a^2 - v^2)*(a^2 - w^2)/(a^2-b^2))^(1/2)
cylindrical: (trụ)
x = u*cos(y)
y = u*sin(y)
z = w
ellcylindrical: (elliptic trụ - elliptic cylindrical)
x = a*cosh(u)*cos(v)
y = a*sinh(u)*sin(v)
z = w
ellipsoidal: (ellipse tròn xoay)
x = u*v*w/a/b
y = ((u^2-b^2)*(v^2-b^2)*(b^2-w^2)/(a^2-b^2))^(1/2)/b
z = ((u^2-a^2)*(a^2-v^2)*(a^2-w^2)/(a^2-b^2))^(1/2)/a
hypercylindrical: (hyperbolic trụ - hyperbolic cylinder)
x = ((u^2+v^2)^(1/2)+u)^(1/2)
y = ((u^2+v^2)^(1/2)-u)^(1/2)
z = w
invcasscylindrical: (trụ oval cassini nghịch - inverse Cassinian-oval cylinder)
x = a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) +
exp(u)*cos(v)+1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)
y = a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) -
exp(u)*cos(v)-1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)
z = w
invellcylindrical: (trụ elliptic nghịch - inverse elliptic cylinder)
x = a*cosh(u)*cos(v)/(cosh(u)^2-sin(v)^2)
y = a*sinh(u)*sin(v)/(cosh(u)^2-sin(v)^2)
z = w
invoblspheroidal: (cầu dẹt nghịch - inverse oblate spheroidal)
x = a*cosh(u)*sin(v)*cos(w)/(cosh(u)^2-cos(v)^2)
y = a*cosh(u)*sin(v)*sin(w)/(cosh(u)^2-cos(v)^2)
z = a*sinh(u)*cos(v)/(cosh(u)^2-cos(v)^2)
invprospheroidal: (phỏng cầu nghịch - inverse prolate spheroidal)
x = a*sinh(u)*sin(v)*cos(w)/(cosh(u)^2-sin(v)^2)
y = a*sinh(u)*sin(v)*sin(w)/(cosh(u)^2-sin(v)^2)
z = a*cosh(u)*cos(v)/(cosh(u)^2-sin(v)^2)
logcoshcylindrical: (trụ loga cos hyperbolic - ln cosh cylinder)
x = a/Pi*ln(cosh(u)^2-sin(v)^2)
y = 2*a/Pi*arctan(tanh(u)*tan(v))
z = w
maxwellcylindrical: (trụ maxell)
x = a/Pi*(u+1+exp(u)*cos(v))
y = a/Pi*(v+exp(u)*sin(v))
z = w
oblatespheroidal: (cầu dẹt)
x = a*cosh(u)*sin(v)*cos(w)
y = a*cosh(u)*sin(v)*sin(w)
z = a*sinh(u)*cos(v)
paraboloidal: (parabol tròn xoay - Spiegel )
x = u*v*cos(w)
y = u*v*sin(w)
z = (u^2 - v^2)/2
paraboloidal2: (parabol tròn xoay2 - Moon )
x = 2*((u-a)*(a-v)*(a-w)/(a-b))^(1/2)
y = 2*((u-b)*(b-v)*(b-w)/(a-b))^(1/2)
z = u+v+w-a-b
paracylindrical: (song trụ)
x = (u^2 - v^2)/2
y = u*v
z = w
prolatespheroidal: (phỏng cầu )
x = a*sinh(u)*sin(v)*cos(w)
y=a*sinh(u)*sin(v)*sin(w)
z=a*cosh(u)*cos(v)
rectangular: ( vuông góc)
x = u
y = v
z = w
rosecylindrical: (trụ hoa)
x = ((u^2+v^2)^(1/2)+u)^(1/2)/(u^2+v^2)^(1/2)
y = ((u^2+v^2)^(1/2)-u)^(1/2)/(u^2+v^2)^(1/2)
z = w
sixsphere: (cầu lục - 6-sphere)
x = u/(u^2+v^2+w^2)
y = v/(u^2+v^2+w^2)
z = w/(u^2+v^2+w^2)
spherical: (cầu)
x = u*cos(v)*sin(w)
y = u*sin(v)*sin(w)
z = u*cos(w)
tangentcylindrical: (tiếp trụ)
x = u/(u^2+v^2)
y = v/(u^2+v^2)
z = w
tangentsphere: (tiếp cầu)
x = u*cos(w)/(u^2+v^2)
y = u*sin(w)/(u^2+v^2)
z = v/(u^2+v^2)
toroidal: (xuyến)
x = a*sinh(v)*cos(w)/d
y = a*sinh(v)*sin(w)/d
z = a*sin(u)/d ( với d = cosh(v) - cos(u) )
b. Ví dụ minh họa .
+Vẽ mặt cong $z = f(x,y) = x.siny$
> plot3d(x*sin(y),x=-3..3, y=-3..3,axes=frame,style=patch);
+Vẽ mặt cong $z = f(x,y) = (1.3)^x . sin(y)$ trong hệ tọa độ cầu
> plot3d((1.3)^x * sin(y),x=-1..2*Pi,y=0..Pi,coords=spherical,style=patch,axes=frame);
+Vẽ mặt cong $[1,x,y]$ trong hệ tọa độ toroidal
> plot3d([1,x,y],x=0..2*Pi,y=0..2*Pi,coords=toroidal(10),scaling=constrained,style =patch,axes=frame);
2.1.6 Mặt cong trong hệ tọa độ cầu .
-Trong phần kế tiếp chúng ta tìm hiểu về các lệnh đồ họa 3D trong hai hệ tọa độ rất phổ biến là hệ tọa độ cầu $r, \theta, \phi$ và hệ tọa độ trụ $r, \theta, z$ với các thành phần mô tả như ở hình vẽ sau
a. Cấu trúc lệnh .
>sphereplot (L, r1, r2, tùy chọn);
Các tham số:
L - là một thủ tục hoặc biểu thức hai biến số, hoặc một danh sách gồm 3 thủ tục hoặc 3 biểu thức như vậy
r1, r2 - phạm vi khoảng để vẽ với các số thực a .. b
Mô tả
-Hàm sphereplot minh họa một bề mặt ba chiều hoặc mặt tham số trong hệ tọa độ cầu. Các hàm thành phần có thể được biểu diễn theo một trong các dạng của biểu thức hoặc thủ tục. Nếu L không phải là một danh sách, thì L đại diện cho bán kính được cho cùng với theta và phi. Nếu L là một danh sách, thì ba thành phần này đại diện cho bán kính, theta và phi tương ứng.
-Những đối số còn lại được hiểu là các tùy chọn được quy định như phương trình của các hình thức lựa chọn = giá trị. Các tùy chọn này tương tự như trong plot3d . Ví dụ, khi lựa chọn lưới = [m, n] nghĩa là tập hợp các điểm của đồ thị ba chiều cần vẽ được định trên một lưới m x n .
b. Ví dụ minh họa .
+Vẽ mặt cầu $r = 4$ , mặt cong $arccos^2z .sinθ$ , $[zθ,sin(θ/2),zcosθ]$
và mặt cong $(5.cos^y -x)/2 $,
>sphereplot(4,theta=0..2*Pi,phi=0..Pi,axes=frame,style=patch);
> sphereplot(arccos(z)^2* sin(theta),z=-1..2*Pi,theta=0..Pi,style=patch,color=z,axes=frame);
>sphereplot([z*theta,sin(theta/2),z*cos(theta)],theta=0..Pi,z=-2..2);
2.1.7 Mặt cong trong hệ tọa độ trụ .
a. Cấu trúc lệnh .
> cylinderplot (L, r1, r2, tùy chọn);
các tham số:
L - một thủ tục hoặc biểu thức chứa hai biến số, hoặc một danh sách gồm ba thủ tục hoặc ba biểu thức .
r1, r2 - phạm vi của khoảng cần vẽ là các số thực a .. b
Mô tả:
-Hàm cylinderplot dùng cho đồ họa ba chiều của một mặt tổng quát hoặc mặt tham số trong hệ tọa độ trụ. Các hàm thành phần có thể được biểu diễn theo một trong các dạng của biểu thức hoặc thủ tục. Nếu L không phải là một danh sách, thì L đại diện cho bán kính được xác định cùng với các tọa độ theta và z với r1 và r2 là phạm vi khoảng cần vẽ cho 2 tọa độ θ , z . Nếu L là danh sách, thì ba thành phần của L là đại diện tham số của bán kính tọa độ, theta, và z, tương ứng. Trong trường hợp này, r1 và r2 là phạm vi khoảng cần vẽ cho hai tham số của bề mặt.
--Những đối số còn lại được hiểu là các tùy chọn được quy định như phương trình của các hình thức lựa chọn = giá trị. Các tùy chọn này tương tự như trong plot3d . Ví dụ, khi lựa chọn lưới = [m, n] nghĩa là tập hợp các điểm của đồ thị ba chiều cần vẽ được định trên một lưới m x n .
b. Ví dụ minh họa .
+Vẽ mặt trụ $r = 1$ , mặt cong $z^2 + 3cos2θ$ , $[zθ ,θ ,cos(z^2)]$
và mặt cong $(5cos^2y -1)/3$,
with(plots):
> cylinderplot(1,theta=0..2*Pi,z=-1..1,color=z,style = patch,axes=frame);
> cylinderplot(z^2 + 3*cos(2*theta),theta=0..Pi,z=0..3,color=z^2*cos(theta/2),style = patch,axes=frame);
> f := (5*cos(y)^2 -1)/3;
> cylinderplot(f, x=0..2*Pi,y=-Pi..Pi,style=PATCH, color = f,axes=frame);
> cylinderplot([z*theta,theta,cos(z^2)],theta=0..Pi,z=-2..2, color = theta,style = patch,axes=frame);
2.1.8 Mặt cong dạng hàm ẩn .
a. Cấu trúc lệnh .
> implicitplot3d (biểu thức 1, x = a .. b, y = c .. d, z = p .. q, <tùy chọn>)
implicitplot3d (f, a .. b, c .. d, p .. q, <tùy chọn>)
các tham số:
f - phương trình cần vẽ
biểu thức1 - biểu diễn phương trình trong x, y, z
a, b, c, d, p, q - hằng số thực
Mô tả:
-Hàm implicitplot3d dùng để vẽ đồ thị ba chiều của các mặt cong được xác định dưới dạng ẩn . Đặc trưng của hàm này sử dụng một thuật toán dựa trên phép biến đổi số tam giác thành tứ diện kết hợp với phép nội suy đơn giản mà không cần thực hiện các phép tính toán symbolic . Theo mặc định, mặt cong được cho trong hệ tọa độ Descartes .
-Trong lệnh đầu tiên nêu trên, implicitplot3d (biểu thức 1, x = a .. b, y = c .. d, z = p .. q) , các biểu thức 1 dạng phương trình phải có thành phần là những biểu hiện Maple trong tên x, y và z. Tham số biểu thức 1 cũng có thể là một biểu thức Maple thay vì một phương trình - trong trường hợp này, phương trình biều thức 1 = 0 sẽ được vẽ. Phạm vi khoảng cần vẽ x = a .. b, y = c .. d, z = p .. q phải là hằng số thực.
-Trong lệnh thứ hai, implicitplot3d (f, a .. b, c .. d, p .. q,<tùy chọn>) , giả định được đưa ra là các phương trình f chỉ bao gồm các thủ tục Maple hoặc các phép toán thay vì một phương trình - trong trường hợp này, phương trình f = 0 (mặc định) sẽ được vẽ. Ký hiệu phép toán cũng bắt buộc phải sử dụng, ví dụ như tên thủ tục được đưa ra mà không có các thông số được quy định và phạm vi khoảng cần vẽ phải được đơn giản dưới hình thức a .. b, c .. d, p và q .. chứ không phải là một phương trình.
-Bất kỳ đối số bổ sung nào cũng được hiểu là tùy chọn , được quy định như phương trình của các hình thức lựa chọn = giá trị. Ví dụ, lưới tùy chọn = [m, n, r] trong đó m, n và r là số nguyên dương xác định rằng hàm implicitplot3d thực hiện với mặt cong sẽ được xây dựng trên một lưới m x n x r tại các điểm cách đều nhau trong phạm vi khoảng vẽ a .. b, c .. d, p .. q tương ứng . Theo mặc định lưới được sử dụng là 10x10x10 . Các tùy chọn còn lại là tương tự như trong hàm plot3d.
b. Ví dụ minh họa .
+Vẽ mặt trụ $x^3 + y^3 + z^3 + 1 = (x + y + z + 1)^3$ , mặt cong $r = (1.3)^x * sin(y^2)$ , thủ tục
{ p:= proc(x,y,z) if x^2 < y then x^2 + y^2 else x^2 - y^2 +x*y fi end : }
và mặt cong $r^2+z^2+θ^2 - rz = 9$,
with(plots):
> implicitplot3d( x^3 + y^3 + z^3 + 1 = (x + y + z + 1)^3,x=-2..2,y=-2..2,
> z=-2..2,grid=[15,15,15],style=patch,color=sin(x*y),axes=frame);
> implicitplot3d(r = (1.3)^x * sin(y^2),x=-1..2*Pi,y=0..Pi,r=0.1..5,
> coords=spherical,style=patch,color=z,axes=frame);
> p:= proc(x,y,z) if x^2 < y then x^2 + y^2 else x^2 - y^2 +x*y fi end:
> implicitplot3d(p,-2..2,-1..3,0..3,style=patch,color=z,axes=frame);
> implicitplot3d(r^2+z^2+theta^2 - r*z = 9, theta=-Pi..Pi,r=0..3,z=-3..3,
> coords=cylindrical,style=patch,color=cos(r*z*theta),axes=frame);
III . Công thức tính chiều dài cung , độ cong và diện tích - Các bước chuẩn bị cho Maple procedure .
3.1 Chiều dài cung .
Công thức tính toán chiều dài cung .
-Cho đường cong có biểu diễn hiển là hàm số $y=f(x)$ khả vi liên tục trên đoạn $[a,b]$ , chiều dài cung của đường cong từ a đến b là
$L[a,b]= \int_{a}^{b} \sqrt{1+[f '(x)]^2}dx$
-Cho đường cong có phương trình biểu diễn dạng tham số $x=x(t) ; y=y(t)$ trong đó các hàm $x(t) , y(t)$ khả vi liên tục trên đoạn $[p,q]$ , chiều dài cung của đường cong từ $p$ đến $q$ là
$L[p,q] = \int_{p}^{q} \sqrt{[x'(t)]^2+[y '(t)]^2}dt $
-Cho đường cong có phương trình biểu diễn dạng tọa độ cực $r=r(θ)$ với hàm $r(θ)$ khả vi liên tục trên đoạn $[\alpha,\beta]$ , chiều dài cung của đường cong từ $\alpha$ đến $\beta$ là
$L[\alpha,\beta]= \int_{\alpha}^{\beta} \sqrt{[r(\theta)]^2+[r'(\theta)]^2}d \theta$
3.2 Độ cong .
Công thức tính toán độ cong .
-Cho đường cong có biểu diễn hiển là hàm số $y=f(x)$ khả vi liên tục cấp 2 trên đoạn $[a,b]$ , độ cong đại số tại điểm $x \in [a,b]$ là
$C[x]= \frac{y"}{(1+y'^2)^{3/2}}$
-Cho đường cong có phương trình biểu diễn dạng tham số $x=x(t) ; y=y(t)$ trong đó các hàm $x(t) , y(t)$ khả vi liên tục cấp 2 trên đoạn $[p,q]$ , độ cong đại số tại điểm $t \in [p,q]$ là
$C[t]= \frac{x'y"-x"y'}{(x'^2+y'^2)^{3/2}}$
-Cho đường cong có phương trình biểu diễn dạng tọa độ cực $r=r(θ)$ với hàm $r(θ)$ khả vi liên tục cấp 2 trên đoạn $[\alpha,\beta]$ , độ cong đại số tại điểm $θ \in [\alpha,\beta]$ là
$C[\theta]= \frac{r^2+2r'^2-rr"}{(r^2+r'^2)^{3/2}}$
3.3 Diện tích .
Công thức tính toán diện tích giới hạn .
-Cho đường cong có biểu diễn hiển là hàm số $y=f(x)$ liên tục trên đoạn $[a,b]$ , diện tích giới hạn bởi đường cong và $x = a ; x = b$ là
$S= \int_{a}^{b} f(x) dx$
-Cho đường cong có phương trình biểu diễn dạng tham số $x=x(t) ; y=y(t)$ trong đó các hàm $x(t) , y(t)$ liên tục trên đoạn $[p,q]$ , diện tích giới hạn bởi đường cong và $t = a ; t = b$ là
$S= \int_{a}^{b} y(t) x'(t) dt$
-Cho đường cong có phương trình biểu diễn dạng tọa độ cực $r=r(θ)$ với hàm $r(θ)$ liên tục trên đoạn $[\alpha,\beta]$ , diện tích giới hạn bởi đường cong và $t = \alpha ; t = \beta$ là
$S=1/2 \int_{\alpha }^{ \beta} r^2 d \theta$

3.4 Các bước chuẩn bị cho Maple procedure .
Cấu trúc procedure
proc (argseq)
local nseq;
global nseq;
options nseq;
description stringseq;
statseq ;
end :
-Thủ tục là một biểu thức có giá trị có thể được gán cho một tên gọi như một hàm lệnh .
-Các argseq (dãy đối số ) trong ngoặc đơn, có thể là rỗng , xác định tên các tham số chính thức. Mỗi tham số là một tên tiếp theo một loại đặc tả tùy chọn trước bởi một dấu hai chấm . Nếu đặc điểm kỹ thuật của tham số được cung cấp, Maple sẽ tạo ra một lỗi khi đối số của các loại không chính xác được truyền cho hàm . Maple cũng sẽ tạo ra một lỗi nếu thiếu hoặc không có một đối số, nhưng chỉ ở thời điểm đó như một đối số cần thiết cho lần đầu tiên .
-Các cụm từ local nseq ( dãy biến địa phương ) ; local nseq ( dãy biến toàn cục ) ; là những tùy chọn về quy định các biến trong thủ tục . Nếu có, chúng chỉ định, tương ứng, tên của các biến địa phương và toàn cục và các tùy chọn có hiệu lực . Biến địa phương chỉ ghi nhận và truy xuất các thông tin trong thủ tục . Biến toàn cục lưu trữ , truy xuất trong toàn worksheet .
-Các stringseq ( dãy chuỗi ) mô tả; phần quy định cụ thể một hoặc nhiều dòng mô tả về các thủ tục. Khi thủ tục được in ra , thông tin mô tả này cũng được in kèm theo .
Một cách tóm tắt ta có thể hiểu cấu trúc của một procedure như sau :
> tên gọi thủ tục := proc(tên các đối số - hoặc rỗng)
> local tên các biến địa phương ; global tên các biến toàn cục ;
> with(tên các package cần truy xuất ) :
> các lệnh thực hiện - vòng lặp - điều kiện ;
> end :
-
IV . Lời kết .
Đến đây chúng ta kết thúc phần nghiên cứu những tính chất cơ bản của các đường cong từ Pe đến Sp (43-53) cùng với việc khảo sát các tính toán những đặc trưng chi tiết của chúng . Điểm đáng lưu ý trong bài viết này là phần minh họa đồ thị bằng các trình ứng dụng GP , MapleV và các công cụ trực tuyến DESMOS , SMS - sử dụng SMS tìm chiều dài cung và diện tích giới hạn của đường cong trên một đoạn cho trước . Phần II của bài viết tác giả cũng tiếp tục trình bày về các lệnh của trình Maple về đồ họa 3D cho các hình đa diện , các mặt cong và các lệnh mở đầu cho một procedure trong Maple.
Trong bài viết sau chúng ta sẽ tiếp tục khảo sát các đường cong từ Sp đến Wi (54-64) , vẽ đồ thị bằng các công cụ trực tuyến hoặc trình ứng dụng , và tìm hiểu thêm về các procedure viết bằng trình Maple V phục vụ cho việc tính toán .
Cám ơn các bạn đã đọc bài viết này , hẹn gặp lại .
Trần hồng Cơ
Ngày 10 / 06/ 2014 .
-------------------------------------------------------------------------------------------
Khoa học là một điều tuyệt vời khi không phải dùng nó để kiếm sống.
Albert Einstein .













.gif)








































































.gif)







































































