Một số phần mềm ứng dụng .
Phần 2 .Nguồn tham khảo : http://xahoithongtin.com.vn
Những ứng dụng tốt nhất dành cho giáo dục
18:29, Chủ Nhật, 06/03/2016 (GMT+7)
Các thiết bị điện thoại thông minh
và máy tính bảng đã thay đổi cuộc sống của chúng ta. Chúng không chỉ là
một phương tiện hiệu quả để giao tiếp mà còn giúp chúng ta học tập và
khám phá thế giới. Giờ đây, nếu bạn muốn học một ngôn ngữ mới hoặc thậm
chí học vật lý, tất cả đều trong tầm tay bạn. Bài viết này sẽ giới thiệu
danh sách 10 ứng dụng Android thuộc lĩnh vực giáo dục tốt nhất cho cả
trẻ em và người lớn.
1. Duolingo
Học một ngôn ngữ mới chưa bao giờ được dễ dàng hơn, nhưng chúng ta hãy đối mặt với nó: với tất cả các sản phẩm và phần mềm có sẵn. Giá của nó có thể khá cao với một số người nhưng ứng dụng Duolingo cũng có hỗ trợ học một số ngôn ngữ mới, miễn phí! Mặc dù phần được miễn phí này chắc chắn không đủ để đáp ứng đa số người dùng. Với Duolingo, bạn có thể đặt ra mục tiêu cụ thể cho bản thân sẽ sử dụng ứng dụng hàng ngày như thế nào. Không chỉ dễ sử dụng, thiết kế đầy màu sắc và hấp dẫn, các bài học còn khá ngắn gọn sẽ giữ cho bạn hứng thú quay trở lại tiếp tục khám phá ứng dụng.
2. Endless Alphabet
Endless Alphabet, một ứng dụng giáo dục dành cho trẻ em có thể sẽ góp phần cách mạng hóa cách trẻ học. Ứng dụng này đã đưa ra những bảng chữ cái và biến nó thành một trò chơi phong phú của chữ cái ngớ ngẩn. Không chỉ có trẻ em sẽ trở nên quen thuộc với các chữ cái và âm thanh của chúng mà các em còn được giới thiệu từ mới, và ý nghĩa của những từ thông qua những mẫu chuyện vui ngắn.
3. Khan Academy
Nếu bạn không tự tin 100% về kỹ năng học tập của mình (cho dù bạn đang ở lứa tuổi 5 hay 85), Khan Academy sẽ hướng dẫn bạn qua các bước rất đơn giản để giải quyết hầu như bất kỳ vấn đề nào bạn có thể gặp phải. Trong khi danh mục lớn nhất của Học viện Khan là toán học, cung cấp tất cả các bài học từ đơn giản để dạy kèm trẻ trong tất cả mọi thứ từ 1 + 1 đến Lượng giác hay Tích phân. Ứng dụng cũng cung cấp một loạt các bài học "dạy kèm" trong các môn học khác như Vật lý, Lập trình máy tính, lịch sử thế giới…. Nếu bạn là một sinh viên học bất cứ ngành nào thì đây cũng là một ứng dụng bạn không nên bỏ qua.
4. DragonBox Algebra 12 +
DragonBox Algebra 12 + là một ứng dụng được thiết kế cho lứa tuổi từ 12 trở lên. Đây là một ứng dụng tuyệt vời mà sẽ làm tăng sự quen thuộc với các phương trình đại số với hàng trăm câu đố và nhiều bài tập khác nhau học tập chia thành các thuật ngữ đơn giản, bạn sẽ cảm thấy hứng thú không muốn dừng chơi ! Điểm hay nhất của ứng dụng đó là nội dung đã được tối thiểu, tập trung vào việc cho phép các sinh viên tìm hiểu và khám phá các nhiệm vụ, giúp họ thoải mái hơn để tạm dừng bài học và quay trở lại vào bất cứ lúc nào.
5. PBS Kids (Super Why)
Còn cách nào tốt hơn để giáo dục trẻ em hơn là thông qua các nhân vật truyền hình yêu thích của chúng? Trong Super Why! từ ứng dụng PBS Kids, trẻ em sẽ được học về vần và chính tả bằng cách tương tác với siêu sao và tất cả bạn bè của mình. Đây là một dạng hiếm của giáo dục mà trẻ em sẽ rất thích. Ứng dụng được coi là hoàn hảo cho trẻ em lứa tuổi 3-6
6. Pocket Physics (Vật lý bỏ túi)
Các ứng dụng Pocket Physics là ứng dụng hoàn hảo cho bất cứ ai có nhu cầu thông tin liên quan đến vật lý. Bất cứ kiến thức gì bạn muốn biết đều có bên trong ứng dụng nhỏ gọn này và có thể tìm kiếm một cách thuận tiện. Ứng dụng hướng dẫn cho bài tập về nhà một cách sư phạm và có thể giúp bạn nghiên cứu, giải thích rõ các quy trình nguyên tử, chuyển động, đo từ, công thức… một cách rõ ràng. Bạn có thể tìm định nghĩa và câu trả lời một cách nhanh chóng và hiệu quả với ứng dụng nhỏ tiện dụng này.
7. Bản đồ bầu trời (Sky Map)
Với công nghệ la bàn cho bạn biết chính xác những gì chòm sao và các hành tinh bạn sẽ có một bản đồ bầu trời và như đang đứng ở một đài quan sát ảo khi trải nghiệm ứng dụng. Bản cập nhật gần đây đã sửa chữa các lỗi nhỏ, lỗi chính tả, và các vấn đề vị trí, Ứng dụng đã có một thời gian gián đoạn khá dài không có bất kỳ bổ sung cập nhật nào, tuy nhiên gần đây, việc này đã được khởi động lại.
8. Number Endless
Nếu con của bạn không hứng thú với môn Đại số một chút nào, đừng sợ! Ứng dụng Number Endless được tạo ra bởi cùng một nhà phát triển với Endless Alphabet, và dĩ nhiên rất biết cách cuốn hút trẻ em! Các em bé sẽ có cơ hội để nhảy vào các bánh xe đu quay số và khám phá con số cũng như các phương trình toán học cơ bản. Trẻ em sẽ nắm bắt được những khái niệm về những con số thông qua các thiết kế thú vị của trò chơi.
9. Cat in the Hat
Cat in the Hat là một ứng dụng cổ điển cho trẻ em từ 3 tuổi trở lên. Ứng dụng cung cấp những câu chuyện khác nhau với những tương tác và tuỳ chọn đọc thú vị cho người dùng. Bất kỳ lúc nào trong câu chuyện, bạn chạm vào các phần khác nhau của trang để nghe, và đọc mô tả tương ứng.
10. Pocket Code: Giúp tìm hiểu Lập trình
Đây là ứng dụng tuyệt vời cho những ai muốn đặt những bước đi đầu tiên vào lĩnh vực lập trình. Các nhà phát triển đang cố gắng trang bị cho người dùng không chỉ cơ hội học lập trình mà còn là tạo ra chương trình. Nếu bạn không hoàn toàn chắc chắn nên bắt đầu từ đâu, chỉ cần tải về các ứng dụng và đi đến phần "trợ giúp", nơi bạn sẽ tìm thấy hướng dẫn của các loại khác nhau để giúp bạn bắt đầu đi đúng hướng.
Thực tế trên thị trường còn nhiều ứng
dụng dành cho giáo dục thú vị khác nữa như Monkey Junior, Drawing Carl,
Ask me Color & Shape, Duckie Deck… nhưng 10 ứng dụng liệt kê ở trên
bao phủ trên các lĩnh vực khác nhau một cách tổng quát. Còn bạn, nếu
thấy ứng dụng giáo dục nào hay có thể chia sẻ với chúng tôi ở phía dưới
bài viết.
Hải An (Theo TalkAndroid)
Học một ngôn ngữ mới chưa bao giờ được dễ dàng hơn, nhưng chúng ta hãy đối mặt với nó: với tất cả các sản phẩm và phần mềm có sẵn. Giá của nó có thể khá cao với một số người nhưng ứng dụng Duolingo cũng có hỗ trợ học một số ngôn ngữ mới, miễn phí! Mặc dù phần được miễn phí này chắc chắn không đủ để đáp ứng đa số người dùng. Với Duolingo, bạn có thể đặt ra mục tiêu cụ thể cho bản thân sẽ sử dụng ứng dụng hàng ngày như thế nào. Không chỉ dễ sử dụng, thiết kế đầy màu sắc và hấp dẫn, các bài học còn khá ngắn gọn sẽ giữ cho bạn hứng thú quay trở lại tiếp tục khám phá ứng dụng.
Endless Alphabet, một ứng dụng giáo dục dành cho trẻ em có thể sẽ góp phần cách mạng hóa cách trẻ học. Ứng dụng này đã đưa ra những bảng chữ cái và biến nó thành một trò chơi phong phú của chữ cái ngớ ngẩn. Không chỉ có trẻ em sẽ trở nên quen thuộc với các chữ cái và âm thanh của chúng mà các em còn được giới thiệu từ mới, và ý nghĩa của những từ thông qua những mẫu chuyện vui ngắn.
Nếu bạn không tự tin 100% về kỹ năng học tập của mình (cho dù bạn đang ở lứa tuổi 5 hay 85), Khan Academy sẽ hướng dẫn bạn qua các bước rất đơn giản để giải quyết hầu như bất kỳ vấn đề nào bạn có thể gặp phải. Trong khi danh mục lớn nhất của Học viện Khan là toán học, cung cấp tất cả các bài học từ đơn giản để dạy kèm trẻ trong tất cả mọi thứ từ 1 + 1 đến Lượng giác hay Tích phân. Ứng dụng cũng cung cấp một loạt các bài học "dạy kèm" trong các môn học khác như Vật lý, Lập trình máy tính, lịch sử thế giới…. Nếu bạn là một sinh viên học bất cứ ngành nào thì đây cũng là một ứng dụng bạn không nên bỏ qua.
DragonBox Algebra 12 + là một ứng dụng được thiết kế cho lứa tuổi từ 12 trở lên. Đây là một ứng dụng tuyệt vời mà sẽ làm tăng sự quen thuộc với các phương trình đại số với hàng trăm câu đố và nhiều bài tập khác nhau học tập chia thành các thuật ngữ đơn giản, bạn sẽ cảm thấy hứng thú không muốn dừng chơi ! Điểm hay nhất của ứng dụng đó là nội dung đã được tối thiểu, tập trung vào việc cho phép các sinh viên tìm hiểu và khám phá các nhiệm vụ, giúp họ thoải mái hơn để tạm dừng bài học và quay trở lại vào bất cứ lúc nào.
Còn cách nào tốt hơn để giáo dục trẻ em hơn là thông qua các nhân vật truyền hình yêu thích của chúng? Trong Super Why! từ ứng dụng PBS Kids, trẻ em sẽ được học về vần và chính tả bằng cách tương tác với siêu sao và tất cả bạn bè của mình. Đây là một dạng hiếm của giáo dục mà trẻ em sẽ rất thích. Ứng dụng được coi là hoàn hảo cho trẻ em lứa tuổi 3-6
Các ứng dụng Pocket Physics là ứng dụng hoàn hảo cho bất cứ ai có nhu cầu thông tin liên quan đến vật lý. Bất cứ kiến thức gì bạn muốn biết đều có bên trong ứng dụng nhỏ gọn này và có thể tìm kiếm một cách thuận tiện. Ứng dụng hướng dẫn cho bài tập về nhà một cách sư phạm và có thể giúp bạn nghiên cứu, giải thích rõ các quy trình nguyên tử, chuyển động, đo từ, công thức… một cách rõ ràng. Bạn có thể tìm định nghĩa và câu trả lời một cách nhanh chóng và hiệu quả với ứng dụng nhỏ tiện dụng này.
Với công nghệ la bàn cho bạn biết chính xác những gì chòm sao và các hành tinh bạn sẽ có một bản đồ bầu trời và như đang đứng ở một đài quan sát ảo khi trải nghiệm ứng dụng. Bản cập nhật gần đây đã sửa chữa các lỗi nhỏ, lỗi chính tả, và các vấn đề vị trí, Ứng dụng đã có một thời gian gián đoạn khá dài không có bất kỳ bổ sung cập nhật nào, tuy nhiên gần đây, việc này đã được khởi động lại.
Nếu con của bạn không hứng thú với môn Đại số một chút nào, đừng sợ! Ứng dụng Number Endless được tạo ra bởi cùng một nhà phát triển với Endless Alphabet, và dĩ nhiên rất biết cách cuốn hút trẻ em! Các em bé sẽ có cơ hội để nhảy vào các bánh xe đu quay số và khám phá con số cũng như các phương trình toán học cơ bản. Trẻ em sẽ nắm bắt được những khái niệm về những con số thông qua các thiết kế thú vị của trò chơi.
Cat in the Hat là một ứng dụng cổ điển cho trẻ em từ 3 tuổi trở lên. Ứng dụng cung cấp những câu chuyện khác nhau với những tương tác và tuỳ chọn đọc thú vị cho người dùng. Bất kỳ lúc nào trong câu chuyện, bạn chạm vào các phần khác nhau của trang để nghe, và đọc mô tả tương ứng.
Đây là ứng dụng tuyệt vời cho những ai muốn đặt những bước đi đầu tiên vào lĩnh vực lập trình. Các nhà phát triển đang cố gắng trang bị cho người dùng không chỉ cơ hội học lập trình mà còn là tạo ra chương trình. Nếu bạn không hoàn toàn chắc chắn nên bắt đầu từ đâu, chỉ cần tải về các ứng dụng và đi đến phần "trợ giúp", nơi bạn sẽ tìm thấy hướng dẫn của các loại khác nhau để giúp bạn bắt đầu đi đúng hướng.
Hải An (Theo TalkAndroid)
Những ứng dụng đám mây tốt nhất hiện nay để sao lưu dữ liệu
Tầm
quan trọng của thẻ SD và bộ nhớ trong của thiết bị đang giảm dần khi
xuất hiện ngày càng nhiều các dịch vụ lưu trữ đám mây cung cấp những tùy
chọn đa dạng, tiện dụng cho người dùng. Lưu trữ đám mây cho phép bạn
upload và sao lưu dữ liệu trên thiết bị của bạn một nguồn trực tuyến,
giúp bạn tiết kiệm những Gigabyte quý giá của không gian lưu trữ trên
điện thoại hoặc máy tính bảng của bạn.
Amazon Cloud Drive: Tốt nhất cho việc lưu trữ không giới hạn
Dịch
vụ Amazon Cloud Drive có ưu thế nổi trội đó là: Không giới hạn lưu trữ
hình ảnh cũng như tất cả mọi thứ. Không giới hạn về lưu trữ hình ảnh
được áp dụng miễn phí với người dùng sở hữu tài khoản Amazon Prime, hoặc
bạn cần trả 11,99 USD/năm để mua nó độc lập.
Mức
giá này là khá hợp lý vì dịch vụ cho phép bạn tải ảnh không giới hạn,
cộng với bạn có được thêm 5 GB lưu trữ cho video và các tập tin khác.
Vấn đề là, nó không chút để tự tách biệt với hình ảnh dịch vụ Google
Drive / Google miễn phí.
Ngoài
ra, với mức giá 60 USD/năm để người dùng có thể lưu trữ không giới hạn
tất cả mọi thứ trên Amazon Cloud Drive có vẻ là mức giá hấp dẫn nếu so
sánh với 120 USD/năm cho 1 TB của Google Drive và 100 USD/năm/1TB của
Dropbox.
| Không giới hạn lưu trữ tất cả mọi thứ là một điểm ấn tượng trong dịch vụ lưu trữ đám mây của Amazon. |
OneDrive: Tốt nhất cho người dùng yêu thích Microsoft
OneDrive
là một giải pháp lưu trữ trực tuyến miễn phí được cung cấp bởi
Microsoft. Như vậy, OneDrive là tiền đề để sử dụng với các sản phẩm của
Microsoft như Word, Excel và PowerPoint. Nó có tính năng tự động sao lưu
hình ảnh và video, cũng như chia sẻ và kết hợp các tính năng đơn giản.
Ngoài ra, OneDrive tích hợp với Android Wear, nhờ đó bạn có thể xem hình
ảnh của bạn trên màn hình của SmartWatch.
Ứng
dụng này là miễn phí và dễ sử dụng, nếu bạn thường xuyên sử dụng các
tập tin của Microsoft, bạn nên trải nghiệm qua với OneDrive.
Google Drive: Tốt nhất cho những người dùng về cơ bản
Google
Drive là cái tên khó có thể bỏ qua trong danh sách bởi nó cung cấp tới
15 GB lưu trữ miễn phí và hiếm khi gặp lỗi. Google Drive cho thấy mọi
thay đổi của bạn trong tài liệu, cung cấp tùy chọn để cho phép những
người khác xem và chỉnh sửa công việc của bạn, hỗ trợ nhiều loại tập tin
khác nhau.
Đây
là một giải pháp rõ ràng rất tiện cho bất cứ ai sở hữu một tài khoản
Google bởi sự đồng bộ trong hệ sinh thái các dịch vụ và ứng dụng của
Google. Nếu bạn thường xuyên sử dụng Gmail hay Google Search thì Google
Drive cũng trở thành như môi trường sống tự nhiên của bạn.
Google
Drive cũng tích hợp với Google Photos, để cung cấp cho bạn khả năng lưu
trữ ảnh miễn phí không giới hạn, miễn là bức ảnh đảm bảo trong một giới
hạn kích thước tập tin nhất định (điều này Google được đánh giá là khá
hào phóng).
Dropbox: Dịch vụ lưu trữ đám mây được yêu thích nhất trong nhiều năm
Dropbox
có khả năng lưu trữ tương đối nhỏ – chỉ có 2 GB để bắt đầu với - nhưng
người dùng có thể mở rộng lên đến 16 GB bằng nhiều cách khác nhau khá
đơn giản.
Dropbox
vận hành nhanh chóng, trực quan và linh hoạt, các tính năng sao lưu một
cách tự động không phô trương, khá hoàn hảo cho những người dùng muốn
thâm nhập nhanh chóng và xem sự đồng bộ trên máy tính để bàn cũng như
các thiết bị di động trong nháy mắt. Nhìn một cách tổng thể thì Dropbox
khá tuyệt vời một khi bạn đầu tư một chút thời gian mở rộng khả năng lưu
trữ ban đầu.
| Dropbox có dung lượng lưu trữ nhỏ, nhưng ứng dụng được yêu thích vì nó quá dễ dùng và tiện lợi. |
Box: Dịch vụ đơn giản nhất
Box
là ứng dụng miễn phí và rất dễ sử dụng, nó cung cấp 10 GB không gian
lưu trữ miễn phí với một giới hạn tải lên 250 MB. Ngoài ra, bạn được yêu
cầu phải trả 10 USD/năm cho 25 GB dung lượng lưu trữ đám mây bổ sung.
Box
là ứng dụng cơ bản nhất trong danh sách này bởi nó không có tính năng
đặc biệt: nó không chỉ đơn giản để tải lên, tải về và chia sẻ tập tin,
mặc dù nó có thể chỉnh sửa và nhận xét về các tập tin trong các đám mây.
Box cũng có một widget hỗ trợ thông báo cho bạn về bất kỳ thay đổi nào
trong các tài liệu chia sẻ.
| Box là một giải pháp lưu trữ đám mây đơn giản và hiệu quả. |
MediaFire: Tốt nhất cho các tập tin nhỏ
MediaFire
cung cấp lên đến 50 GB không gian lưu trữ miễn phí, dịch vụ này khá
hoàn hảo để lưu hoặc chia sẻ file nhạc hoặc video. Nhưng bạn chỉ nhận
được 12 GB để bắt đầu và phải kiếm phần còn lại, qua giới thiệu người
dùng mới (hoặc bạn cần trả 2,5 USD/tháng cho 100 GB dung lượng lưu trữ
bổ sung).
Mediafire
có đầy đủ các chức năng cơ bản để tải về hình ảnh, tải về và chia sẻ
tài liệu lưu trữ giúp bạn tiết kiệm rất nhiều thời gian.
Bạn
sẽ bị giới hạn 200 MB dung lượng tập tin tải lên trong phiên bản miễn
phí, nhưng nếu cập nhật nhanh chóng cho các tập tin nhỏ là những gì bạn
cần thì nó quá tiện khi yêu cầu này được đáp ứng miễn phí.
| MediaFire cung cấp 12 GB dung lượng lưu trữ cho người dùng miễn phí, nhưng bạn có thể mở rộng lên đến 50 GB miễn phí bằng nhiều cách khác nhau. |
Mega
Mega
cung cấp 50 GB dung lượng lưu trữ miễn phí, làm cho nó một trong những
ứng dụng lưu trữ đám mây miễn phí tốt nhất hiện nay. Tất cả mọi thứ bạn
tải lên sẽ được mã hóa và các khóa mã hóa người dùng có thể tùy biến, vì
vậy bạn sẽ không phải lo ngại về quyền riêng tư. Bạn thậm chí có thể
đồng bộ máy ảnh của bạn trực tiếp vào tài khoản Mega một cách tự động và
sẽ có được một bản sao của hình ảnh và video khi bạn kết nối nó.
| Mega cung cấp một cảnh quan tuyệt đẹp 50 GB dung lượng lưu trữ cho người dùng mới, hoàn toàn miễn phí. |
Hải An (Theo AndroidPIT)
3 công cụ quản lý tất cả các dịch vụ lưu trữ đám mây từ một nơi
Mặc dù không gian miễn phí được cung cấp cho
người sử dụng từ các dịch vụ lưu trữ đám mây như hiện nay là tương đối
lớn, thế nhưng nhiều người vẫn cảm thấy bấy nhiêu đó là chưa đủ. Họ muốn
có nhiều không gian hơn nữa để đáp ứng nhu cầu công việc của mình nhưng
lại chẳng muốn chi tiền cho việc nâng cấp tài khoản, chính vì thế lựa
chọn giải pháp đăng kí nhiều tài khoản trên nhiều dịch vụ lưu trữ đám
mây là thực trạng phổ biến nhất hiện nay. Tuy đây là giải pháp tuyệt vời
nhưng bạn sẽ gặp phải một vài khó khăn, bất tiện khi cần di chuyển các
tập tin từ nơi lưu trữ này đến nơi lưu trữ khác, cũng như sẽ không dễ
dàng cho việc tìm kiếm những tập tin mà bạn đã tải lên. Hơn nữa, việc
truy cập cùng lúc các dịch vụ này sẽ trải qua nhiều bước rườm rà, mất
thời gian.
Nếu
bạn muốn khắc phục những nhược điểm trên, dưới đây là 3 dịch vụ miễn
phí hữu ích dành cho bạn, nó cho phép bạn có thể dễ dàng quản lý tất cả
các tài khoản đám mây của mình và truy cập vào tất cả các tập tin từ một
nơi duy nhất.
Joukuu
là một chương trình miễn phí dành cho hệ điều hành Windows cho phép
người dùng quản lý tất cả các tập tin trên Dropbox, Google Docs, và
Box.net từ máy tính để bàn của họ mà không cần phải chuyển đổi giữa các
cửa sổ riêng biệt. Đơn giản chỉ cần thêm tất cả các tài khoản của bạn
vào chương trình, nó hỗ trợ kéo và thả các tập tin giữa các tài khoản,
hoặc kéo và thả các tập tin từ Windows Explorer vào cửa sổ của Joukuu để
tải lên. Hơn nữa, bạn có thể tải về, mở và chỉnh sửa tài liệu từ máy
tính của bạn hoặc xem tất cả các tập tin từ tất cả các tài khoản cùng
một lúc. Các tập tin được tự động sắp xếp theo các thể loại như tài
liệu, hình ảnh, video và phần còn lại sẽ được đưa vào thể loại khác.
Phiên
bản Lite của Joukuu cho phép bạn thêm một tài khoản cho mỗi dịch vụ đám
mây, bạn sẽ cần phải đăng ký với 60 USD một năm nếu bạn muốn thêm nhiều
hơn một tài khoản Google, Box và Dropbox. Joukuu chỉ hỗ trợ các dịch vụ
Skydrive, SugarSync, Huddle và Zoho sẽ sớm được thêm vào.
Otixo cho phép bạn kết nối với Dropbox, Box, SkyDrive, Google Docs, SugarSync, Picasa, MobileMe, Amazon S3, cũng như các trang
web
FTP và WebDav. Ngoài FTP và WebDAV ra, dịch vụ mở ra rất nhiều cơ hội
như khả năng để thêm 4shared, GoDaddy Online Storage và hàng chục dịch
vụ bất kỳ khác hỗ trợ hai giao thức này.
Không
giống Joukuu, Otixo là một ứng dụng web có nghĩa là bạn phải quản lý
tất cả mọi thứ từ trình duyệt web của mình. May mắn thay, giao diện của
dịch vụ là rất thân thiện với người sử dụng, một khi bạn kết nối với tài
khoản của mình, một hàng các biểu tượng xuất hiện ở trên cùng của màn
hình, mỗi một biểu tượng được gán một nhiệm vụ cụ thể như dán, sao chép,
tải, chia sẻ, ... Để tải lên các tập tin bạn có thể kéo và thả chúng
vào trong cửa sổ trình duyệt, thậm chí bạn có thể sao chép hoặc di
chuyển các tập tin từ một trong những dịch vụ khác mà không cần tải về
máy tính của bạn. Một tính năng tuyệt vời nữa của Otixo là khả năng lập
bản đồ các dữ liệu từ tài khoản Otixo của bạn như một WebDAV trên
Windows Explorer. Bằng cách này bạn có thể truy cập vào tất cả các đám
mây của bạn ngay từ Windows Explorer trên máy tính. Lưu ý rằng: dịch vụ
chỉ cung cấp 250 MB băng thông hàng tháng trên tài khoản miễn phí cá
nhân. Tài khoản kinh doanh sẽ không có giới hạn nhưng bạn sẽ phải trả
phí 10 USD/tháng.
Primadesk
là một ứng dụng web hỗ trợ trên 30 dịch vụ, bao gồm cả Box.net,
Dropbox, Facebook, Gmail, Google Docs, SkyDrive, Picasa, Hotmail,
Photobucket, Shutterfly, Smugmug, Snapfish, SugarSync, Flickr, Yahoo
Mail, Evernote và Zoho. Sau khi kết nối tài khoản của bạn vào Primadesk,
bạn có thể xem tất cả các tài liệu của bạn ở một nơi, các tập tin có
thể được tìm thấy trên tất cả các dịch vụ được sắp xếp theo ngày, chủ đề
và nội dung, sao chép và dán các tập tin hoặc kéo và thả giữa các dịch
vụ
Primadesk
cũng hỗ trợ IMAP để bạn có thể mang chúng về hộp thư của mình. Đối với
tài khoản miễn phí bạn sẽ có được 1GB lưu trữ từ Primadesk nhưng bạn chỉ
có thể kết nối đến 5 dịch vụ.
Châu Quốc Hùng
Thay đổi địa chỉ IP bằng một cú nhấn chuột
Khi lướt web trên internet, địa chỉ IP là thành phần duy nhất
có thể xác định danh tính của bạn, bao gồm các thông tin nhạy cảm hoặc
vị trí địa lý. Chính vì điều đó, một số trang web dịch vụ có thể chặn
bất kỳ IP đến từ bất cứ quốc gia nào mà họ không muốn chia sẻ dữ liệu.
Tuy nhiên, nếu bạn sử dụng một ứng dụng mạng riêng ảo (VPN), bạn có thể
bỏ qua rào cản này và xem nội dung hoặc truy cập vào tên miền bị chặn dễ
dàng. Mặc dù đây là cách khá tốt, thế nhưng bạn sẽ dễ bị các cuộc tấn
công của tin tặc và mã độc hại, nếu họ biết địa chỉ IP thực và tìm thấy
bất kỳ lỗ hổng bảo mật trên máy tính của bạn.
X-Proxy
là ứng dụng cho phép bạn lướt web nặc danh, truy cập nội dung bị chặn
và ngăn chặn các cuộc tấn công từ tin tặc. Ứng dụng này có giao diện rất
đơn giản với các thẻ Home, Proxy List và Settings được đặt ở phía trên.
Sau ba thẻ này, bạn có thể nhìn thấy dữ liệu về địa chỉ IP thực (Real
IP), IP giả (Fake IP) và chế độ ẩn danh (Anonym). Bây giờ, bạn hãy nhấn
vào thẻ Proxy List để có được một danh sách các máy chủ proxy nhằm lựa
chọn cho việc ẩn danh.
Tiếp
đến, bạn nhấp đúp chuột vào bất kỳ một proxy giả có sẵn trong danh sách
thay đổi địa chỉ IP của bạn, khi đó một thông báo ở góc dưới bên phải
của màn hình sẽ xuất hiện đảm bảo chắc chắn rằng bạn đã thay đổi địa chỉ
IP.
Thẻ
Settings trong giao diện chính cho phép bạn thay đổi ngôn ngữ, giao
diện của chương trình, xem thông tin giấu tên, kiểm tra tốc độ
internet…Để quay trở lại địa chỉ IP thực của bạn, bạn chỉ cần nhấn chọn
tùy chọn Restore Real IP trong danh sách.
Lưu
ý, khi sử dụng công cụ này, khi duyệt web bạn sẽ nhận được một chút
chậm trễ sau khi thay đổi IP. X-Proxy hoạt động trên cả hai phiên bản
32-bit và 64-bit của Windows XP, Windows Vista, Windows 7 và Windows 8
và yêu cầu máy bạn phải cài Microsoft .NET Framework 4 Client Profile
(x86 and x64).
Tải X-Proxy tại địa chỉ http://www.saucessoftware.com/index.php/proyectos/x-proxy
Châu Quốc Hùng
Chuyển đổi qua lại các tập tin giữa Dropbox, Google Drive và SkyDrive
10:19, Thứ Sáu, 18/05/2012 (GMT+7)
Với giải pháp sao lưu trực tuyến bằng các dịch vụ lưu trữ đám
mây phổ biến hiện nay như: Dropbox, Google Drive, SkyDrive bạn có thể
khôi phục, sử dụng dữ liệu của mình bất cứ lúc nào mình mong muốn. Tuy
nhiên để đảm bảo việc đồng bộ, sao lưu đạt hiệu quả cao nhất, một số
người dùng thường đăng kí tài khoản trên nhiều dịch vụ khác nhau. Nếu
bạn là một trong số những người đó và đang tìm cách để chuyển đổi qua
lại các tập tin sử dụng cho mục đích của riêng mình thì trong trường hợp
này dịch vụ trực SMEStorage sẽ hữu ích đối với bạn
SMEStorage
là dịch vụ trực tuyến cho phép bạn truy cập và quản lý nhiều tài khoản
lưu trữ đám mây từ một nơi duy nhất, do đó khi bạn cần chuyển đổi các
tập tin từ dịch vụ này đến dịch vụ khác bạn có thể làm điều đó dễ dàng
mà không cần phải thực hiện các bước tải lên, tải xuống vừa ngốn băng
thông, vừa mất thời gian. Để khai thác sử dụng dịch vụ này bạn có thể
làm theo các hướng dẫn dưới đây.
Đăng kí sử dụng
Bước 1 : Truy cập địa chỉ http://www.smestorage.com/ sau
đó tạo một tài khoản miễn phí từ trang này. Lúc này bạn sẽ được hỗ trợ 5
GB Amazon S3 bởi SMEStorage cộng với 3 dịch vụ lưu trữ đám mây bất kỳ
mà bạn có thể quản lý các tài khoản đó.
Bước
2: Khi bạn tạo và xác nhận tài khoản của bạn, đăng nhập vào bảng quản
trị của mình. Tại đây, bạn chọn tùy chọn Manage Cloud Providers để bắt
đầu.
Bước
3: Bây giờ, trong phần Providers currently in use, bạn nhấn vào nút Add
new provider để thêm Dropbox, Google Docs (cũng như Google Drive) và
SkyDrive.
Bước
4: Bạn cần xác thực tài khoản của bạn và cung cấp truy cập dịch vụ lưu
trữ đám mây SMEStorage cho họ bằng cách cấp một số điều khoản trong tài
khoản của bạn. Sau khi thực hiện, SMEStorage sẽ đồng bộ hóa tất cả các
file của bạn để bạn có thể truy cập tất cả các dịch vụ thông qua
SMEStorage.
Cuối cùng, một khi đã thêm tất cả các tài khoản, bạn có thể bắt đầu chuyển đổi tập tin giữa các dịch vụ với nhau.
Di chuyển các tập tin
Bước
1: Mở trang quản lý tập tin của SMEStorage ( không phải trong phiên
bản beta) và mở tài khoản lưu trữ đám mây mà bạn muốn sao chép các tập
tin của bạn.
Bước
2: Bây giờ, bạn tạo ra một liên kết tải về một tập tin từ một trong
những dịch vụ lưu trữ đám mây và sau đó sử dụng tính năng tải lên từ xa
trên cùng một liên kết để tải nó lên các dịch vụ khác. Vì vậy, việc mà
bạn cần làm là điều hướng đến các tập tin bạn muốn di chuyển đến một tài
khoản đám mây, sau đó nhấp chuột vào nó và chọn tùy chọn Generate
direct link rồi sao chép vào clipboard của bạn.
Bước
3: Mở tài khoản đích và điều hướng đến thư mục mà bạn muốn sao chép các
tập tin của bạn. Nhấp vào nút tải về (Download) và dán liên kết tải về
trực tiếp mà bạn tạo ra ở trên. Tiếp đó, nhấn nút Download by URL để bắt
đầu quá trình là xong.
Kết luận
Là
một dịch vụ sử miễn phí nên nó có một số hạn chế về di chuyển tập tin,
chẳng hạn như kích thước tập tin không thể vượt quá 20 MB, và bạn chỉ có
thể chuyển 1024 MB dung lượng các tập tin trong một tháng.
Châu Quốc Hùng
Chuyển đổi PDF sang SWF quá đơn giản
14:09, Thứ Hai, 14/05/2012 (GMT+7)
Bạn đang có một số tài liệu định dạng PDF và muốn chia sẻ nó mọi
người trên blog/website cá nhân của mình với hình thức đọc trực tiếp.
Bạn có thể upload lên các dịch vụ chia sẻ tài liệu rồi lấy mã HTML để
chèn vào blog/website, nhưng bạn muốn chủ động hơn, không muốn phụ thuộc
vào các dịch vụ khác. 3DPageFlip PDF to Flash là phần mềm khá hữu ích cho bạn lúc này.



3DPageFlip PDF to Flash
là phần mềm cho phép bạn chuyển đổi hàng loạt tập tin PDF sang định
dạng SWF để bạn chèn vào blog/website như một mã Flash thông thường.
Bạn có thể tải về 3DPageFlip PDF to Flash về miễn phí tại đây.
Sau khi cài đặt và khởi động ứng dụng, bạn sẽ được ứng dụng cung cấp cho 3 chế độ làm việc:
- Batch Convert Mode: chế độ chuyển đổi các tập tin PDF được lựa chọn sang SWF thông thường
- Hot Directories Mode: chế độ chuyển đổi các tập tin PDF cho trong một thư mục sang đinh dạng SWF
- Command Line Mode: chế độ chuyển đổi bằng dòng lệnh
Tùy
theo nhu cầu sử dụng bạn lựa chọn chế độ làm việc cho phù hợp. Lựa chọn
chế độ Batch Convert Mode để chuyển các tập tin PDF bình thường, sau
khi lựa chọn chế độ này, bạn tiếp hành kéo thả các tập tin PDF cần
chuyển đổi vào khung trống ở cửa sổ làm việc kế tiếp.
Sau
khi đã lựa chọn các tập tin hoàn tất, bạn nhấn nút Convert để ứng dụng
bắt đầu chuyển đổi. Thời gian chuyển đổi nhanh hay chậm là tùy thuộc vào
độ phức tạp của tập tin PDF, tập tin PDF có nhiều hình ảnh sẽ chuyển
đổi lâu hơn tập tin PDF văn bản thông thường.
Đối
với chế độ Hot Directories Mode, bạn tiến hành thiết lập thư mục chứa
các tập tin PDF tại trường Input và thư mục chứa các tập tin SWF tại
trường Output, nơi lưu trữ tập tin Log tại trường Log File. Sau khi đã
thiết lập xong, bạn nhấn nút Play màu xanh ở bên dưới để bắt đầu quá
trình chuyển đổi.
3DPageFlip PDF to Flash tương thích với Windows XP, Windows Vista, Windows 7 và Windows 8. Thử nghiệm lỗi trên Windows 7 64-bits.
Lê Dương Viễn Chinh








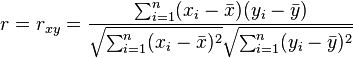
 được cho như trên
được cho như trên (trung bình mẫu của {x1,...,xn}) ; tương tự cho $\bar{y}$
(trung bình mẫu của {x1,...,xn}) ; tương tự cho $\bar{y}$ 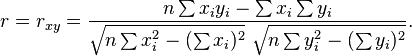

 được cho như trên
được cho như trên
 được định nghĩa như sau
được định nghĩa như sau là số tiêu chuẩn của x (tương tự cho y)
là số tiêu chuẩn của x (tương tự cho y)
 (độ lệch tiêu chuẩn của x); (tương tự cho sy )
(độ lệch tiêu chuẩn của x); (tương tự cho sy )


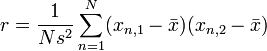 ,
,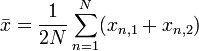 ,
, .
.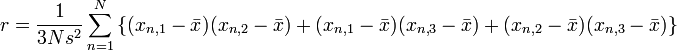 ,
, ,
, .
.
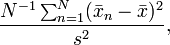








 , là sai biệt giữa 2 bậc của mỗi quan sát
, là sai biệt giữa 2 bậc của mỗi quan sát 
 . Tổng số quan sát n = 10. Thay các trị số vào công thức :
. Tổng số quan sát n = 10. Thay các trị số vào công thức :


















