Vật chất toán học .

Vật chất ở thể mới: Vật chất toán học

Theo Wikipedia

Chúng ta đã có chất rắn, chất lỏng, chất khí, dạng plasma và thể Bose-Einstein . Có vẻ như thời điểm chúng ta phát hiện ra dạng vật chất chủ đạo - một dạng mới của vật chất – dựa hoàn toàn vào toán học, đã đến.

Nils Bass, nhà toán học tại Đại học Khoa học và Kĩ thuật Na uy ở Trondheim đã phát hiện ra một phương thức mới để các thành phần vật chất liên kết với nhau.

Ông đã phát hiện điều này khi nghiên cứu lĩnh vực hình dạng học ( topology ) – ngành khoa học về tính chất của vật chất mà các vật thể có chung nhờ vào hình dáng của chúng.

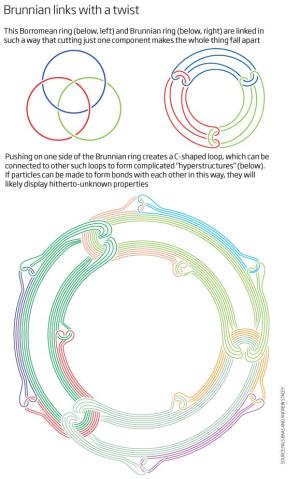
Vòng Borrom (dưới, trái) và Brun (dưới, phải) được liên kết theo kiểu nếu chỉ cắt một phần, toàn bộ vòng sẽ bị tách rời.

Tác động vào một mặt của vòng Brun để tạo ra một hình chữ C, những chữ C này liên kết với nhau để tạo ra “siêu cấu trúc” phức tạp (dưới, to). Nếu các hạt được kết nhóm theo cách này, chúng sẽ thể hiện những tính chất chưa từng được biết tới từ trước đến nay.

Nó liên quan tới các hình dạng đa dạng của vật chất khi chúng ta nén hoặc uốn chúng. Ví dụ, một chiếc bánh rán và một chén trà có chung hình tròn, thuật ngữ chuyên môn gọi là cùng hình dạng học. Chúng ta cũng có thể nặn cái bánh rán thành hình chén trà nếu muốn.

Bass đang nghiên cứu vòng Brun – tập hợp các vòng tròn được liên kết với nhau nhưng sẽ bị tách ra nếu chỉ một vòng tròn bị tách. Tiêu biểu nhất của loại liên kết này là vòng Borrom . Cứ hai trong ba vòng lại nối với nhau ở một đầu, và cắt một vòng thôi sẽ phá vỡ tất cả liên kết.

Bass chỉ ra rằng rất nhiều kiểu liên kết có thể được hình thành theo cách này. Không chỉ là có bốn, năm thành phần hay nhiều hơn, mà sự liên kết của nhiều tổ hợp liên kết này với nhau cũng theo kiểu Brun tạo ra cái mà Bass gọi là “Siêu cấu trúc”.

Năm 1970, Vitany Efimov tiên đoán liên kết ba Borrom có thể được phản ánh trong tự nhiên ở dạng nhóm ba yếu tố chưa được phát hiện ngày ấy. Những nhóm như vậy gần đây đã được tìm thấy trong vật lý.

Năm 2006, “Trạng thái Efimov” được tìm thấy ở khí nguyên tử cesium siêu lạnh: mỗi nguyên tử nối với từng nguyên tử còn lại, và tháo một mối nối thì tất cả liên kết tan rã.

Năm 2010, các nhà nghiên cứu Nhật Bản tìm thấy vòng Borrom ở liên kết giữa các nguyên tử lượng tử. “Những cấu trúc này phục vụ như một công thức cho những gì chúng ta có thể tạo ra ở thế giới”, Bass nói.

Nhưng siêu cấu trúc phức tạp của Bass có một sự khác biệt căn bản về hình dạng học ( topology ) với tất cả những thứ ở trong tự nhiên. Nếu những nhóm hạt được cấu trúc theo cách này, chúng sẽ tạo ra những dạng vật chất mà chúng ta chưa từng thấy. Bass giảng giải: “Khi chúng ta đạt tới một cấp độ cao hơn, một thứ hoàn toàn mới xảy ra một cách đơn giản toán học – và tôi cho rằng điều này cũng sẽ xảy ra trong thế giới thực”.

Bass đã kết hợp với Ned Seeman của Đại học Newyork để tìm cách tạo ra siêu cấu trúc. “Toán học có vẻ là một nhà dự báo tốt của tự nhiên”, Seeman – người tổng hợp vòng Borrom từ các đoạn ADN năm 1997 chia sẻ. “Chúng tôi nghĩ rằng việc này sẽ thành công”.

Đọc tiếp ...

Bass có đầy đủ những con đường để hướng tới, bao gồm những khám phá căn bản của thuyết lượng tử. Khi các hạt tương tác với nhau, kể cả khi đã bị phân tách, chúng đươc tổng hợp tỉ mỉ trong một quá trình lượng tử gọi là “kết rối”. Nếu các hạt liên kết với nhau theo kiểu vòng Brun phức tạp, kể cả khi đã bị tách ra chúng vẫn có ảnh hưởng đến nhau. Điều này, Bass cho hay, mở ra những khả năng mới để tạo ra những liên kết ma kiểu như những con rối bị điều khiển bằng dây.

“Một khi (những liên kết này) được chỉ ra, chúng ta có thể quay lại và tìm chúng ở phương trình Schrodinger .” – phương trình miêu tả toán học của thuyết lượng tử, Bass dự đoán.

Từ đó, có thể tạo ra những trạng thái lượng tử mới tại các phòng thí nghiệm. Điều đó đến lượt nó lại mở ra những phương thức mới để sản xuất máy tính lượng tử siêu mạnh – thao tác với thông tin được mang trong trạng thái lượng tử của hạt. Những thông tin lượng tử như vậy có thể ở nhiều trạng thái trong cùng một thời điểm, vì thế máy tính lượng tử có thể thực hiện một lượng khổng lồ các phép tính cùng lúc.

Nguồn : 
http://khoahoc.baodatviet.vn/Home/KHCN/Vat-chat-o-the-moi-vat-chat-toan-hoc/20111/126513.datviet

-----------------------------------------------------------------------------------------------------------
Bổ sung : Về liên kết  Brun
Nguồn : http://www.knotplot.com/brunnian/

Brunnian Links

These are nontrivial links that become trivial if any number of components are removed. Below are examples of Brunnian links with three, four, and six components. Note that except for the four component link, these links are not in their minimal projection. The three component link (when in a minimal projection) is also known as the Borromean Rings. The six component link was constructed and relaxed using KnotPlot.

Liên kết Brunnian

Đây là những liên kết không tầm thường trở nên tầm thường nếu có một số bất kỳ các thành phần được loại bỏ. Dưới đây là ví dụ về liên kết Brunnian  với ba, bốn và sáu thành phần. Lưu ý rằng ngoại trừ các liên kết bốn thành phần, những liên kết này không phải là hình chiếu tối thiểu của chúng . Liên kết ba thành phần  (khi thuộc về một hình chiếu tối thiểu) cũng được biết đến như những chiếc khuyên Borromean ( ring ). Các liên kết sáu thành phần được xây dựng bằng cách sử dụng KnotPlot.

Brun 3

Brun 4

 

Oblique view

Side view

Top view
 Click vào clip dưới đây để xem một knot ( nút ) không tầm thường suy biến về một cấu hình khả dĩ  .

                                         


Click vào clip dưới đây để xem một unknot ( vành ) suy biến về một đường tròn .

Click vào clip dưới đây để xem một unknot ( vành )  xoắn suy biến về một đường tròn .

Chú thích :
* Unknot ( vành ) , còn được gọi là nút tầm thường (Rolfsen 1976, trang 51), là một vòng khép kín mà không thắt nút. Trong những năm 1930, Reidemeister lần đầu tiên đã chứng minh rằng nút tồn tại (  khác biệt hẳn với  unknot ) bằng cách phát hiện ra , ứng dụng chuyển động Reidemeister và tô màu mỗi phần của một sơ đồ nút bằng một trong ba màu cho trước .
* Knot ( nút ) : Trong toán học, một nút được định nghĩa là một đường cong khép kín không tự giao nhau, được nhúng vào trong ba chiều và không thể gỡ để tạo ra một vòng lặp đơn giản (tức là, unknot). Trong ứng dụng thông thường, nút có thể được gắn trong chuỗi và sợi dây thừng mà một hoặc nhiều sợi được mở ở hai bên của nút . Một nút có thể được tổng quát hoá thành một liên kết, có thể xem như là một bộ sưu tập thắt nút của một hoặc nhiều sợi khép kín .

-----------------------------------------------------------------------------------------------------------

MIỀN GIỚI HẠN CỦA 2 MẶT 3D .

The movie below was created in about five or ten minutes using the components. It simply shows the region between two surfaces, one of which is given by the instructor, and the other by the student. These occur naturally in discussing multiple integrals.

Công cụ nhỏ gọn này giúp chúng ta quan sát và mô tả những mặt 3D có phương trình z = f(x,y)

------------------------------------------------------------------------------------------------------------------ Chúng ta phải biết và chúng ta sẽ biết .