Phần 2 . Cách sử dụng .
Lời nói đầu .
Như chúng ta đã biết loạt bài " DANH MỤC CÁC ĐƯỜNG CONG " được trình bày trước đây gồm có 3 phần . Nội dung của những phần này là liệt kê các phương trình , tên gọi cùng các giai thoại và chú thích lịch sử của một số đường cong thường xuất hiện trong toán học , vật lý , thiên văn và nhiều ngành kỹ thuật khác .
Bạn đọc có thể theo dõi chi tiết trên các trang sau :
Phiên bản mới nhất đăng trên
http://tusach.thuvienkhoahoc.com/wiki/Danh_mục_và_lịch_sử_các_đường_cong
Tiếp theo sau đây là chuyên mục " KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D " ,
Mục đích của chuỗi bài viết này là khảo sát đồ thị các đường cong bằng các công cụ trực tuyến (online) hoặc trình ứng dụng ( phần mềm offline ) .
Việc thực hành này là hết sức cần thiết và cũng mang lại nhiều kết quả lợi ích . Một mặt nó giúp chúng ta hiểu rõ hơn về các tính chất đặc trưng của các đường cong , mặt khác cũng là dịp làm quen với một số trình ứng dụng có quy mô lớn và tốc độ xử lý rất mạnh . Từ đó chúng ta có thêm kiến thức về đồ họa phục vụ cho việc nghiên cứu hoặc giải quyết những bài toán cụ thể trong phạm vi chuyên môn của mình .
Xin trân trọng giới thiệu cùng bạn đọc .
Trần hồng Cơ
Ngày 20 /04/ 2014 .
-----------------------------------------------------------------------------------------------------------------------------------
I . VẼ ĐỒ THỊ BẰNG TRÌNH ỨNG DỤNG .
Trong bài viết này tác giả sẽ trình bày cách vẽ đồ thị đường cong bằng các trình ứng dụng Graphing Package , Xcas , wxMaxima và Maple V ( một trình ứng dụng khá tốt cho việc tính toán và vẽ đồ thị là CalculationCenter 2.0 , tuy nhiên các bạn phải có license cho chương trình này để khai thác đầy đủ các chức năng của nó ) . Đây là những phần mềm miễn phí đã được trình bày ở phần 1 . I .
1.1 Những bước chập chững đầu tiên .
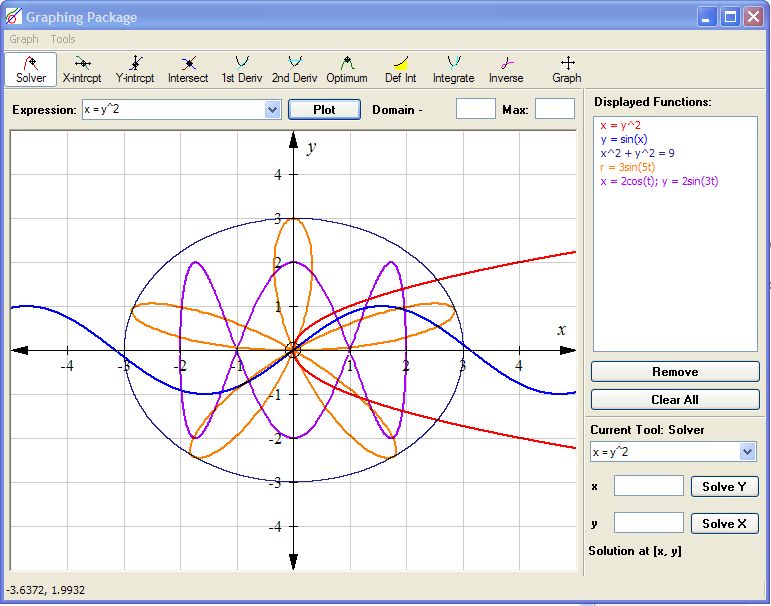
1.1.1 Graphing Package .
Sau khi đã tải về máy tính của bạn và giải nén , click vào GraphingPackage.exe ,
-Để chọn định dạng hàm số cần vẽ : bạn click vào ô Expression . Các dạng hàm mà GP có thể giúp chúng ta vẽ đồ thị là y = f(x) , x = f(y) , hàm ẩn F(x,y) , r = f(t) , hệ hàm x = f(t) ; y =g(t) .
- Tuyệt thật ! bây giờ chúng ta chỉ cần nhấn vào ô Plot là có ngay đồ thị hàm cần vẽ . Hãy nhìn thử xem - mời các bạn click vào hình nhỏ - cũng không đến nỗi tệ đâu phải không các bạn ?
-Để điều chỉnh các tọa độ trục , độ lớn của lưới , đặt tên cho trục các bạn click vào Graph và thay đổi các tham số maximum hay minimum của x axis , y axis .
-Để ghi lại hình ảnh đã vẽ các bạn click vào Graph và chọn Copy to clipboard rồi Paste vào trang word hoặc Paint để save lại .
1.1.2 Graphing Calculator 3D .
Sau khi đã tải về máy tính của bạn và cài đặt Graphing Calculator 3D , click vào
Giao diện của GC rất tốt , các bạn xem thử hình động dưới đây mô tả các chức năng đồ họa .
- Để vẽ hàm tham số click vào ô parametric , nhập x = f(u) và y = g(u) .
- Để vẽ hàm tọa độ cực click vào ô Polar , nhập r = f(θ)
Vì anh bạn TinTin GC giúp chúng ta miễn phí nên để lưu lại hình bạn dùng một trình chụp màn hình để lưu lại dạng jpg , png hay gif . Ở đây tác giả dùng phần mềm IrfanView . ( http://www.irfanview.com/ )
Xem hình minh họa dưới đây .
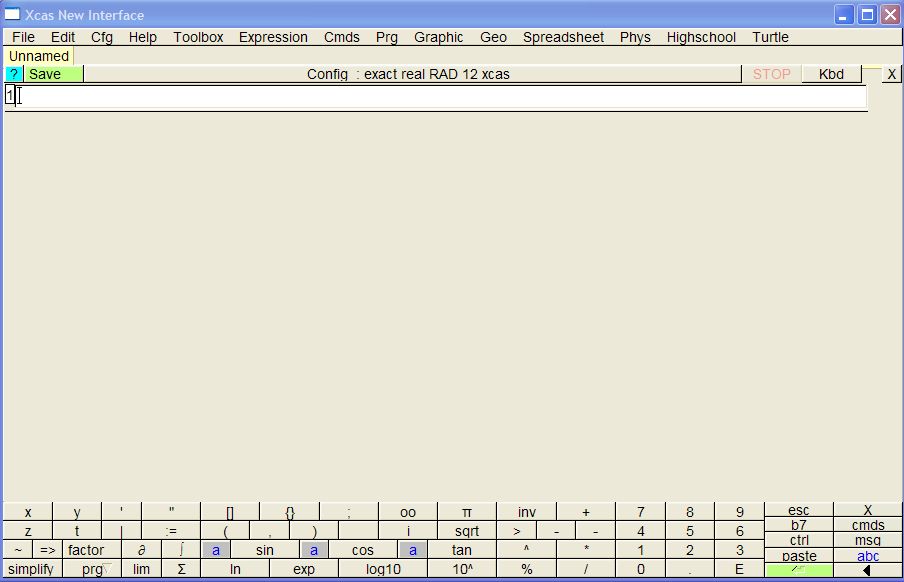
1.1.3 Giac/Xcas .
Sau khi đã tải về máy tính của bạn và cài đặt Xcas , click vào
Nhìn có vẻ không bắt mắt , nhưng các tính năng của Đấu sĩ GX này khá hữu hiệu . Để vẽ đồ thị các bạn click vào Graphic và chọn định dạng cho hàm số . Xem hình động sau để biết tính năng vẽ đồ thị của GX nhé !
Các bạn vào Graphic -> Curves ->
plotfunc : vẽ hàm một biến số
plotparam : vẽ hàm tham số 2d
plotpolar : vẽ hàm tọa độ cực
plotarea : tô màu miền dưới đường cong
plotimplicit : vẽ hàm ẩn
plotcontour : vẽ đường mức của hàm f(x,y)
plotdensity : vẽ đường mức hàm z 2d dạng phổ màu .
plotfunc : vẽ hàm một biến số
plotparam : vẽ hàm tham số 2d
plotpolar : vẽ hàm tọa độ cực
plotarea : tô màu miền dưới đường cong
plotimplicit : vẽ hàm ẩn
plotcontour : vẽ đường mức của hàm f(x,y)
plotdensity : vẽ đường mức hàm z 2d dạng phổ màu .
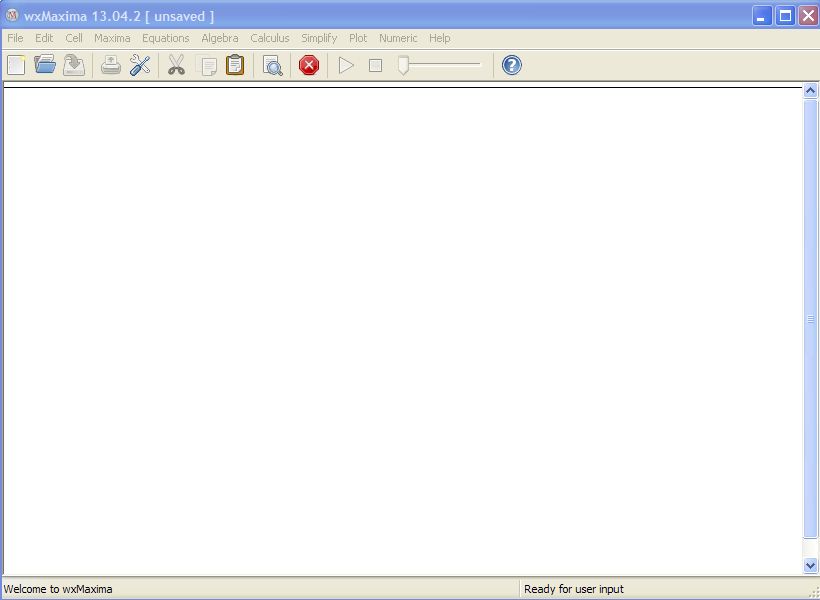
1.1.4 wxMaxima .
Sau khi đã tải về máy tính của bạn và cài đặt , click vào
Một số tính năng của wxM là khá tốt , nhưng bây giờ chúng ta hãy dành thời gian quan tâm đến phần vẽ đồ thị Plot . Các bạn click vào hình nhỏ xem hình động sẽ thấy những nét kỳ bí của anh chàng Hiệp sĩ wxM .
- Vào special chọn parametric plot để vẽ hàm tham số 2D .
-Chọn discrete vẽ đồ thị với nhập liệu rời rạc , mỗi số cách nhau dấu phẩy ( , )
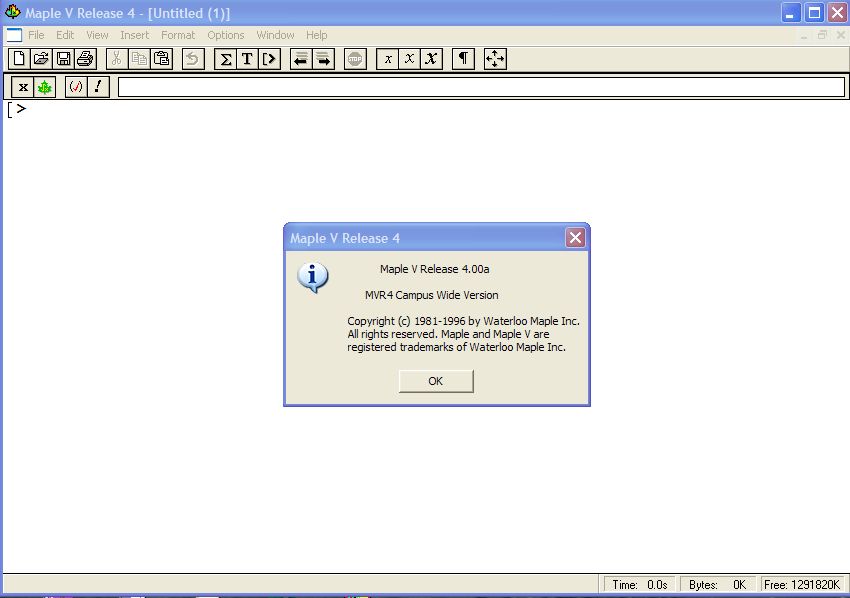
,1.1.5 Maple V .
Sau khi đã tải về máy tính của bạn và giải nén , bạn vào Maple V v4.0 \ BIN.WIN click vào
Trong phần 1.I các bạn đã được giới thiệu về Maple với các đặc trưng của nó , để thực hiện vẽ đồ thị chúng ta cần phải truy xuất gói công cụ plots , nhập lệnh >?plot ; click hình nhỏ để đọc hướng dẫn trước khi sử dụng .
1.2 Một số lệnh trong Maple V .
Trong những trình ứng dụng nêu trên chỉ có Bộ tứ Maple V là khá phức tạp như đã giới thiệu trong phần 1.I , đòi hỏi nhận lệnh trực tiếp từ người dùng , vì thế để chiều lòng Maple.V các bạn hãy khai thác gói công cụ plots nhé !
>with(plots):
1.2.1 Vẽ đồ thị dạng hàm số .
Cấu trúc lệnh
>plot(funcs,xint,yint,option1,option2);
+funcs : biểu thức chứa biến , hàm số { ... , ... , ... }
+xint : khoảng hoành độ
+yint : khoảng tung độ
+option1 , 2 :
axes : box , frame , none , normal ( trục )
color : red , blue , green , yellow , cyan ...
legend , linestyle , numpoints , thickness , title , titlefont , style , symbol , ...
1.2 Một số lệnh trong Maple V .
Trong những trình ứng dụng nêu trên chỉ có Bộ tứ Maple V là khá phức tạp như đã giới thiệu trong phần 1.I , đòi hỏi nhận lệnh trực tiếp từ người dùng , vì thế để chiều lòng Maple.V các bạn hãy khai thác gói công cụ plots nhé !
>with(plots):
1.2.1 Vẽ đồ thị dạng hàm số .
Cấu trúc lệnh
>plot(funcs,xint,yint,option1,option2);
+funcs : biểu thức chứa biến , hàm số { ... , ... , ... }
+xint : khoảng hoành độ
+yint : khoảng tung độ
+option1 , 2 :
axes : box , frame , none , normal ( trục )
color : red , blue , green , yellow , cyan ...
legend , linestyle , numpoints , thickness , title , titlefont , style , symbol , ...
1.2.2 Vẽ đồ thị dạng tham số .
Cấu trúc lệnh
>plot([x(t),y(t),t=t1..t2],option1,option2);
+[x(t),y(t)] : biểu thức chứa biến t , hàm số { ... , ... , ... }
+option1 , 2 :
axes : box , frame , none , normal ( trục )
color : red , blue , green , yellow , cyan ...
legend , linestyle , numpoints , thickness , title , titlefont , style , symbol , ...
Ví dụ . Vẽ đồ thị hàm tham số trong hệ Oxy .
Ví dụ . Vẽ đồ thị hàm tham số trong hệ tọa độ cực .
1.2.3 Vẽ đồ thị hàm ẩn .
Khai thác gói công cụ
>with(plots):
>with(plots, implicitplot):
Cấu trúc lệnh
>implicitplot(expr, x=a..b, y=c(x)..d(x), options);
>implicitplot(ineq, x=a..b, y=c(x)..d(x), options);
>implicitplot(f, a..b, c..d, options);
>implicitplot([expr1,expr2,t], x=a..b, y=c(x)..d(x), options);
+expr : biểu thức .
+options : tương tự như trên .
Xét các ví dụ sau .
Ví dụ . Vẽ đồ thị hàm ẩn trong hệ trục tọa độ cực không hiển thị màu
II . VẼ ĐỒ THỊ BẰNG CÔNG CỤ TRỰC TUYẾN .
Đối với hầu hết người sử dụng máy tính thì chuyện mở máy , nhập liệu , nhấn nút và thu thập thông tin một cách trực quan luôn là những điều thích thú vì nó tiết kiệm nhiều thời gian dành cho công việc . Điều này cũng có lý do chính đáng của nó nên các công cụ trực tuyến chính là món quà đặc biệt ( càng đặc biệt hơn nếu nó miễn phí ) dành cho chúng ta trong việc học tập , nghiên cứu và giảng dạy . Các bạn sẽ cùng với tác giả cùng tiếp tục cuộc hành trình khám phá những món quà trực tuyến dành cho việc khảo sát đường cong 2D với WA , Desmos , Seriesmathstudy , Flash&Math , MathsTools và FooPlot ( xem phần 1.II )
Chúng ta sẽ bắt đầu từ WolframAlpha ( tên tắt WA ) với phần Tra cứu các đường cong phẳng 2D . ( Xem phần 1.II - mục 2.1.1 )
2.1 Tra cứu đường cong phẳng .
2.1.1 Dùng WA .
Bạn chọn đường dẫn sau
http://www.wolframalpha.com/widgets/Plane Curves
Hay phần 1.II - mục 2.1.1
Ví dụ : Chọn đường cong astroid , sau đó nhấn Submit .
http://www.wolframalpha.com/widgets/know_about_any_scientist
nhập tên Johann Bernoulli và Gottfried Leibniz
2.1.2 Một vài website tra cứu về đường cong 2D .
1. http://www.2dcurves.com/
Đây là website chứa một bộ sưu tập đồ sộ gồm 939 đường cong 2D về nhiều khía cạnh khác nhau như , tên gọi , phương trình , lịch sử các nhà toán học , các ứng dụng liên quan . Bạn có thể truy tìm một đường cong theo năm cách : theo tên gọi , tìm kiếm nguyên văn , loại của phương trình , phương pháp dẫn xuất và bằng hình thức của đường cong . Tác giả của trang web này là Jan Wassenaar một chuyên gia IT , Viện Công nghệ và Dích vụ Thông tin , Hà lan .
2. http://curvebank.calstatela.edu/index/
National Curve Bank (NCB ) là một nguồn tài nguyên khoa học cho các học sinh , sinh viên khoa toán . NCB cung cấp các tính năng - ví dụ, hình ảnh động và những tương tác - mà một trang sách in thông thường không thể cung cấp cho người đọc . NCB cũng bao gồm hình học, đại số, và nhiều khía cạnh lịch sử của đường cong . Chính các loại thuộc tính này làm cho toán học trở nên đặc biệt hấp dẫn và làm phong phú thêm việc học tập trên lớp .
NCB hoan nghênh sự tham gia , khuyến khích gửi nhiều hình ảnh web động tốt nhất của bạn như là một "tài khoản" trong Ngân hàng Đường cong Quốc gia . NCB chủ trương sẵn sàng hợp tác trao đổi các kiến thức , kỹ năng kết hợp thông tin với các trang web nổi bật khác có cùng chủ đề về đường cong toán học .
Bạn đọc có thể tim hiểu thêm tại địa chỉ http://curvebank.calstatela.edu/home/home.htm .
3. http://www-history.mcs.st-and.ac.uk/history/Curves/Curves.html
Trang chủ này được khoa toán - thống kê , Đại học St Andrews . Đây là trường đại học đầu tiên của Scotland và lâu đời nhất đứng thứ ba trong khối quốc gia nói tiếng Anh, thành lập năm 1413. Website bao gồm nhiều nội dung cho phép chúng ta truy cập miễn phí như danh sách của hơn 1300 nhà toán học với tiểu sử trong kho lưu trữ , hơn 30 bài viết về lịch sử của các chủ đề khác nhau trong toán học từ cổ điển đến hiện đại . Các bạn có thể truy cập vào một danh sách gồm hơn 60 đường cong với lịch sử và các tính chất của chúng .
4. http://virtualmathmuseum.org/Curves/
Trang web này thuộc Nhóm phụ trách các dự án phát triển phần mềm 3D-XplorMath và dự án trang web Bảo tàng Toán học ảo (Virtual ) liên quan là 3DXM Consortium, đây là một nhóm tình nguyện viên quốc tế gồm các nhà toán học. Xem thêm chi tiết http://virtualmathmuseum.org/gallery4.html .
Consortium gửi lời chân thành cảm tạ sự hỗ trợ cho các dự án do Quỹ khoa học quốc gia (theo giải thưởng # 0.514.781) và bày tỏ lòng biết ơn khoa Toán của Đại học California tại Irvine về cơ sở lưu trữ các 3D-XplorMath và trang web Bảo tàng Toán học ảo .
Trang http://virtualmathmuseum.org/Curves/ này được duy trì bởi Richard Palais - giáo sư danh dự Đại học Brandeis . Các bạn có thể gửi email về bất kỳ vấn đề bạn tìm thấy với website này hoặc bất cứ đề nghị nào của bạn về sự đóng góp cải thiện nó .
Nếu có chút thời gian các bạn cũng nên ghé qua trang sau
http://vmm.math.uci.edu/3D-XplorMath/DocumentationPages/Curves.html
5. http://xahlee.info/SpecialPlaneCurves_dir/specialPlaneCurves.html
Trang chủ http://xahlee.info/index.html có 3400 bài viết bao gồm một số lĩnh vực như :Toán học & Lập trình, hướng dẫn và các bài tiểu luận.
Trang http://xahlee.info/math/math_index.html là danh mục các bài viết liên quan đến toán học. Có hơn một ngàn bài báo với những thông tin hết sức quan trọng và hữu ích . Các đề mục được liệt kê theo thứ tự tính chất của dự án. Những mục quan trọng thường được xếp trên đầu trang.
Trang http://xahlee.info/SpecialPlaneCurves_dir/specialPlaneCurves.html
được xem như một tự điển ảo về các đường cong đặc biệt chứa hơn 60 tập tin GeoGebra có thể được tải về miễn phí . Đặc biệt hơn nữa cuốn sách Curves and their properties của Robert Yate cũng có sẵn ở đây : http://xahlee.info/SpecialPlaneCurves_dir/_curves_robert_yates/yates_book.html
6. http://3d-xplormath.org/j/applets/en/index.html?utm_source=twitterfeed&utm_medium=twitter
3D-XplorMath-J là một chương trình chuyên dành cho "sự minh họa" , có thể xem đây là sự trực quan hóa của các đối tượng toán học. Nó được viết lại từ một chương trình tương tự như 3D-XplorMath, chạy trên các máy tính Macintosh. Xem http://3d-xplormath.org. 3D-XplorMath-J được viết bằng ngôn ngữ lập trình Java, đòi hỏi Java Phiên bản 5.0 hoặc cao hơn.
Trang web này cho thấy sự minh họa tương tự như chương trình Java , nhưng được trình bày theo hình thức "applet" để có thể xuất hiện trên một trang web. Applet cá nhân có thể được truy cập bằng cách nhấp vào liên kết trong danh sách điều hướng cột bên trái.
Lưu ý rằng phải mất một chút thời gian, sau khi bạn nhấp vào một trong các liên kết, applet sẽ được tải về và bắt đầu chạy.
7. http://www.mathcurve.com/
mathcurve.com là website bách khoa toàn thư toán học chuyên về đường , mặt và khối - trong đó có phần nghiên cứu về hình học fractal . Tác giả website này là Robert Ferreol , người đã có công biên tập nội dung từ 1993 và được cập nhật liên tục đến nay vì vậy nội dung rất phong phú . Ngoài những tài liệu tham khảo rất nhiều hình ảnh minh họa và ứng dụng trong thực tiễn cũng được trình bày khá chi tiết .
8. http://serge.mehl.free.fr/base/index_cbe.html
Đây cũng là website chuyên về các đường cong trình bày khá đầy đủ về phương trình , cách xây dựng quỹ tích điểm và mô hình áp dụng thực tế những công thức , bài toán có liên quan đến đường cong phẳng .
2.2 Vẽ đồ thị trực tuyến các đường cong phẳng .
2.2.1 Dùng WA .
Bạn chọn các đường dẫn sau từ phần 1.II - mục 2.1.2 - 2.1.5 - 2.1.6 - 2.1.8 - 2.1.9 và nhập liệu theo định dạng hàm số .
Ví dụ : Chọn đường cong astroid , dùng các widgets Plotter , Parametric Plot và Mini Plotter chúng ta thu được kết quả
2.2.2 Dùng DESMOS .
Bạn chọn đường dẫn https://www.desmos.com/calculator nhập liệu vào ô trắng . Các biểu thức có thể là hàm một biến , hàm ẩn hoặc hàm tọa độ cực .
Xem hình minh họa
Bạn có thể chọn tùy biến để vẽ hình động như sau
-Điểm mạnh của Demos là ta có thể tạo đồ thị động dựa trên sự kết hợp các biểu thức .
Ví dụ : đồ thị hàm spiral logarithm
( Xem chi tiết : https://lh4.googleusercontent.com/LOG+SPIRAL_DESMOS_Graphic.gif )
2.2.3 Dùng Seriesmathstudy .
Bạn chọn đường dẫn http://graph.seriesmathstudy.com/
hoặc http://vietgraph.seriesmathstudy.com/
Sau khi click vào StartGraphFunc giao diện của chương trình như sau
. Các biểu thức nhập liệu là hàm một biến f(x) , hàm tọa độ cực , hoặc hàm tham số . Seriesmathstudy cho phép chúng ta nhập và vẽ 5 hàm số cùng một lúc ( click vào Multiple Graphs ,nhập hàm và nhấn Graph It ! ) và đồng thời cho ảnh động 3D minh họa cho đồ thị hàm số 2D ( click vào View 3D ) .
Xem hình động minh họa các chức năng của GraphFunc .
2.2.4 Dùng Flash&Math .
Bạn chọn đường dẫn http://www.flashandmath.com/mathlets/index.html
hoặc http://www.math.uri.edu/~bkaskosz/flashmo/
-Chọn vẽ các hàm đơn giản :
http://www.flashandmath.com/basic/simplegraph/index.html
http://www.flashandmath.com/mathlets/calc/fungraph/
( Công cụ này dùng để minh họa cho bài toán khảo sát hàm số khi dạy trực tuyến thì thật là tuyệt vời )
http://www.flashandmath.com/mathlets/calc/param2d/
hoặc http://www.math.uri.edu/~bkaskosz/flashmo/parcur/
-Chọn vẽ đồ thị hàm ẩn
http://www.flashandmath.com/mathlets/calc/implicit/
2.2.5 Dùng MathsTools .
Bạn chọn đường dẫn http://www.mathstools.com/section/main/functions_plotter#.U2C0DZGspMg
hoặc http://www.mathstools.com/
Mã nhúng :
<iframe src="http://www.mathstools.com/section/widget/functions_plotter" width="890" height="546" style="margin: 0; padding: 0;" scrolling="no"></iframe>
-Chọn hàm thông thường analytic , các bạn nhập biểu thức f(x) , nhấn plot .
-Chọn hàm tham số , click vào Parametric Form
-Chọn dãy hàm , click Function Succession
2.2.6 Dùng FooPlot .
Bạn chọn đường dẫn
http://fooplot.com
http://old.fooplot.com/index3d.php\
Để xem các tính năng của FooPlot mời các bạn xem hình minh họa động dưới đây
Khi đã có đồ thị hàm số FooPlot cho phép chúng ta save hình ảnh đồ thị theo định dạng . svg , eps , pdf và png ( Click vào Export as ... và download )
Để tạo đường link cho đồ thị hàm số đã cho , các bạn click vào Permanent .
-----------------------------------------------------------------------------------------------------------------------------------
III . LỜI KẾT .
Các bạn thân mến , trong phần 2 này tác giả đã đưa ra những kiến thức cần thiết để bước đầu chúng ta làm quen và tìm hiểu ( dù chỉ là sơ sài ) những tính năng kỹ thuật của các trình ứng dụng và công cụ đồ họa trực tuyến . Hy vọng những nội dung này sẽ góp phần giải quyết những khó khăn trong việc khảo sát thực nghiệm những đường cong trong các phần tiếp sau . Thời gian tới chúng ta sẽ cùng thực hành phác họa cụ thể đồ thị những đường cong này theo thứ tự danh mục của bài viết trước đây .
Cám ơn các bạn đã đọc bài viết này . Hen gặp lại .
Trần hồng Cơ
Ngày 27 /04/ 2014 .
-------------------------------------------------------------------------------------------
Khoa học là một điều tuyệt vời khi không phải dùng nó để kiếm sống.
Albert Einstein .
Không có nhận xét nào :
Đăng nhận xét
Cám ơn lời bình luận của các bạn .
Tôi sẽ xem và trả lời ngay khi có thể .
I will review and respond to your comments as soon as possible.,
Thank you .
Trần hồng Cơ .
Co.H.Tran
MMPC-VN
cohtran@mail.com
https://plus.google.com/+HongCoTranMMPC-VN/about