GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN . Phần 15c . HÀM SỐ MŨ - PHƯƠNG TRÌNH MŨ.

GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN .

Phần 15c . HÀM SỐ MŨ  - PHƯƠNG TRÌNH MŨ.   

DANH MỤC CÔNG CỤ GIẢI TOÁN TRỰC TUYẾN  MATHEMATICA  WOLFRAM | ALPHA .

Giới thiệu .

Bạn đọc truy cập vào đường dẫn  http://cohtrantmed.yolasite.com/widgets-tructuyen  để sử dụng các widgets giải toán trực tuyến W|A Mathematica theo chỉ mục trong danh sách dưới đây .

Những widgets này đã được tác giả sắp xếp theo từng môn học và cấp lớp theo ký hiệu như sau :

D : Đại số . Ví dụ  D8.1 widget dùng cho Đại số lớp 8 , mục 1 - Khai triển , rút gọn biểu thức đại số .
H : Hình học . Ví dụ  H12.3  widget dùng cho Hình học lớp 12 , mục 3 - Viết phương trình tham số của đường thẳng trong không gian .
G : Giải tích . Ví dụ : G11.7  widget dùng cho Giải tích lớp 11 , mục 7 - Tính đạo hàm cấp cao của hàm số
GI : Giải tích cao cấp I . Ví dụ GI.15  widget dùng cho Giải tích cao cấp I , mục 15 - Khai triển hàm số bằng đa thức TAYLOR
GII : Giải tích cao cấp II .


++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


 ĐẠI SỐ 8

D8.1  Khai triển , rút gọn biểu thức đại số
D8.2  Rút gọn phân thức
D8.3  Phân tích thừa số
D8.4  Nhân 2 đa thức
D8.5  Khai triển tích số ( có thể dùng để khai triển Newton )
D8.6  Phân tích thừa số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 10

D10.1 Giải phương trình nguyên Diophante
D10.2 Giải phương trình tuyệt đối
D10.3 Giải phương trình chứa tham số
D10.4  Giải phương trình đại số
D10.5  Giải phương trình từng bước
D10.6  Giải bất phương trình minh hoạ bằng đồ thị

D10.8  Tính giá trị biểu thức hàm số
D10.9  Giải bất phương trình đại số và minh hoạ bằng đồ thị
D10.10  Giải bất phương trình đại số - tìm miền nghiệm
D10.11  Giải phương trình đại số
D10.12  Giải phương trình vô tỷ
D10.13  Giải phương trình minh hoạ từng bước
D10.14  Giải phương trình dạng hàm ẩn
D10.15  Giải hệ thống phương trình tuyến tính , phi tuyến
D10.16  Giải hệ phương trình
D10.17  Vẽ miền nghiệm của bất phương trình đại số
D10.19  Tối ưu hoá hàm 2 biến với các ràng buộc
D10.20  Tìm giao điểm của đồ thị hàm số và trục hoành Ox , trục tung Oy

HÌNH HỌC 10

H10.1  Tính diện tích tam giác trong hệ toạ độ Oxy
H10.3  Khảo sát conic ( đường tròn , Ellipse , Parabola , Hyperbola )
H10.2  Tính khoảng cách từ 1 điểm đến đường thẳng trong Oxy



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 11

D11.1 Thuật chia Euclide dùng cho số và đa thức  ( HORNER )
D11.2  Tính tổng nghịch đảo của n số tự nhiên




D11.6  Khai triển nhị thức Newton


GIẢI TÍCH 11


G11.1  Tính gíá trị một chuỗi số  theo n
G11.2  Đa thức truy hồi
G11.3  Khảo sát tính hội tụ của chuỗi số
G11.4  Tính giới hạn của chuỗi số khi  $n \rightarrow  \infty$
G11.5  Tìm hàm số ngược của hàm số cho trước
G11.6  Tìm đạo hàm của hàm số hợp - giải thích
G11.7   Tính đạo hàm cấp cao của hàm số
G11.8   Tìm giới hạn của hàm số
G11.9   Tìm giới hạn của hàm số
G11.10  Tính đạo hàm hàm số có dạng U/V
G11.11  Tìm đạo hàm của hàm số cho trước
G11.12  Tìm đạo hàm của hàm số cho trước

G11+12.1   Tính đạo hàm ,tích phân , giới hạn , vẽ đồ thị


LƯỢNG GIÁC 11

L11.1   Giải phương trình lượng giác
L11.2   Giải phương trình lượng giác trên một đoạn
L11.3   Tìm chu kỳ của hàm số tuần hoàn
L11.4   Khai triển công thức lượng giác



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 12

D12.1   Cấu trúc của số phức
D12.1   Giải phương trình mũ
D12.3   Giải  phương trình chứa tham số
D12.4   Giải  phương trình  bất kỳ  ( Bậc 2 , 3 , ... , mũ  , log , căn thức )
D12.5   Giải phương trình mũ



GIẢI TÍCH 12


G12.1  Vẽ đồ thị biểu diễn phương trình
G12.2    Khảo sát hàm số hữu tỷ
G12.3   Vẽ đồ thị trong toạ độ cực (Polar)
G12.4    Tìm cực trị của hàm số
G12.5    Vẽ đồ thị hàm số 2D
G12.6   Tìm đạo hàm cấp 2 của hàm số
G12.7    Vẽ nhiều hàm số - Basic plot. To plot two or more functions, enter {f1(x), f2(x),...}
G12.8    Tìm điểm uốn của hàm số cho trước
G12.9    Tìm nghiệm của các phương trình  y = 0 , y ' = 0 ,  y " = 0
G12.10    Tính tích phân bất định
G12.11    Tính tích phân bất định minh hoạ từng bước
G12.12   Tính tích phân bất định minh hoạ từng bước
G12.13   Tìm đường tiệm cận của hàm số
G12.14   Tính diện tích hình phẳng giới hạn bởi 2 đường cong (C1) , (C2)
G12.15  Tìm giao điểm của hàm số đa thức và trục hoành Ox - Vẽ đồ thị .
G12.16    Tính thể tích vật thể tròn xoay giới hạn bởi (C1) , (C2)
G12.17    Vẽ đồ thị hàm số ( có đường tiệm cận )
G12.18   Vẽ đồ thị 2D , 3D
G12.19   Tìm hoành độ giao điểm giữa 2 đường cong (C1) , (C2)
G12.20    Vẽ đường cong tham số 3D
G12.21    Tính diện tich mặt tròn xoay
G12.22    Tích thể tích vật tròn xoay  (C) , trục  Ox , x =a , x= b
G12.23    Thể tích vật tròn xoay
G12.24    Tích thể tích vật tròn xoay (C1) , (C2) , trục OX , x = a , x = b
G12.25    Khảo sát hàm số đơn giản
G12.26    Tìm cực trị của hàm số
G12.27    Tìm nguyên hàm của hàm số
G12.28    Tính tích phân xác định


HÌNH HỌC 12

H12.1  Tính khoảng cách 2 điểm trong 2D , 3D
H12.2   Viết phương trình mặt phẳng qua 3 điểm trong không gian
H12.3  Viết phương trình tham số của đường thẳng trong không gian
H12.4   Tìm công thức thể tích , diện tích hình không gian
H12.5   Vẽ đồ thị 2D , mặt 3D
H12.6    Tích có hướng 2 vector



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

GIẢI TÍCH CAO CẤP

GI.1    Vẽ đồ thị , mặt 3D
GI.2   Vẽ đồ thị , mặt  3D
GI.3    Tích phân 2 lớp
GI.5    Tích phân kép
GI.6    Tích phân bội 3
GI.7    Tích phân bội 3
GI.8    Tích phân suy rộng
GI.9    Chuỗi và dãy số
GI.10    Các bài toán cơ bản trong vi  tích phân
GI.11     Vẽ hàm từng khúc ( piecewise ) - dùng để xét tính liên tục của hàm số
GI.12    Tính đạo hàm và tích phân một hàm số cho trước
GI.13     Vẽ đồ thị hàm số trong hệ toạ độ cực
GI.14     Tính đạo hàm riêng
GI.15    Khai triển hàm số bằng đa thức TAYLOR
GI.16    Tính tổng chuỗi số  n = 1...$\infty$
GI.17     Vẽ  đồ thị  3 hàm số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Bài viết sau đây mô tả các khái niệm toán học và hướng dẫn tính toán chi tiết bằng công cụ trực tuyến , bạn đọc có thể tham khảo những nội dung chính yếu được đề cập đến trong giáo trình toán phổ thông  cùng với các ví dụ minh họa  .

Một số website hữu ích phục vụ cho việc giảng dạy và học tập môn toán :

http://quickmath.com/
http://analyzemath.com/
http://www.intmath.com/
http://www.mathportal.org
https://www.mathway.com/
https://www.symbolab.com/
http://www.graphsketch.com/
http://www.meta-calculator.com/online/?home
http://cohtrantmed.yolasite.com/widgets-tructuyen

https://www.geekandnerd.org/mathematics-problem-solver-online/

https://www.geekandnerd.org/edu-courses/

15.  HÀM SỐ MŨ - PHƯƠNG TRÌNH MŨ - Phương trình mũ .

15.2  Phương trình mũ .

 
AL121.2a .Exponential equations _ Phương trình mũ 

Followings are methods often used to solve exponential equations . Some of them were presented in previous flashcards AL121.1 a,b,c related to the exponent properties also remarked for matching systematically in order students could grasp the key methods in solving exponential equations easily .

Sau đây là những phương pháp thường được sử dụng để giải phương trình mũ .Một số phương pháp trong đó đã được trình bày ở Flashcards trước đây AL121.1 a, b, c liên quan đến tính chất hàm số mũ cũng được lưu ý một cách hệ thống để học sinh có thể nắm bắt được phương pháp chính trong việc giải quyết phương trình mũ một cách dễ dàng.

Author :

Co.H.Tran
MMPC VN
Copyright 2010
http://cohtranhsed.yolasite.com


   
15.2.2  Cách giải chi tiết phương trình mũ  $F(a^{f(x)},b^{g(x)})=C$   .
a. Phân loại  .

1. Basic form ( dạng cơ bản )
2. Polynomial form ( dạng đa thức )
3. Bases-product form ( dạng cơ số tích )
4. Irrational Cofactor form ( dạng cơ số lượng liên hiệp )
5. Two-Bases form ( dạng 2 vế hai cơ số )
6. Logarithmization form ( dạng logarith hóa )
7. Expo-Poly form ( dạng mũ - đa thức )
8. Expo-Log form ( dạng mũ - log )
9. Expo-Inverse form ( dạng mũ cơ số đảo )
10. Factorization form ( dạng tích số )



b. Cách giải chi tiết .

1.Phương trình mũ cơ bản .
$a^u = a^v  \Leftrightarrow  a  > 0 ; a \neq 1; u = v$
Dạng cơ bản , đưa về cùng cơ số .
Lưu  ý điều kiện cơ số và các điều kiện khác .

 

1. Basic form : ( dạng cơ bản , đưa về cùng cơ số , lưu ý điều kiện cơ số và các điều kiện khác )

au = av

<=> { 0 < a =/= 1 ; u = v }

a : base _ u , v : exponents

Ex :

23 - x = 16

3x +2 . 23 - x = 122x + 5 

2.Phương trình mũ quy về đa thức .
$At^2+Bt+C=0 , A \neq 0 ; t = a^{f(x)} ; t >0$
$At^3+Bt^2+Ct+D=0 , A \neq 0 ; t = a^{f(x)} ; t >0$
Dạng đa thức bậc 2,3 ... đặt  t =  hs mũ ,  t > 0 .
Đưa về phương trình bậc 2 , 3 .

 

2. Polynomial form : ( Dạng đa thức bậc 2,3 ... đặt t = hs mũ , t > 0 , đưa về phương trình bậc 2 , 3 )

At2 + Bt + C = 0

At3 + Bt2 + Ct + D = 0

a : base _ x : exponent

Let t = ax ( t > 0 )

Ex :

4x - 2 = 2x

27x - 32x+1 + 2.3x = 0 

3.Phương trình mũ cơ số tích .
$A.a^{2x}+B.b^{2x}+C.(ab)^x=0 ; a  , b> 0 ; a , b \neq 1$
Dạng cơ số tích , trong phương trình có 1 cơ số = tích 2 cơ số kia  .
Chia 2 vế cho cơ số nhỏ số mũ lớn .
Đặt  t =  hs mũ ,  t > 0 , đưa về phương trình bậc 2 .

 

3. Bases-product form : ( Dạng cơ số tích , trong phương trình có 1 cơ số = tích 2 cơ số kia , chia 2 vế cho cơ số nhỏ số mũ lớn , đặt t = hs mũ , t > 0 , đưa về phương trình bậc 2 )

A.a2x + B.b2x + C.(a.b)x = 0

a , b , a.b : bases _ x : exponent

Divide both sides by a2x

[ or b2x ] 

Ex :

5.4x + 2.25x = 7.10x

3.4x - 2.6x - 9x = 0 

4.Phương trình mũ cơ số lượng liên hiệp .
$(\sqrt{A}+\sqrt{B})^x+(\sqrt{A}-\sqrt{B})^x=k.C^x ; A,B>0 ;   \sqrt{A} \pm \sqrt{B} >0 ; \sqrt{A} \pm \sqrt{B} \neq 1$
Dạng cơ số lượng liên hiệp có 2 cơ số chứa căn +,-
bt (-) = k / bt(+)  , với k = tích 2 cơ số lượng liên hiệp .
x : exponent ( số mũ)

 

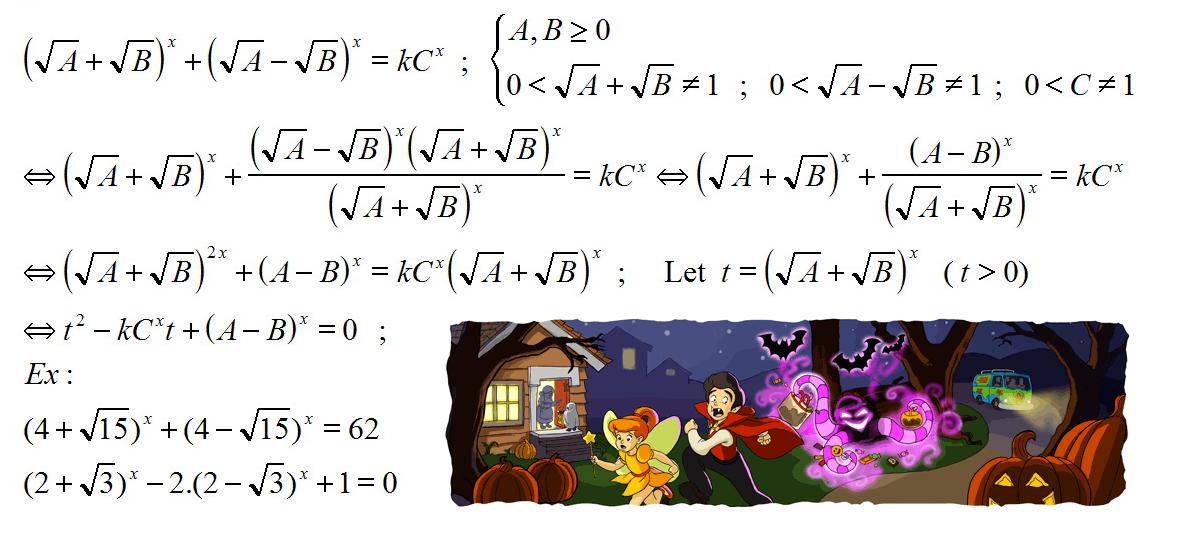
4.Irrational Cofactor form :

( dạng cơ số lượng liên hiệp , bt (-) = k / bt(+) , với k = tích 2 cơ số lượng liên hiệp )

x : exponent ( số mũ)

[ Dạng cơ số lượng liên hiệp có 2 cơ số chứa căn +,- ]

5.Phương trình mũ 2 vế 2 cơ số khác nhau .
$f(a^x,b^x)=g(a^x,b^x) ; a  , b> 0 ; a , b \neq 1$
$ \Leftrightarrow M.F(a^x)=N.G(b^x) \Leftrightarrow F(a^x)/G(b^x) =N/M ;  G(b^x) \neq 0 ; M \neq 0 $
Dạng 2 vế 2 cơ số khác nhau .
Chuyển các cơ số giống nhau về 1 vế , rút thừa số chung .
T/P  =  P/T

 
5. Two-Bases form : ( dạng 2 vế 2 cơ số khác nhau , chuyển các cơ số giống nhau về 1 vế , rút thừa số chung , T/P = P/T )

6.Phương trình mũ - logarith hóa .
$a^{kx+h}.b^{mx+n}.c^{rx+s}=Q; a,b,c>0;a,b,c \neq 1;Q=a^t.b^u.c^v \neq 0$
$\LARGE  \Leftrightarrow   \frac{ a^{kx+h}.b^{mx+n}.c^{rx+s}}{a^t.b^u.c^v} =1 $
$ \Leftrightarrow  a^{kx+h-t}.b^{mx+n-u}.c^{rx+s-v} =1$
Dạng logarith hóa có nhiều cơ số nguyên tố khác nhau .
Đưa vế phải = 1 , lấy log hai vế theo cơ số nhỏ .
Hạ mũ , rút thừa số chung , đưa về phương trình tích số .

 
6. Logarithmization form :( dạng log hóa có nhiều cơ số nguyên tố khác nhau , đưa vế phải = 1 , lấy log hai vế theo cơ số nhỏ , rút thừa số chung , đưa về phương trình tích ) 

7.Phương trình mũ - đa thức .
$h(a^x)=g(x) ; a >0; a \neq 1 \Leftrightarrow  y = h(a^x)-g(x) =0$
$\begin{cases}
 & h(a^x)\leftarrow  \wedge  g(x) \rightarrow   \\
 & h(a^x)\rightarrow  \wedge  g(x) \leftarrow
\end{cases}$
$\exists x_0  :   h(a^{x_0})-g(x_0) =0$
Dạng mũ -đa thức  hỗn hợp , trong phương trình có hàm số mũ và hàm số đa thức .
Giải bằng tính đơn điệu của hàm số .



8.Phương trình mũ - logarith .
$F(a^x,log_{b}x)=0 ;  a,b >0 ; a,b \neq 1 ; t = a^x ; t>0$
Dạng mũ -log hỗn hợp , trong phương trình có hàm số mũ chứa hàm log .
Đặt  t = hs mũ  , t > 0

 
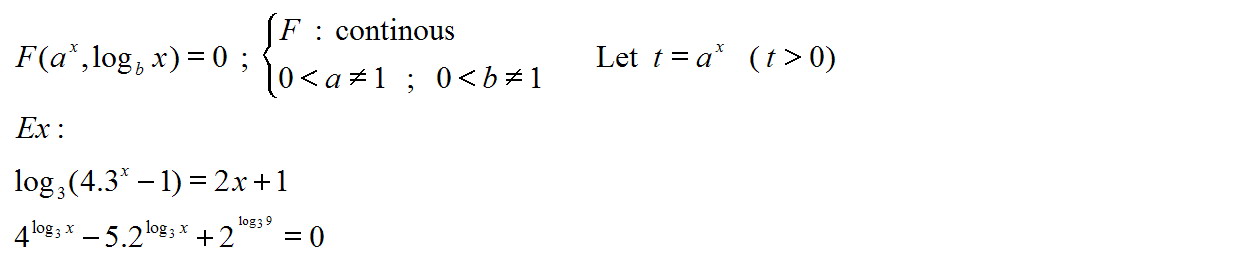
8. Expo-Log form : ( dạng mũ -log hỗn hợp , trong phương trình có hàm số mũ chứa hàm log , đặt t = hs mũ , t > 0 )

9.Phương trình mũ - cơ số đảo .
$A.a^x+B.a^{-x}=C ;  a>0 ; a \neq 1; t = a^x ; t>0$
Dạng mũ -cơ số đảo , trong phương trình có hàm mũ chứa 2 cơ số có thể đảo ngược .
đặt t = hs mũ

 
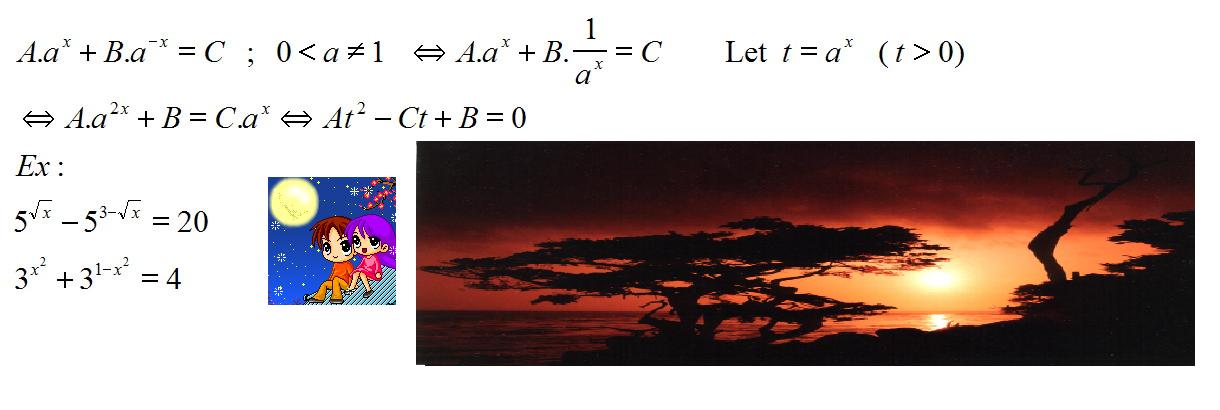
9. Expo-Inverse form : ( dạng mũ -cơ số đảo , trong phương trình có hàm mũ chứa 2 cơ số có thể đảo ngược , đặt t = hs mũ )

10.Phương trình mũ - tích số .
$F(A.a^x,B.b^x)=C ;  a,b >0 ; a,b \neq 1 \Leftrightarrow  F_1(a^x).F_2(b^x)=0$
Dạng mũ - tích số hỗn hợp , trong phương trình có hàm số mũ với các cơ số khác nhau .
Phân tích thừa số bằng cách nhóm số hạng $ ++ , +- , --$  .

 

10. Factorization form : ( dạng mũ - tích số hỗn hợp , trong phương trình có hàm số mũ với các cơ số , có thể phân tích thừa số )

b. Bài giải chi tiết các ví dụ .

 

AL121.2b .Examples for AL121.2a _Các ví dụ phương trình mũ

We present the solutions of exponential equations that are considered in flashcard AL121.2a . By using 10 methods students would be guided from easy and simple to many complex problems . Author hopes that always we feel very cool when studying and also creating many good ways for solving exponential equations .

Trong flashcard này ta sẽ trình bày lời giải các phương trình mũ đã xét ở AL121.2a . Bằng cách dùng 10 phương pháp , học sinh sẽ được hướng dẫn từ các bài toán đơn giản đến phức tạp . Tác giả hy vọng chúng ta luôn thoải mái khi học toán cũng như sáng tạo được nhiều cách giải tốt các phương trình mũ . 

Author :
Co.H.Tran
MMPC VN
Copyright 2010
http://cohtranhsed.yolasite.com

=======================

1. Basic form ( dạng cơ bản )

2. Polynomial form ( dạng đa thức )

3. Bases-product form ( dạng cơ số tích )

4.Irrational Cofactor form ( dạng cơ số lượng liên hiệp )

5. Two-Bases form ( dạng 2 vế hai cơ số ) 

6. Logarithmization form ( dạng logarith hóa ) 

7. Expo-Poly form ( dạng mũ - đa thức ) 

8. Expo-Log form ( dạng mũ - log )

9. Expo-Inverse form ( dạng mũ cơ số đảo )

10. Factorization form ( dạng tích số )

Xem các ví dụ minh họa trong Flashcard trên .

Ví dụ 1. 
Giải phương trình mũ cơ bản .

(i) $2^{3-x}=16$

(ii) $3^{x+2}.2^{3-x}=12^{2x+5}$

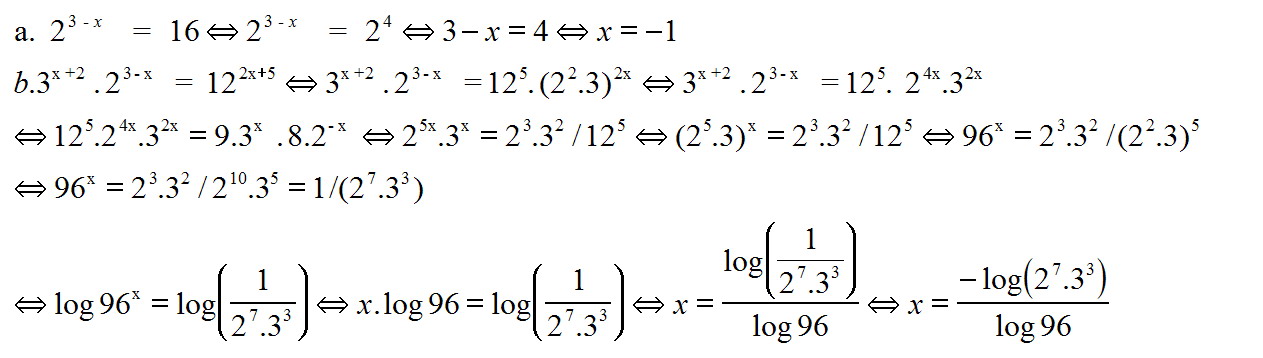
Xem  https://goo.gl/Y7gziQ
Xem  https://goo.gl/L5cGuf


Ví dụ 2. 
Giải phương trình mũ quy về đa thức  .

(i) $4^x-2=2^x$

(ii) $27^x-3^{2x+1}+2.3^x=0$

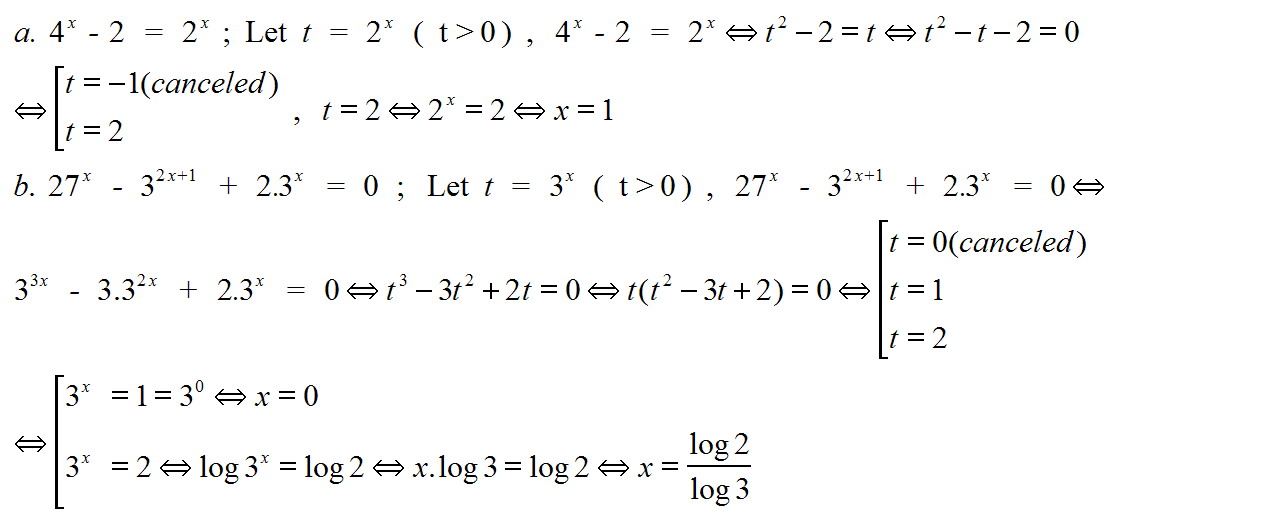
Xem  https://goo.gl/3xrmDX
Xem  https://goo.gl/oPcdWo


Ví dụ 3. 
Giải phương trình mũ cơ số tích .

(i) $5.4^x+2.25^x=7.10^x$

(ii) $3.4^x-2.6^x-9^x=0$

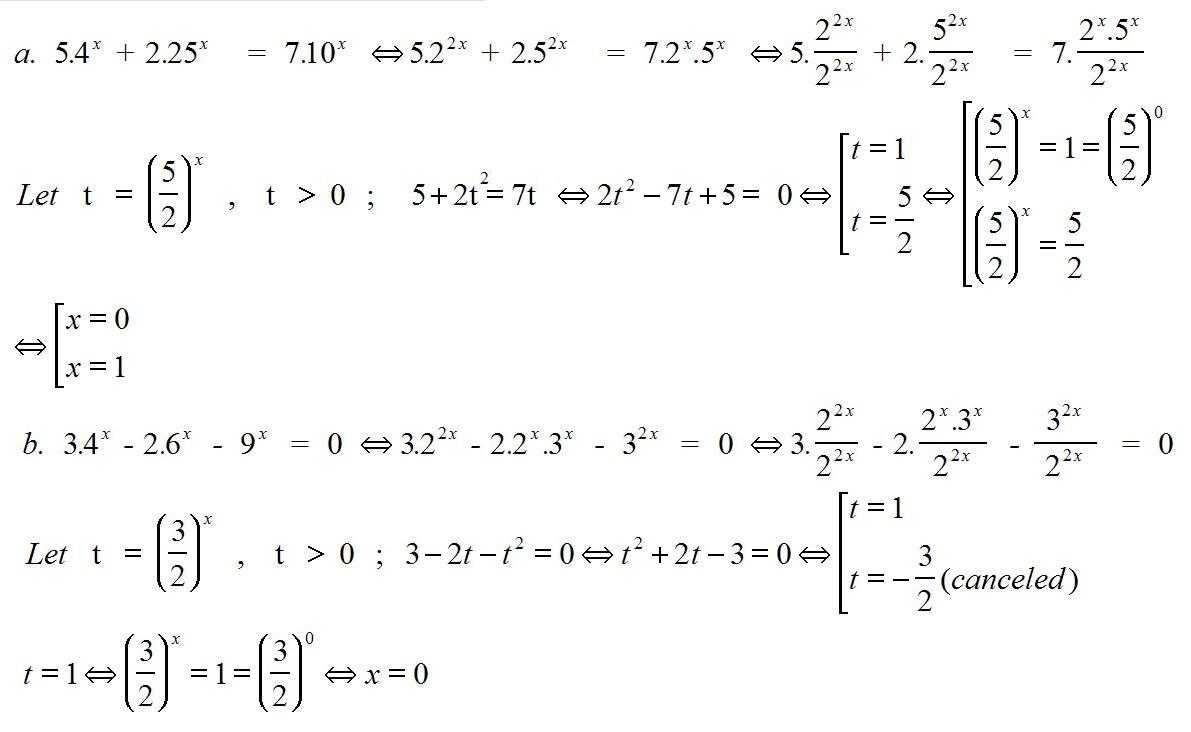
Xem  https://goo.gl/5YUYky
Xem  https://goo.gl/AFCWUh


Ví dụ 4. 
Giải phương trình mũ cơ số lượng liên hiệp .

(i) $(4+\sqrt{15})^x+(4-\sqrt{15})^x=62$

(ii) $(2+\sqrt{3})^x-2.(2-\sqrt{3})^x+1=0$




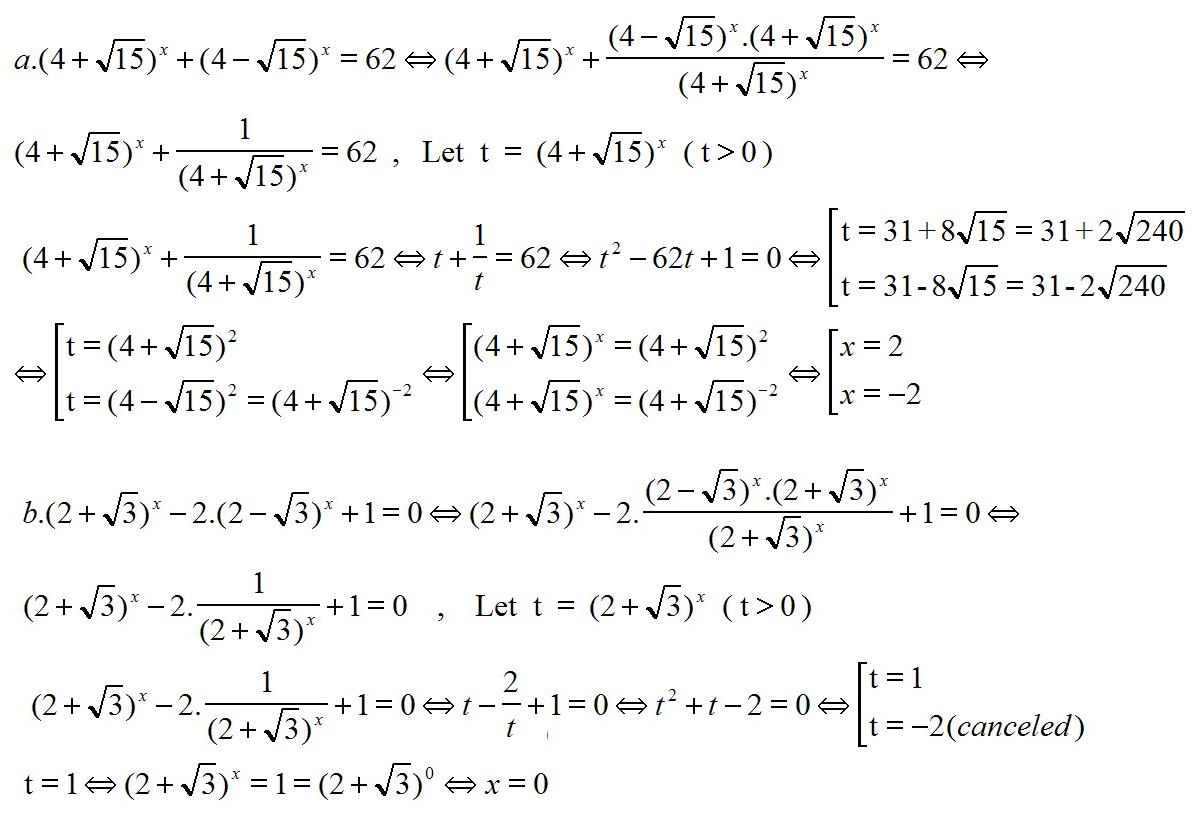
Xem  https://goo.gl/QZCnqt
Xem  https://goo.gl/u2U4QT


Ví dụ 5. 
Giải phương trình mũ 2 vế 2 cơ số khác nhau .

(i) $2^x+2^{x-1}+3^{x-1}=3^x-3^{x-2}-2^{x-2}$

(ii) $4.7^{3x}+9.5^{2x}=2.5^{2x}+9.7^{3x}$

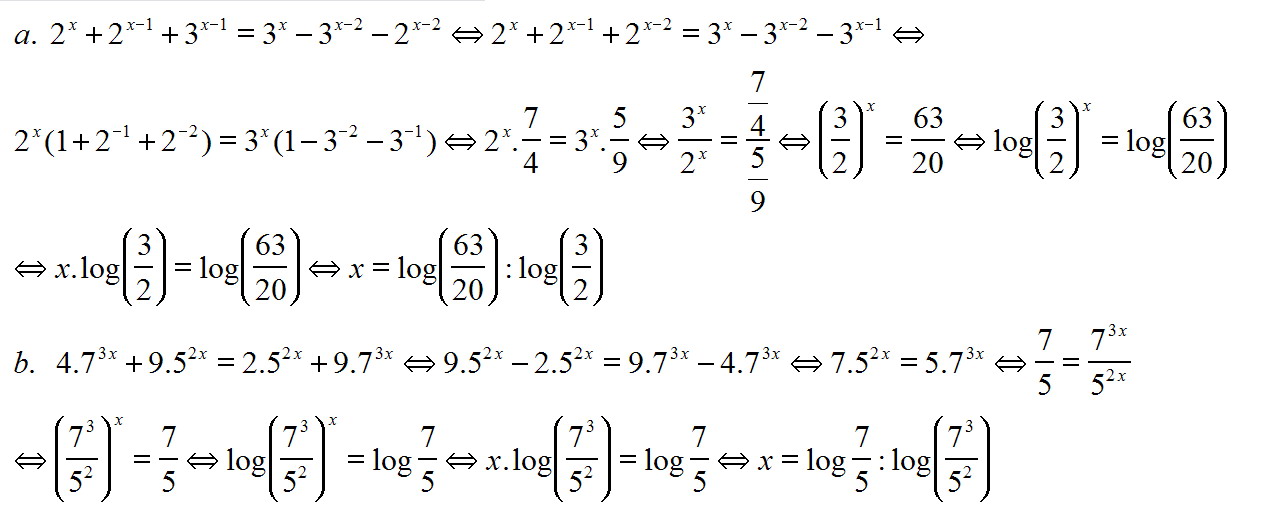
Xem  https://goo.gl/X38xDW
Xem  https://goo.gl/tCFwUM


Ví dụ 6. 
Giải phương trình mũ - logarith hóa .

(i) $3^x.8^{x/(x+1)}=36$

(ii) $5^x.8^{x/(x+1)}=100$

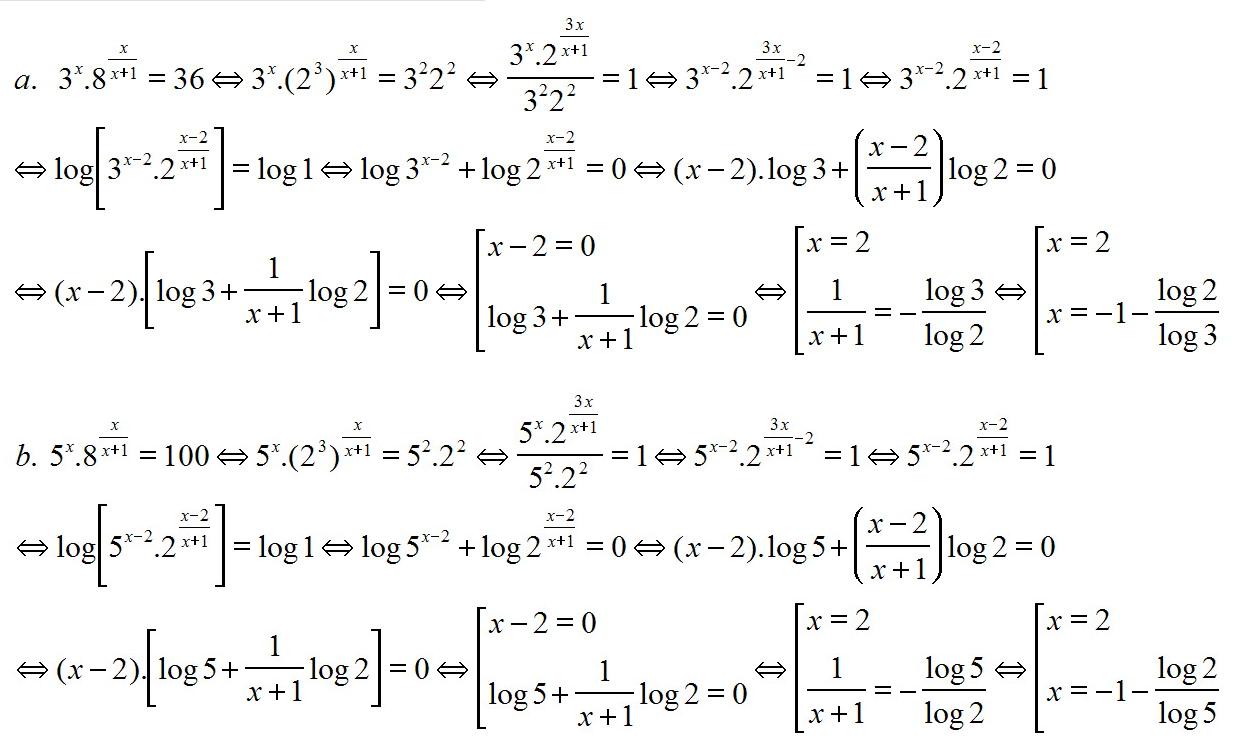
Xem  https://goo.gl/BBMtMr
Xem   https://goo.gl/Pujz1m     https://goo.gl/TdDhU7

Ví dụ 7. 

Giải phương trình mũ - đa thức .

(i) $2^x=3-x$

(ii) $2.3^x-5x=8$



Xem  https://goo.gl/j2nMHu    https://goo.gl/TdDhU7
Xem  https://goo.gl/vGBemX


Ví dụ 8. 
Giải phương trình mũ - logarith .
(i) $log_{3}(4.3^x-1)=2x+1$

(ii) $4^{log_{3}x}-5.2^{log_{3}x}+2^{log_{3}9}=0$

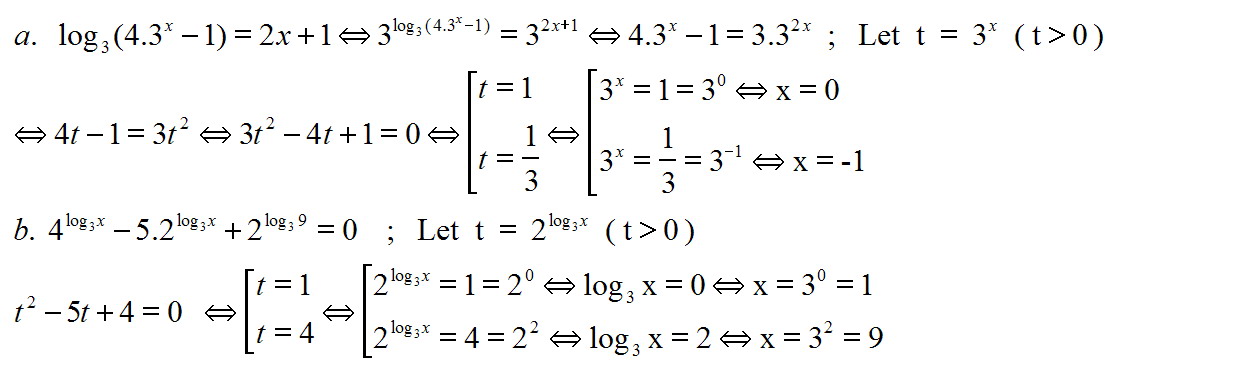
Xem  https://goo.gl/jBjea8     https://goo.gl/3YirL6

Xem  https://goo.gl/jBjea8    https://goo.gl/FkTnie


Ví dụ 9. 
Giải phương trình mũ - cơ số đảo .

(i)  $5^\sqrt{x}-5^{3-\sqrt{x}}=20$

(ii)  $3^{x^2}+3^{1-x^2}=4$

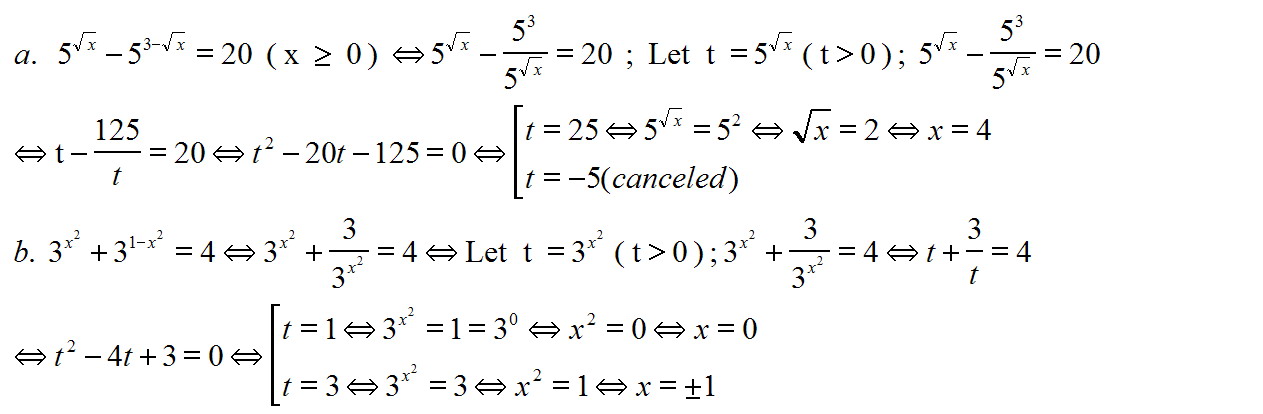
Xem  https://goo.gl/NYimwK
Xem  https://goo.gl/75FNCx


Ví dụ 10. 
Giải phương trình mũ - tích số .

(i) $ 3.8^x+4.12^x-18^x-2.27^x=0$

(ii)  $2^{x^2+x}-2^{x^2-x+2}-2^{2x}+4=0$

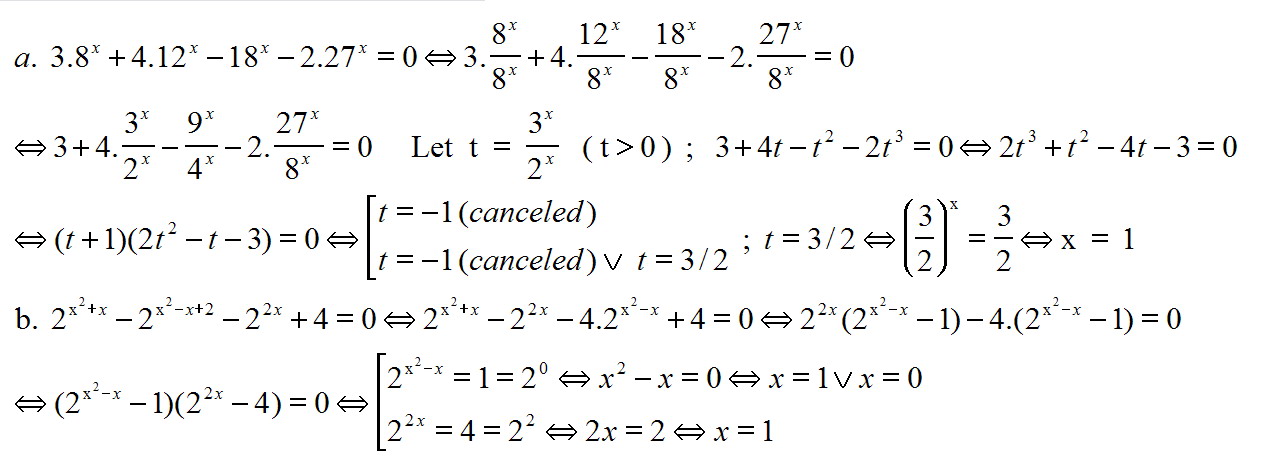
Xem  https://goo.gl/hoxXpv     https://goo.gl/4q75sr
Xem   https://goo.gl/hoxXpv     https://goo.gl/6JD3jb





Trần hồng Cơ
Ngày 29/07/2016




 ------------------------------------------------------------------------------------------- 

 Love not the world, neither the things that are in the world. If any man love the world, the love of the Father is not in him. For all that is in the world, the lust of the flesh, and the lust of the eyes, and the pride of life, is not of the Father, but is of the world. 

1 John 2:15-16 KJV 

 Chớ yêu thế gian cùng những gì trong thế gian. Nếu ai yêu thế gian thì sự kính yêu Thượng Đế không ở trong người ấy. 

 I Giăng 2:15