KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D -
Phần 4 . Co - Eq (11-21)
Lời nói đầu .
Như chúng ta đã biết loạt bài " DANH MỤC CÁC ĐƯỜNG CONG " được trình bày trước đây gồm có 3 phần . Nội dung của những phần này là liệt kê các phương trình , tên gọi cùng các giai thoại và chú thích lịch sử của một số đường cong thường xuất hiện trong toán học , vật lý , thiên văn và nhiều ngành kỹ thuật khác .
Bạn đọc có thể theo dõi chi tiết trên các trang sau :
Phiên bản mới nhất đăng trên
http://tusach.thuvienkhoahoc.com/wiki/Danh_mục_và_lịch_sử_các_đường_cong
Tiếp theo sau đây là chuyên mục " KHẢO SÁT THỰC NGHIỆM CÁC ĐƯỜNG CONG 2D " ,
Mục đích của chuỗi bài viết này là khảo sát đồ thị các đường cong bằng các công cụ trực tuyến (online) hoặc trình ứng dụng ( phần mềm offline ) .
Việc thực hành này là hết sức cần thiết và cũng mang lại nhiều kết quả lợi ích . Một mặt nó giúp chúng ta hiểu rõ hơn về các tính chất đặc trưng của các đường cong , mặt khác cũng là dịp làm quen với một số trình ứng dụng có quy mô lớn và tốc độ xử lý rất mạnh . Từ đó chúng ta có thêm kiến thức về đồ họa phục vụ cho việc nghiên cứu hoặc giải quyết những bài toán cụ thể trong phạm vi chuyên môn của mình .
Xin trân trọng giới thiệu cùng bạn đọc .
Trần hồng Cơ
Ngày 08 /05/ 2014 .
-----------------------------------------------------------------------------------------------------------------------------------
Xin chào các bạn , trong bài viết trước chúng ta đã thực hành đồ họa với các trình ứng dụng ( như GP ,GC , GX , wxM và MapleV) và các website trực tuyến ( WA , DE , SMS , FM , MT và FP ) bằng những thao tác nhập liệu khá đơn giản .
Triết gia kiêm toán học gia R. Descartes đã viết : " Làm việc gì bao giờ cũng đi từ dễ đến khó. Từ đơn giản đến phức tạp " . Mọi người chúng ta ai cũng biết rằng thực hành luôn đóng vai trò chủ yếu trong tư duy lý luận, phải xem đó là phép thử của quá trình nhận thức . Việc thực hành cũng vậy , chúng ta sẽ cùng nhau đi từ cơ bản đến nâng cao , từ đơn giản đến phức tạp .
Mục tiêu chính của tác giả trong bài viết này vẫn là khảo sát đồ họa , tuy nhiên ngoài những lệnh cơ bản dành cho việc nhập liệu là một số khái niệm bổ sung về các đường cong 2D .
- Dành cho bạn đọc muốn tìm hiểu sâu : Để nghiên cứu chi tiết các tính chất của đường cong các bạn download những tài liệu , hình ảnh minh họa từ mục lưu trữ ở phần cuối mỗi tiểu mục .
I . Vẽ đồ thị các đường cong từ Co - Eq [ 11 - 21 ] bằng trình ứng dụng .
1.1 Conchoid (đường vỏ sò Conchoid) [11]
A . Khái niệm .
Đường vỏ sò Conchoid Nicomedes và có nhiều ứng dụng vào việc giải quyết các bài toán về nhân đôi khối lập phương và chia một góc làm 3 phần.
Bài toán chia 3 một góc được giải như sau :
Dựng $ \Delta IHO$ vuông ở H với góc $\angle OIH = 3 \alpha$ . Từ I vẽ đường tròn (C) tâm I cắt tia bán kính OI tại M . Từ M ta dựng điểm N trên (C) với $\frown MN = 4 \alpha$ . Tia ON cắt tia HI tại J . Khi đó góc $\angle NIJ =\angle NJI = \alpha$ .
Chọn điểm O cố định và I chạy trên HJ , quỹ tích các điểm M và N là đường conchoid Nicomedes
Conchoid có x = b là một tiệm cận đứng và diện tích giới hạn bởi nhánh và tiệm cận là vô hạn.
Phương trình đường cong trong hệ tọa độ cực:
$r = a + b.secθ$
Với $0<b/a<1$
+Chiều dài cung
+Độ cong
$C(\theta)= \frac{a(a+3b.sec\theta-2b.sec^3\theta)}{(a^2+2ab.sec\theta+b^2sec^4\theta)^{3/2}}$
+Chu vi
+Diện tích
$S=b\sqrt{a^2-b^2}-2ab.ln(a-\sqrt{a^2-b^2})+a^2arccos(b/a)$
Các đường liên hợp
Xem http://youtu.be/frDBFJ9jMaA
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$(x − b)^2(x^2 + y^2) = a^2x^2$
(x − b)^2*(x^2 + y^2) = a^2*x^2
Phương trình đường cong trong hệ tọa độ cực:
$r = a + b.secθ$
r = a + b.sec(θ)
Chọn a = 2 ; b = 1
Khi đó
$(x − 1)^2(x^2 + y^2) = 4x^2$
(x − 1)^2*(x^2 + y^2) = 4*x^2
hoặc
$r = 2 + secθ$
r = 2+ sec(θ)
Dùng GP với nhập liệu r = 2+ sec(t)
Lưu trữ :
http://yadi.sk/d/x4gydGX0RCfQg
1.2 Conchoid of de Sluze (đường vỏ sò Conchoid Sluze) [12]
A. Khái niệm .
Đường cong Conchoid Sluze trong hệ tọa độ Descartes có dạng
$a(x-a)(x^2+y^2)=-k^2x^2$
+Trong tọa độ cực
$a(rcosθ - a) = -k^2cos^2θ $
bằng phép đối xứng trục thay x = - x khi đó
$a(-x-a)(x^2+y^2)=-k^2x^2$
hay
$a(x+a)(x^2+y^2)=k^2x^2$ (1)
+Trong hệ tọa độ cực
$a(-rcosθ - a) = -k^2cos^2θ$
hay
$a(a+rcosθ ) = k^2cos^2θ$
Từ (1) ta chọn $a = -1 , b = -k^2$ khi đó (1) thành $(x-1)(x^2+y^2)=b.x^2$
Phương trình tham số đường cong trong hệ tọa độ Descartes:
$x=cost(b.cost+sect)$
$x=sint(b.cost+sect)$
Với $b < -1$ và $t \in [-arcsec( \sqrt{-b}) , arcsec( \sqrt{-b})]$
+Độ dài cung
+Độ cong $C(t) = \frac{2b(b+4-3sec^2t)}{[b^2+4b-2b.sec^2t+sec^4t]^{3/2}}$
+Chu vi
+Diện tích vòng loop $S_{loop}=1/2.[(2-b)\sqrt{(-1-b)}+b(b+4)arcsec(\sqrt{-b})]$
Xem http://youtu.be/k1UUlG2gjrs
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$a.(x + a)(x^2 + y^2) = k^2x^2$
a*(x + a)*(x^2 + y^2) = k^2*x^2
Phương trình đường cong trong hệ tọa độ cực:
$a.(a + r.cosθ) = k^2.cos^2θ$
a*(a + r*cos(θ)) = k^2*cos(θ)^2
Chọn a = 2 ; k = 3
Khi đó
$2.(x + 2)(x^2 + y^2) = 9x^2$
2*(x + 2)*(x^2 + y^2) = 3^2*x^2
hoặc
$2.(2 + r.cosθ) = 9.cos^2θ$
2*(2 + r*cos(θ)) = 9*cos(θ)^2
giải theo r , ta có r = (9*cos(θ)^2 /2 - 2)/cos(θ)
Dùng GP với nhập liệu r = (9*cos(t)^2 /2 - 2)/cos(t)
Lưu trữ :
http://yadi.sk/d/UNobDrYkRCfXj
1.3 Cycloid (đường bánh xe cycloid) [13]
A. Khái niệm .
Xét đường tròn (C) có bán kính a = 1, trên trục Ox. Một điểm M cố định trên đường tròn đó. Khi đường tròn (C) lăn (không trượt) trên trục Ox, quỹ tích điểm M là một đường cong có tên gọi cycloid.
Như vậy có thể xem Cycloid là quỹ tích của một điểm M có khoảng cách h từ tâm của một đường tròn bán kính a lăn không trượt dọc theo một đường thẳng.
Nếu h < a nó là một cycloid curtate.
Nếu h > a nó là một cycloid prolate.
Nếu h = a nó là một cycloid .
Vài hình ảnh về cycloid tương ứng với tham số h/R
h/a ~ 4.61
h/a ~ 7.83
$ x = at - a.sint , y = a - a.cost$ từ $y = a - a.cost$ giải tìm t , thu được
$t = arccos(1- y/a)$ và $cost = 1 - y/a$ . Thế vào x , ta có $x=a.arccos(1- y/a) -a. \sqrt{1-(1 - y/a)^2}$
Rút gọn ta có
$x=a.arccos(1- y/a) - \sqrt{2ay-y^2}$
Tính diện tích giới hạn bởi cung cycloid và trục Ox với t thuộc $ [ 0,2 \pi]$ .
$ x = at - a.sint \Rightarrow x' = a - a.cost$ .
Diện tích $S=\int_{0}^{2\pi }y(t)x'(t)dt=\int_{0}^{2\pi }a^2(1-cost)^2dt$
$S= \left [ a^2(3t/2-2sint+cost.sint/2) \right ] _{t=0}^{t=2\pi}=3 \pi a^2$
Tính chiều dài của cung cycloid với t thuộc $ [ 0,2 \pi]$ .
$L=\int_{0}^{2\pi}\sqrt{{x'(t)}^2+{y'(t)}^2}dt=\int_{0}^{2\pi} a \sqrt{2-2cost}dt=2a \int_{0}^{2\pi}sin(t/2)dt$
Vậy $L=8a$
Với h = a , phương trình tham số của cycloid trong hệ tọa độ Descartes là
$ x = at - a.sint , y = a - a.cost$
+Chiều dài cung $L(t)=8a.sin^2(t /4)$
+Độ cong $C(t) = - \frac{|csc(t /2)|}{4a}$
+Chu vi $L=8a$ với $t \in [ 0,2 \pi]$
+Diện tích $S=3 \pi a^2$
Các đường liên hợp
Xem http://youtu.be/ZoI8alORhVM
B. Phương trình .
Phương trình tham số trong hệ tọa độ Descartes:
$ x = at - h.sint , y = a - h.cost$
x = a*t - h*sin(t) , y = a - h*cos(t)
chọn a = 2 , h = 1 ( đây là cycloid curtate )
Khi đó
$ x = 2t - sint , y = 2 - cost$
x = 2*t - sin(t) , y = 2 - cos(t)
Dùng GX nhập liệu x = 2*t - sin(t) , y = 2 - cos(t)
Lệnh GX như sau :
plotparam([2*t - sin(t),2 - cos(t)] , t=0..10*3.14,tstep=0.1,display=magenta+filled);
Mô hình chuyển động điểm trên cycloid
Xem http://youtu.be/xad90d1H_Wg
Lưu trữ :
http://yadi.sk/d/_xC7naDIRCw3u
1.4 Devil's curve (đường cong quỷ) [14]
A. Khái niệm .
Phương trình tổng quát của đường cong quỷ trong hệ tọa độ Descartes là
hoặc
phương trình trong tọa độ cực
+ Đồ thị gồm 2 nhánh vô cực và hình số 8 ( xuất hiện khi a < b ) xem hình động sau
Từ điểm M thuộc nhánh vô cực của đường cong quỷ , nối OM dựng $ \Delta ONH$ vuông ở H với HN = b (const ) và OM = ON , khi đó quỹ tích của H là nhánh vô cực hyperbola .
+Đường cong hình số 8 cũng được dựng từ cùng một hyperbola như trên . Khi H chạy trên hyperbola ,nối OH và dựng $ \Delta OMH$ vuông ở O , cạnh huyền HM = b (const) , khi đó điểm M chạy trên đường cong hình số 8 .
+Để ý rằng khi b = 0 từ phương trình tổng quát ta sẽ có trường hợp đặc biệt là một hyperbol $x^2-y^2=-a^2$ . Khi a = 25/24 đường cong có tên là đường cong động cơ điện.
Phần giữa đường cong giống như các cuộn dây đồng , được xoay do tác dụng lực từ của các nam châm xung quanh.
Các đường liên hợp
Xem http://youtu.be/fMdA5ngp6Fc
B. Phương trình .
Bằng cách đặt $B = a^2 - b^2 ; A=a^2 + b^2$ thay vào dạng tổng quát
Phương trình đường cong trong hệ tọa độ Descartes :
$ Bx^2 + Ay^2 = x^4 − y^4$
B*x^2 + A*y^2 = x^4 − y^4
Chọn B = 25/24 và A = -1
Khi đó : $ 25x^2/24 - y^2 = x^4 − y^4$
(25/24)*x^2 - y^2 = x^4 − y^4
Dùng GX với nhập liệu dạng ẩn (25/24)*x^2 - y^2 = x^4 − y^4
Phương trình đường cong trong hệ tọa độ cực:
$r = \sqrt{(25-24tan^2θ)/(1-tan^2θ)}$
r = sqrt((25-24tan(θ)^2)/(1-tan(θ)^2))
Dùng GP với nhập liệu r = sqrt((25-24*tan(t)^2)/(1-tan(t)^2))
Lưu trữ :
http://yadi.sk/d/4LTxEJstRCfDo
1.5 Double Folium (đường cong lá đôi) [15]
A. Khái niệm .
Phương trình tổng quát đường hình lá được cho bởi công thức $(x^2 + y^2)(x^2 + bx + y^2) = 4axy^2$
hoặc, trong tọa độ cựclà : $ r = − bcosθ + 4acosθsin^2θ$
Tên gọi Folium có nghĩa là hình lá. Có nhiều dạng đường cong nhưng ba dạng đặc biệt là đường lá đơn, lá đôi và lá ba, tương ứng với b = 4a, b = 0, b = a ( xem hình )
Các bifolium có thể được xây dựng như sau.
Cho đường tròn (C) qua gốc tọa độ O, điểm A (0, a) và B (1, 0), và đường thẳng m qua O cắt (C) tại Q. Gọi R là hình chiếu của Q trên trục x và P là hình chiếu của Q trên m.
Đường cong bifolium là tập hợp các điểm P, khi m thay đổi và điểm Q chạy trên đường tròn C cho trước .
+ Với $ a\geq 1 $ đồ thị có dạng lá đơn ( single folium ) .
+ Với $ a = 0 $ đồ thị có dạng lá đôi ( double folium hay bifolium ) .
Khi a = 1/2 đường lá ba còn có tên là trefoil, đường cong torpedo hay siluroid như sau
Phương trình tham số của đường cong trong hệ tọa độ Descartes
$x = 4a.sin^2t.cos^2 t, y = 4a.sin^3t.cost$
+Chiều dài cung $L(x) = 1/42 .a.[ 35[E(\phi,k)+E(k)]x+4\sqrt{2}.[(7F(\phi,k)+K(k))x + 2.x'^2]]$
Với $\phi =arcsin[ 1/7. ( 9 - 4\sqrt{2})]$ hay $\phi \approx 0.497$
$k = \sqrt{-1/7. \sqrt{ 57 + 40 \sqrt{2}}}$ hay $k \approx 4.027i $
Trong đó $E(\phi,k) , F(\phi,k) , E(k) , K(k)$ là các tích phân Elliptic .
Các bạn xem chi tiết tại
HÀM ĐẶC BIỆT - Phần 2 .
http://tinyurl.com/k6gmpho
Phương trình đường cong trong hệ tọa độ cực:
$ r = 4acosθ.sin^2θ$
+Độ cong $C(\theta) = \frac{(cos4\theta+3cos2\theta+3)csc\theta}{a. \sqrt{2}(2cos4\theta+3cos2\theta+3)^{3/2}}$
+Chu vi $P \approx 7.155a$
+Diện tích $S = \pi a^2 /2$
Các đường liên hợp
Xem http://youtu.be/TyFeBu0J3uo
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$(x^2 + y^2)^2 = 4axy^2$
(x^2 + y^2)^2 = 4*a*x*y^2
Phương trình đường cong trong hệ tọa độ cực:
$ r = 4acosθ.sin^2θ$
r = 4*a*cos(θ).sin(θ)^2
Dùng GP với nhập liệu với r = 4*a*cos(t).sin(t)^2 với các trị số của a .
Lưu trữ :
http://yadi.sk/d/GfTubevbRCj7m
1.6. Durer's shell curve (đường vỏ sò Durer) [16]
A. Khái niệm .
Trong mặt phẳng Oxy lấy hai điểm Q (q, 0) và R (0, r) sao cho q + r = a . Dựng điểm P trên đường thẳng RQ thỏa PQ = b . Quỹ tích các điểm P xác định đường vỏ sò Dürer .
Bỏ qua các phép biến đổi tuyến tính, hình dạng của đường cong chỉ phụ thuộc vào tỷ số b / a, và có thể được thay thế bằng một tham số.
Định nghĩa của đường cong này là một biến thể của một conchoid (bình thường) .
Đôi khi họ các đường conchoid biến thể này được gọi là đường vỏ sò Dürer .
Các đường cong xuất hiện trong tác phẩm 'Hướng dẫn đo đạc bằng compa và thước kẻ ' của Albrecht Dürer (1471 - 1528),(1525). Tuy nhiên Dürer chỉ tìm thấy một trong hai nhánh của đường cong , ông đặt tên là đường cong 'ein muschellini' ( vỏ sò ). Dürer đã chọn a = 13, với các điểm P và P ' ta có PRQ - RQP' = 16 .
Một số dạng biểu diễn phương trình đường vỏ sò Durer như sau
, 
, 
Hay
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$(x^2 + xy + ax − b^2)^2 = (b^2 − x^2)(x − y + a)^2$
(x^2 + x*y + a*x - b^2)^2 = (b^2 - x^2)*(x - y + a)^2
+Khi $b = 0$ đường cong Durer suy biến thành $x^2 = 0$
+Khi $a = 0$ đường cong Durer suy biến thành cặp đường thẳng $x = b/ \sqrt{2} , x = -b/ \sqrt{2}$ cùng với đường tròn $x^2+y^2=b^2$
+Khi $a = b/2 $ đường cong Durer có đỉnh tại $S(-2a,a)$ .
Dùng GX với nhập liệu (x^2 + x*y + a*x - b^2)^2 = (b^2 - x^2)*(x - y + a)^2
với { a = 1 , b = 0 } , { a = 0 , b = 1 } , { a = 1 , b = 2 } ta có các đồ thị đặc biệt .
Lưu trữ :
http://yadi.sk/d/TZcDbJrbRCZqT
1.7 Figure Eight Curve (đường cong hình số 8) [17]
A. Khái niệm .
Đường cong hình số 8 còn được gọi là Lemniscate của Gerono .
Cho đường tròn (C) bán kính bằng 1 tâm ở gốc O. P là một điểm chạy trên đường tròn (C) . Gọi M là giao điểm của đường thẳng x = 1 và đường thẳng nằm ngang đi qua P và Q là giao điểm của OM và đường thẳng đứng qua P. Khi P di chuyển trên đường tròn thì qũy tích của Q là đường cong hình số 8.
+Đường cong hình số 8 là dạng đặc biệt của Hippopede có nghĩa đen là đường "chân ngựa" .
Các đường cong dạng này cũng được J. Booth (1810-1878) nghiên cứu , nên còn có tên gọi là đường cong Booth.
Phương trình đường cong Hippopede trong hệ tọa độ cực là
$ r^2 = 1 - a.sin\theta$ về hình thức có ba dạng :
Với a < 1/2 : một hình bầu dục
Với 1/2 < a <1: một hình bầu dục lõm
Với a > 1: đường cong hình số 8
Đối với a < 1, đường cong là hình bầu dục Booth.
Cho a > 1, đường cong là lemniscate Booth.
Khi tham số a = 2, đường cong là lemniscate của Bernoulli . Trong hình động dưới đây ta chọn a = 2 .
Chú thích lịch sử :
Proclus (75 TCN) và Eudoxus là những người đầu tiên khảo sát các đường cong Hippopede .
Sau thời Proclus đường cong này đã được đặt tên Hippopede Proclus để ghi nhớ công trình nghiên cứu của ông .
Đường cong hình số 8 cũng là dạng đặc biệt của họ đường cong besace . Về bản chất besace là một đường cong Lissajous. Năm 1750 Cramer đã đặt tên chính thức cho đường cong này là Quersackkurve . Phương trình besace có dạng :
$(y+ax^2)^2=x^2-x^4$
Khi a lớn, đường cong xấp xỉ với parabol.
Khi a = 0 đường cong là lemniscate Gerono:
$y^2 = x^2 - x^4$
Đường cong cũng có hình dạng của một ruy băng như lemniscate Bernoulli.
Phương trình tham số đường cong trong hệ tọa độ Descartes :
$x=a.sint $
$y=a.sintcost$
+Chiều dài cung
+Độ cong $C(t)= \frac{-2 \sqrt{2}(cos2t+2).sint}{a[cos4t+cos2t+2]^{3/2}}$
+Chu vi $P=a.[2^{9/4}(E(k)-K(k))+(3+2 \sqrt{2}).2^{-1/4}.\Pi((4-3\sqrt{2})/8,k)]$ với $k = \sqrt{2^{-1/2}+2^{-2}}$
hay $P \approx 6.097a$
+Diện tích $S=4a^2/3$
Một mô hình cơ học minh họa điểm chuyển động theo quỹ đạo hình số 8 .
Xem http://youtu.be/S-vqRfyoIyo
Phương trình đường cong trong hệ tọa độ Descartes :
$x^4 = a^2(x^2 − y^2)$
x^4 = a^2*(x^2 − y^2)
Phương trình đường cong trong hệ tọa độ cực:
$r^2 = a^2.cos2θ.sec^4θ$
r^2 = a^2.cos(2*θ).sec(θ)^4
Dùng GP với nhập liệu r = sqrt(a^2*cos(2*t)*sec(t)^4) và r = - sqrt(a^2*cos(2*t)*sec(t)^4)
Lưu trữ :
http://yadi.sk/d/dPaZVUboRCZn4
1.8 Ellipse (đường Ellipse) [18]
A. Khái niệm .
Ellipse là trường hợp đặc biệt khi nghiên cứu về giao tuyến của hình nón và mặt phẳng , gọi chung là conic .
Chu vi của ellipse có công thức gần đúng là $C = \pi [3(a+b) - \sqrt{(a+3b)(3a+b)}]$ . Vài cách dựng hình ellipse
+ Thước và dây :
Phương trình tham số trong hệ tọa độ Descartes:
$x = acost , y = bsint$
+Chiều dài cung $L(t)=aE(t,e)$ với $e=\sqrt{1-b^2/a^2}$
+Độ cong $C(t) = ab/(a^2sin^2t+b^2cos^2t)^{3/2}$
+Chu vi $P=4aE(e)$ hay $P \approx \pi \sqrt{2(a^2+b^2)}$
+Diện tích $S= \pi a b$
Các đường liên hợp
Xem http://youtu.be/-6axJSSpqMg
B. Phương trình .
Phương trình đường cong trong hệ tọa độ Descartes:
$ x^2/a^2 + y^2/b^2 = 1$
x^2/a^2 + y^2/b^2 = 1
Phương trình đường cong trong hệ tọa độ cực :
$r=\frac{a(1-e^2}{1=e.cos\theta}$
Phương trình tham số trong hệ tọa độ Descartes:
$x = acost , y = bsint$
x = a*cos(t) , y = b*sin(t)
Lưu trữ :
http://yadi.sk/d/jio_Ew2yRCnTG
1.9 Epicycloid (đường Epicycloid) [19]
A. Khái niệm .
Một họ gồm bốn đường cong liên quan đến Epicycloid là Epicycloid, Epitrochoid, Hypocycloid và Hypotrochoid là quỹ tích một điểm P trên chu vi đường tròn bán kính b lăn không trượt trên đường tròn bán kính a cố định. Đối với Epicycloid thì đường tròn bán kính b lăn bên ngoài đường tròn bán kính a.
Trường hợp đặc biệt $a = b$ epicycloid biến đổi thành cardioid.
Nếu $a = 2b$ epicycloid biến đổi thành nephroid.
Nếu $a = (m - 1) b $ với m là một số nguyên, chu vi của epicycloid là $8bm$ và diện tích của nó là $πb^2(m^2 + m)$
+Độ cong $C(t) = \frac {a+2b}{4b(a+b)sin(\frac{at}{2b})}$
+Chu vi $P=8(ab+b^2)/a$
+Diện tích giới hạn giữa epicycloid và tiếp tuyến $S= \pi b(a+b)(a+2b)/a$
+Phương trình tiếp tuyến tại điểm $M(t)$
$x.sin(\frac{a}{2b}+1)t - y.cos(\frac{a}{2b}+1)t - a .( 1 + 2b/a)sin(\frac{at}{2b})=0$
Các đường liên hợp
Xem http://youtu.be/ccziVJC45OE
B. Phương trình .
Phương trình tham số trong hệ tọa độ Descartes:
$x = (a+b)cost - b.cos(a/b+1)t$
$y = (a+b)sint - b.sin(a/b+1)t$
x = (a+b)*cos(t) - b*cos(a/b+1)*t
y = (a+b)*sin(t) - b*sin(a/b+1)*t
Phương trình đưởng cong chuyển từ dạng tham số trong hệ tọa độ Descartes sang hệ tọa độ cực
$r^2 = (a+b)^2 + b^2 -2b(a+b)cos(at/b)$
r^2 = (a+b)^2 + b^2 -2*b*(a+b)*cos(a*t/b)
Khi $a = nb$ ( đường tròn b lăn n vòng ) ta có epicycloid n đỉnh , khi đó phương trình đường cong là :
$r^2 = a^2[(n+1)^2-2(n+1)cos(nt)+1]/n^2$
Dùng GP với nhập liệu r =sqrt( (a+b)^2 + b^2 -2*b*(a+b)*cos(a*t/b))
Ví dụ với a = 2 , b = 1 ta có r =sqrt( 10 - 6*cos(2*t)) đồ thị là nephroid .
Thực hành :
r =sqrt(5-6cos(t)) [1 đỉnh ]
r =sqrt( 10 - 6*cos(2*t)) [2 đỉnh ]
r =sqrt( 17 -8*cos(3*t)) [3 đỉnh ]
r =sqrt( 26 -10*cos(4*t)) [4 đỉnh ]
r =sqrt( 37 -12*cos(5t)) [5 đỉnh ]
Xem hình động :
Lưu trữ :
http://yadi.sk/d/x1qlLMOxRCrLX
2.0 Epitrochoid (đường Epitrochoid) [20]
A. Khái niệm .
Epitrochoid là quỹ tích điểm P trên một đường tròn bán kính b lăn không trượt trên một đường tròn bán kính a cố định . P là điểm có khoảng cách c tính từ tâm của đường tròn bán kính b . Epitrochoid có liên quan với Epicycloid , Hypocycloid và Hypotrochoid
Trong hình minh họa dưới đây h = c là khoảng cách từ P đến tâm đường tròn bán kính b . Hai trường hợp của Epitrochoid tương ứng với h = c < b và h = c > b
-Khi a = b epitrochoid biến thành limacon .
Ví dụ : a = b = 3 ; c = 4 [ Limacon ]
x = 6*cos(t) - 0.5*cos(2*t)
y = 6*sin(t) - 0.5*sin(2*t)
-Khi a = 0 epitrochoid biến thành đường tròn .
Ví dụ : a = 0 , b = 3 , c =4 [ Đường tròn ]
x = 3*cos(t) - 4*cos(t)
y = 3*sin(t) - 4*sin(t)
-Khi h = c = b epitrochoid biến thành epicycloid .
Ví dụ : a = 8 ; b = c = 4 [ epicycloid ]
x = 12*cos(t) - 4*cos(3*t)
y = 12*sin(t) - 4*sin(3*t)
+Chiều dài cung
+Độ cong
$C(t) = b^3.[h^2(a+b)+b.(b^2-2bh.cos\frac{at}{b}-ah.cos\frac{at}{b})]/(a+b)^4/[b^2-2bh.cos\frac{at}{b}+h^2]^{3/2}$
+Chu vi
+Diện tích
Các đường liên hợp
Xem http://youtu.be/lJbaL9-PYr4
B. Phương trình .
Phương trình tham số trong hệ tọa độ Descartes:
$x = (a+b)cost - c.cos(a/b+1)t$
$y = (a+b).sint - c.sin(a/b+1)t$
x = (a+b)*cos(t) - c*cos(a/b+1)*t
y = (a+b)*sin(t) - c*sin(a/b+1)*t
Lưu trữ :
http://yadi.sk/d/xBM6M-3qRCea3
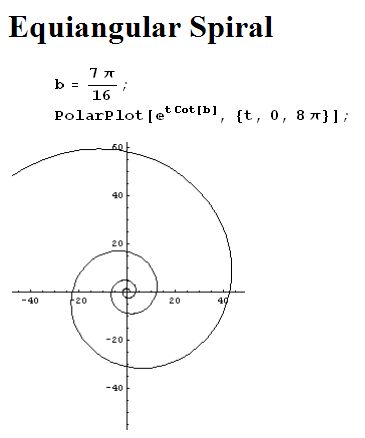
2.1 Equiangular Spiral (đường xoắn ốc đẳng giác) [21]
A. Khái niệm .
Đường xoắn ốc đẳng giác tạo ra một góc không đổi b với bất kỳ vector bán kính nào .
Xem chi tiết : http://www.geogebratube.org/student/m14470
Trong trường hợp đặc biệt, khi b = π / 2 đường xoắn ốc biến thành đường tròn.
Đối với các đường cong được hiển thị ở trên thì b = 7π/16.
P là điểm bất kỳ trên đường xoắn ốc thì chiều dài của đường xoắn ốc từ P đến tâm đường cong là hữu hạn . Khoảng cách từ P đến cực là d.sec(b) với d là khoảng cách của vector bán kính OP. Chiều dài của đường cong từ một điểm ở khoảng cách d tính từ điểm gốc cùng một vector bán kính khoảng 5,126 d.
http://www.geogebratube.org/material/show/id/47179
Vài tính chất cần nhớ :
$r = a.e^{kθ} ; k = cotb$
b là góc hợp bởi tia bán kính và tiếp tuyến tại 1 điểm trên đường cong .
Tọa độ cong $s = r/cosb$
Bán kính cong $R_{c} = r / sinb = s.cotb$
+Chiều dài cung $L(\theta) = a.e^{kθ}/cosb$
+Độ cong $C(\theta)= 1/a . e^{-kθ}.sin\theta$
+Chu vi
+Diện tích
Các đường liên hợp
Xem http://youtu.be/bsOk8eL3RXY
B. Phương trình .
Phương trình đường cong trong hệ tọa độ cực:
$r = a.e^{θ.cotb}$
r = a.e^(θ*cot(b))
Dùng GP với nhập liệu r = 0.5*e^(t*cot(7*Pi/16)) ( xem hình )
plotpolar(0.5*e^(t*cot(7*Pi/16)),t=0..30.14,tstep=0.1,display=blue+filled,thickness=2)
Lưu trữ :
http://yadi.sk/d/e2oDaW0yRCjM5
II . Các lệnh đồ họa trong trình ứng dụng Maple .
Maple V là phiên
bản cũ ( tuy vậy cũng còn khá tốt khi vẽ đồ thị và đặc biệt là miễn phí ) chưa
có nhiều tính năng đồ họa nên phần tiếp sau đây tác giả sẽ trình bày tóm lược
cách vẽ dồ thị các hàm số với các cấu trúc cơ bản . Bạn đọc có thể tìm hiểu
thêm những nội dung khác trong phần Help của phần mềm này để biết thêm các chi tiết
.
2.1 Đồ thị 2D .
2.1.1. Hàm
thông thường y = f(x) .
a. Cấu trúc lệnh
. > plot([expr1,expr2],x=xmin..xmax,y=ymin..ymax,options);
Ví dụ . Vẽ các hàm f(x) = x*sin(x) và g(x) = sin(x)/x
>
f:=x*sin(x);g:=sin(x)/x;
> plot(f,x=0..4*Pi);
> plot(g,x=0.1..4*Pi,color=blue);
> plot([f,g],x=0.1..4*Pi,color=[red,blue],
thickness=2);
Để vẽ hàm trong tọa
độ cực , ta thêm tùy chọn coords = polar .
Ví dụ . > plot(g,x=0.1..4*Pi,coords=polar,color=green
, thickness=2);
Khi click trái
vào điểm trên đồ thị , tọa độ sẽ hiển thị trên thanh công cụ . Click phải lên đồ
thị sẽ cho các tùy chọn thay đổi như style , axes , projection .
b. Giới hạn và
mở rộng khoảng giá trị đồ thị - Màu sắc – Trục .
Ví dụ . vẽ hàm số f(x) = 3*sin(x)*cos(2*x)-sin(2*x)
trên khoảng giá trị [ 1 , 4 ] ;
>plot(3*sin(x)*cos(2*x)-sin(2*x),x=-2*Pi..2*Pi,
y=1..4,color=cyan);
Ví dụ . vẽ hàm số f(x) = sin(x)/x khi x → ¥
> plot((x+1)/(x^2-x+1),x=0..infinity);
+Các tùy chọn về
màu sắc .
aquamarine , black, blue, coral
, cyan , brown , gold , green , gray , grey khaki , magenta , maroon , navy , orange ,
pink , plum , red , sienna , tan , turquoise , violet , wheat , white , yellow .
+Các tùy chọn về
trục và tựa đề .
Trục :
axes = { box , frame , none ,
normal }
Tên trục : labels
= [ ` ` , `
` ]
Tựa đề :
title = ` `
c . Các tùy chọn
về hệ trục tọa độ và phép đổi trục 2D .
bipolar, cardiod ,
cassinian , elliptic, hyperbolic, invcassinian, invelliptic, logarithmic,
logcosh , maxwell, parabolic, polar, rose, tangent .
+Phép biến đổi từ
hệ trục khác về hệ trục Descartes 2D như sau .
(u, v) → (x, y)
+ Các hệ trục .
bipolar: ( phép biến đổi Spiegel )
x = sinh(v)/(cosh(v)-cos(u))
y = sin(u)/(cosh(v)-cos(u))
cardiod:
x = 1/2*(u^2-v^2)/(u^2+v^2)^2
y = u*v/(u^2+v^2)^2
cartesian:
x = u
y = v
cassinian: (Cassinian-oval)
x =
a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) +
exp(u)*cos(v)+1)^(1/2)
y =
a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) -
exp(u)*cos(v)-1)^(1/2)]
elliptic:
x = cosh(u)*cos(v)
y = sinh(u)*sin(v)
hyperbolic:
x = ((u^2+v^2)^(1/2)+u)^(1/2)
y = ((u^2+v^2)^(1/2)-u)^(1/2)
invcassinian: (phép biến đổi ngược
Cassinian-oval)
x =
a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) +
exp(u)*cos(v)+1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)
y =
a*2^(1/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) -
exp(u)*cos(v)-1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(1/2)
invelliptic: (phép biến đổi ngược elliptic)
x = a*cosh(u)*cos(v)/(cosh(u)^2-sin(v)^2)
y = a*sinh(u)*sin(v)/(cosh(u)^2-sin(v)^2)
logarithmic:
x = a/Pi*ln(u^2+v^2)
y = 2*a/Pi*arctan(v/u)
logcosh: (ln cosh)
x = a/Pi*ln(cosh(u)^2-sin(v)^2)
y = 2*a/Pi*arctan(tanh(u)*tan(v))
maxwell:
x = a/Pi*(u+1+exp(u)*cos(v))
y = a/Pi*(v+exp(u)*sin(v))
parabolic:
x = (u^2-v^2)/2
y = u*v
polar:
x = u*cos(v)
y = u*sin(v)
rose:
x =
((u^2+v^2)^(1/2)+u)^(1/2)/(u^2+v^2)^(1/2)
y =
((u^2+v^2)^(1/2)-u)^(1/2)/(u^2+v^2)^(1/2)
tangent:
x = u/(u^2+v^2)
y = v/(u^2+v^2)
Ví dụ . Đồ thị của hàm số g(x) = sin(x)/x trong các hệ trục bipolar , parabolic , elliptic và maxwell có dạng như sau
+Có thể dùng lệnh
polarplot ( ) để vẽ hàm số trong hệ tọa
độ cực
Ví dụ . Vẽ đồ thị
đường xoắn ốc đẳng giác ( Equiangular Spiral hay Logarithmic Spiral )
> polarplot(sin(theta)/theta,theta=0..8*Pi,scaling=constrained);
+Kết hợp vẽ nhiều
hàm trong hệ tọa độ cực
Ví dụ .
> S :=
t->100/(100+(t-Pi/2)^8): R := t -> S(t)*(2-sin(7*t)-cos(30*t)/2):
> polarplot([S,t->t,-Pi/2..3/2*Pi],numpoints=2000,axes=frame,color=coral);
> polarplot([R,t->t,-Pi/2..3/2*Pi],numpoints=2000,axes=NONE);
2.1.2. Hàm tham
số { x = x(t) , y = y(t) } .
a. Cấu trúc lệnh
.
> plot([x(t),y(t),t=tmin..tmax],options);
Ví dụ . Vẽ các
hàm {x(t) = sin(t)^3 và y(t) = cos(t)^3 } ,
{ x(t) = 3*(2*cos(t)-cos(2*t)) , y(t) = 3*(2*sin(t)-sin(2*t))}
> plot([sin(t)^3,cos(t)^3,t=0..2*Pi],scaling=constrained,title
= `astroid`,color=blue);
> plot([3*(2*cos(t)-cos(2*t)) ,3*(2*sin(t)-sin(2*t)) ,t=0..2*Pi],scaling=constrained,title
= `cardioid`,color= magenta);
Chúng ta có thể vẽ
nhiều hàm tham số trên cùng hệ trục tọa độ .
Ví dụ .
Vẽ đường tròn và
ellipse trong hệ tọa độ Descartes và tọa độ cực .
> plot([[2*cos(t),sin(t),t=0..2*Pi],[sin(t),cos(t),t=0..2*Pi]],scaling=constrained,color=[green,red]);
>plot([[2*cos(t),sin(t),t=0..2*Pi],[sin(t),cos(t),t=0..2*Pi]],scaling=constrained,color=[green,red],
coords=polar,title=`polar`);
b. Dùng lệnh
polarplot vẽ hàm tham số .
Cũng có thể dùng
lệnh polarplot để vẽ hàm tham số trong tọa độ cực .
Ví dụ . vẽ hàm
{ r(t) = cos(t) , θ(t) = sin(3*t)^2 }
> polarplot([cos(t),sin(3*t)^2,t=0..2*Pi]);
Vẽ đường cong lá
4 trong tọa độ cực .
>polarplot([sin(t)*cos(t)^2,sin(t)^2*cos(t),t=0..2*Pi],title=`quatrifolium-polar`,color=blue,thickness=2);
Xem thêm tài liệu về Maple .
III . Lời kết .
Đến đây chúng ta đã đi được một phần ba con đường tìm hiểu thực nghiệm các đường cong 2D . Trong bài viết sau công việc tiếp tục của chúng ta vẫn là khảo sát tính chất cơ bản và minh họa các đường cong bằng các trình ứng dụng hoặc các công cụ trực tuyến đã đề cập đến trong các bài viết trước. Tuy nhiên từ các dữ liệu lưu trữ , chúng ta sẽ bắt tay vào sử dụng các phần mềm thực hành tính toán một số bài toán đơn giản có liên quan đến các đường cong . Tác giả hy vọng rằng nội dung của bài viết này có thể đáp ứng phần nào nhu cầu nghiên cứu ứng dụng của các bạn và mong nhận được những phản hồi tích cực . Cám ơn các bạn đã theo dõi , hẹn gặp lại .
Trần hồng Cơ
Ngày 15 /05/ 2014 .
-------------------------------------------------------------------------------------------
Khoa học là một điều tuyệt vời khi không phải dùng nó để kiếm sống.
Albert Einstein .
với 
quỹ tích H là đường bicorn
] là một hằng số. Hình dạng của đường cong phụ thuộc vào tỷ số c / a
