GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN . Phần 13e . XỬ LÝ DỮ LIỆU - Phân phối chuẩn .

GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN .

Phần 13e . XỬ LÝ DỮ LIỆU  - Phân phối chuẩn .   

DANH MỤC CÔNG CỤ GIẢI TOÁN TRỰC TUYẾN  MATHEMATICA  WOLFRAM | ALPHA .

Giới thiệu .

Bạn đọc truy cập vào đường dẫn  http://cohtrantmed.yolasite.com/widgets-tructuyen  để sử dụng các widgets giải toán trực tuyến W|A Mathematica theo chỉ mục trong danh sách dưới đây .

Những widgets này đã được tác giả sắp xếp theo từng môn học và cấp lớp theo ký hiệu như sau :

D : Đại số . Ví dụ  D8.1 widget dùng cho Đại số lớp 8 , mục 1 - Khai triển , rút gọn biểu thức đại số .
H : Hình học . Ví dụ  H12.3  widget dùng cho Hình học lớp 12 , mục 3 - Viết phương trình tham số của đường thẳng trong không gian .
G : Giải tích . Ví dụ : G11.7  widget dùng cho Giải tích lớp 11 , mục 7 - Tính đạo hàm cấp cao của hàm số
GI : Giải tích cao cấp I . Ví dụ GI.15  widget dùng cho Giải tích cao cấp I , mục 15 - Khai triển hàm số bằng đa thức TAYLOR
GII : Giải tích cao cấp II .


++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


 ĐẠI SỐ 8

D8.1  Khai triển , rút gọn biểu thức đại số
D8.2  Rút gọn phân thức
D8.3  Phân tích thừa số
D8.4  Nhân 2 đa thức
D8.5  Khai triển tích số ( có thể dùng để khai triển Newton )
D8.6  Phân tích thừa số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 10

D10.1 Giải phương trình nguyên Diophante
D10.2 Giải phương trình tuyệt đối
D10.3 Giải phương trình chứa tham số
D10.4  Giải phương trình đại số
D10.5  Giải phương trình từng bước
D10.6  Giải bất phương trình minh hoạ bằng đồ thị

D10.8  Tính giá trị biểu thức hàm số
D10.9  Giải bất phương trình đại số và minh hoạ bằng đồ thị
D10.10  Giải bất phương trình đại số - tìm miền nghiệm
D10.11  Giải phương trình đại số
D10.12  Giải phương trình vô tỷ
D10.13  Giải phương trình minh hoạ từng bước
D10.14  Giải phương trình dạng hàm ẩn
D10.15  Giải hệ thống phương trình tuyến tính , phi tuyến
D10.16  Giải hệ phương trình
D10.17  Vẽ miền nghiệm của bất phương trình đại số
D10.19  Tối ưu hoá hàm 2 biến với các ràng buộc
D10.20  Tìm giao điểm của đồ thị hàm số và trục hoành Ox , trục tung Oy

HÌNH HỌC 10

H10.1  Tính diện tích tam giác trong hệ toạ độ Oxy
H10.3  Khảo sát conic ( đường tròn , Ellipse , Parabola , Hyperbola )
H10.2  Tính khoảng cách từ 1 điểm đến đường thẳng trong Oxy



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 11

D11.1 Thuật chia Euclide dùng cho số và đa thức  ( HORNER )
D11.2  Tính tổng nghịch đảo của n số tự nhiên




D11.6  Khai triển nhị thức Newton


GIẢI TÍCH 11


G11.1  Tính gíá trị một chuỗi số  theo n
G11.2  Đa thức truy hồi
G11.3  Khảo sát tính hội tụ của chuỗi số
G11.4  Tính giới hạn của chuỗi số khi  $n \rightarrow  \infty$
G11.5  Tìm hàm số ngược của hàm số cho trước
G11.6  Tìm đạo hàm của hàm số hợp - giải thích
G11.7   Tính đạo hàm cấp cao của hàm số
G11.8   Tìm giới hạn của hàm số
G11.9   Tìm giới hạn của hàm số
G11.10  Tính đạo hàm hàm số có dạng U/V
G11.11  Tìm đạo hàm của hàm số cho trước
G11.12  Tìm đạo hàm của hàm số cho trước

G11+12.1   Tính đạo hàm ,tích phân , giới hạn , vẽ đồ thị


LƯỢNG GIÁC 11

L11.1   Giải phương trình lượng giác
L11.2   Giải phương trình lượng giác trên một đoạn
L11.3   Tìm chu kỳ của hàm số tuần hoàn
L11.4   Khai triển công thức lượng giác



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 12

D12.1   Cấu trúc của số phức
D12.1   Giải phương trình mũ
D12.3   Giải  phương trình chứa tham số
D12.4   Giải  phương trình  bất kỳ  ( Bậc 2 , 3 , ... , mũ  , log , căn thức )
D12.5   Giải phương trình mũ



GIẢI TÍCH 12


G12.1  Vẽ đồ thị biểu diễn phương trình
G12.2    Khảo sát hàm số hữu tỷ
G12.3   Vẽ đồ thị trong toạ độ cực (Polar)
G12.4    Tìm cực trị của hàm số
G12.5    Vẽ đồ thị hàm số 2D
G12.6   Tìm đạo hàm cấp 2 của hàm số
G12.7    Vẽ nhiều hàm số - Basic plot. To plot two or more functions, enter {f1(x), f2(x),...}
G12.8    Tìm điểm uốn của hàm số cho trước
G12.9    Tìm nghiệm của các phương trình  y = 0 , y ' = 0 ,  y " = 0
G12.10    Tính tích phân bất định
G12.11    Tính tích phân bất định minh hoạ từng bước
G12.12   Tính tích phân bất định minh hoạ từng bước
G12.13   Tìm đường tiệm cận của hàm số
G12.14   Tính diện tích hình phẳng giới hạn bởi 2 đường cong (C1) , (C2)
G12.15  Tìm giao điểm của hàm số đa thức và trục hoành Ox - Vẽ đồ thị .
G12.16    Tính thể tích vật thể tròn xoay giới hạn bởi (C1) , (C2)
G12.17    Vẽ đồ thị hàm số ( có đường tiệm cận )
G12.18   Vẽ đồ thị 2D , 3D
G12.19   Tìm hoành độ giao điểm giữa 2 đường cong (C1) , (C2)
G12.20    Vẽ đường cong tham số 3D
G12.21    Tính diện tich mặt tròn xoay
G12.22    Tích thể tích vật tròn xoay  (C) , trục  Ox , x =a , x= b
G12.23    Thể tích vật tròn xoay
G12.24    Tích thể tích vật tròn xoay (C1) , (C2) , trục OX , x = a , x = b
G12.25    Khảo sát hàm số đơn giản
G12.26    Tìm cực trị của hàm số
G12.27    Tìm nguyên hàm của hàm số
G12.28    Tính tích phân xác định


HÌNH HỌC 12

H12.1  Tính khoảng cách 2 điểm trong 2D , 3D
H12.2   Viết phương trình mặt phẳng qua 3 điểm trong không gian
H12.3  Viết phương trình tham số của đường thẳng trong không gian
H12.4   Tìm công thức thể tích , diện tích hình không gian
H12.5   Vẽ đồ thị 2D , mặt 3D
H12.6    Tích có hướng 2 vector



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

GIẢI TÍCH CAO CẤP

GI.1    Vẽ đồ thị , mặt 3D
GI.2   Vẽ đồ thị , mặt  3D
GI.3    Tích phân 2 lớp
GI.5    Tích phân kép
GI.6    Tích phân bội 3
GI.7    Tích phân bội 3
GI.8    Tích phân suy rộng
GI.9    Chuỗi và dãy số
GI.10    Các bài toán cơ bản trong vi  tích phân
GI.11     Vẽ hàm từng khúc ( piecewise ) - dùng để xét tính liên tục của hàm số
GI.12    Tính đạo hàm và tích phân một hàm số cho trước
GI.13     Vẽ đồ thị hàm số trong hệ toạ độ cực
GI.14     Tính đạo hàm riêng
GI.15    Khai triển hàm số bằng đa thức TAYLOR
GI.16    Tính tổng chuỗi số  n = 1...$\infty$
GI.17     Vẽ  đồ thị  3 hàm số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Bài viết sau đây mô tả các khái niệm toán học và hướng dẫn tính toán chi tiết bằng công cụ trực tuyến , bạn đọc có thể tham khảo những nội dung chính yếu được đề cập đến trong giáo trình toán phổ thông  cùng với các ví dụ minh họa  .

Một số website hữu ích phục vụ cho việc giảng dạy và học tập môn toán :

http://quickmath.com/
http://analyzemath.com/
http://www.intmath.com/
http://www.mathportal.org
https://www.mathway.com/
https://www.symbolab.com/
http://www.graphsketch.com/
http://www.meta-calculator.com/online/?home
http://cohtrantmed.yolasite.com/widgets-tructuyen

13.  XỬ LÝ DỮ LIỆU  - phân phối chuẩn  .

13.5  Áp dụng phân phối chuẩn .

13.5.1  Các ví dụ về khoảng tin cậy .

a. Cách tìm khoảng tin cậy .

+Bước 1.  Gọi số phần tử của mẫu là  n, tìm giá trị trung bình   $\bar{X}$  và độ lệch chuẩn $\sigma$  of của mẫu :


Bước 2.  Chọn khoảng tin cậy CI - Confidence Interval theo yêu cầu , thông thường là  90%, 95% hay 99% . Tìm giá trị  Z  tương ứng với CI  theo bảng sau :

           Z
80%        1,282
85%        1,440
90%        1,645
95%        1,960
99%        2,576
99,5%     2,807
99,9%     3,291


Bước 3: Dùng giá trị Z tìm được cho công thức khoảng tin cậy CI như sau


 $\overline{X}\pm Z\frac{\sigma }{\sqrt{n}}$

Trong đó

     $\overline{X}$ là giá trị trung bình
    Z  là giá trị được chọn tương ứng với tỷ lệ tin cậy
    $\sigma$ là độ lệch chuẩn
    n  là số phần tử của mẫu


*Truy cập    https://www.mathsisfun.com/data/confidence-interval-calculator.html

b. Các ví dụ .

Ví dụ 1. 
Khảo sát trọng lượng của 30 trái thanh long được chọn ngẫu nhiên, ta có :
     +Trọng lượng trung bình  86 g,
     +Độ lệch chuẩn 20g.
Hãy tìm độ tin cậy ứng với tỷ lệ 95%


Giá trị trung bình $\overline{X}$ = 86
Độ lệch chuẩn  $\sigma$ = 20
Số phần tử của mẫu    n = 30

Công thức

 $\overline{X}\pm Z\frac{\sigma }{\sqrt{n}}$ =  $86 \pm 1.960\frac{5}{\sqrt{30}}$ = $86 \pm 1.79$

Ví dụ 2. 
Một mẫu gồm 30 quả cam được lựa chọn ngẫu nhiên  lấy từ một tổng thể, sau khi đo thì có đường kính trung bình của mẫu là 91 mm và độ lệch chuẩn là 8 mm.

Tính (chính xác đến một số thập phân) giới hạn đường kính trung bình của toàn bộ tổng thể với độ tin cậy 85% .



Truy cập  https://www.mathsisfun.com/data/confidence-interval-calculator.html

85% Confidence Interval: 91 ± 2.1
(88.9 to 93.1)

Short Style: 91 (85% CI 88.9 to 93.1)

Margin of Error: 2.1
(With more digits: 2.103)

Sample Size: 30
Sample Mean: 91
Sample Standard Deviation: 8
Confidence Level: 85%

Ví dụ 3.
Thời gian của 8 vận động viên chạy nước rút  100 m tại Thế vận hội Olympic trung bình là 9.84 s và độ lệch chuẩn 0.08 s.

Tính thời gian trung bình (chính xác đến hai chữ số thập phân) với độ tin cậy 99.9%  .



99.9% Confidence Interval: 9.84 ± 0.093
(9.747 to 9.933)

Short Style: 9.84 (99.9% CI 9.747 to 9.933)

Margin of Error: 0.093
(With more digits: 0.09307)

Sample Size: 8
Sample Mean: 9.84
Sample Standard Deviation: 0.08
Confidence Level: 99.9%

Ví dụ 4.
Một cuốn sách có 500 trang không tính bìa .
Lấy mẫu ngẫu nhiên gồm 25 trang của cuốn sách này , đếm số từ trên mỗi trang . Số lượng trung bình của từ của mẫu là 323 từ và độ lệch chuẩn là 38.4 từ.

Tính số lượng trung bình các từ (chính xác đến số nguyên gần nhất) với độ tin cậy 80% . Tính số lượng trung bình các từ  cho toàn cuốn sách .


80% Confidence Interval: 323 ± 9.8
(313.2 to 332.8)

Short Style: 323 (80% CI 313.2 to 332.8)

Margin of Error: 9.8
(With more digits: 9.842)

Sample Size: 25
Sample Mean: 323
Sample Standard Deviation: 38.4
Confidence Level: 80%

Sau khi làm tròn số lượng trung bình các từ (chính xác đến số nguyên gần nhất) với độ tin cậy 80%  là giữa 313 và 333 .
Trung bình tốt nhất là  (313 + 333)/2 = 323 từ
Tính số lượng trung bình các từ cho toàn cuốn sách  323 x 500 = 161500 (từ)


Ví dụ 5.
Điều tra về điểm thi giữa kỳ môn Khoa học của một mẫu , ta có bảng sau
Hãy tính
a. Điểm trung bình mẫu
b. Độ lệch chuẩn mẫu
c. Khoảng tin cậy của điểm trung bình mẫu với độ tin cậy 85%

Điểm số  x	0	1	2	3	4	5	6	7	8	9	10
Tần số f	1	0	1	4	7	8	4	1	0	3	1

*Truy cập  http://www.meta-calculator.com/online/?panel-401-basic-stats-input
Nhập liệu theo grouped data , Click Calculate Statistics tìm được n = 30 , trung bình = 5 , độ lệch chuẩn = 2.181

*Truy cập  https://www.mathsisfun.com/data/confidence-interval-calculator.html

85% Confidence Interval: 5 ± 0.57
(4.43 to 5.57)

Short Style: 5 (85% CI 4.43 to 5.57)

Margin of Error: 0.57
(With more digits: 0.5732)

Sample Size: 30
Sample Mean: 5
Sample Standard Deviation: 2.181
Confidence Level: 85%

13.5.2  Các tính chất đặc trưng của phân phối chuẩn .

a. Quan giữa độ lệch chuẩn và phân phối chuẩn .

1.Biểu đồ sau minh họa tính chất của phân phối chuẩn


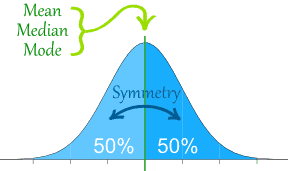
Các giá trị trung bình , trung vị , thường số gần như bằng nhau .
Đồ thị phân phối chuẩn có hình chuông và trục đối xứng .
50% giá trị nhỏ hơn trung bình , 50% giá trị lớn hơn trung bình .

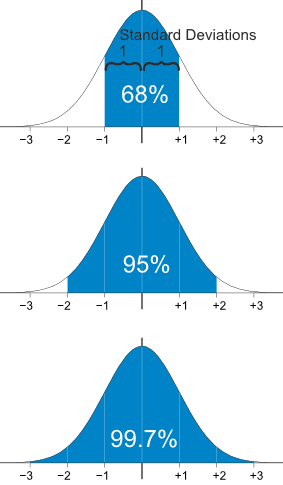
2. Liên hệ giữa độ lệch chuẩn và tỷ lệ giá trị thuộc phân phối chuẩn 

Sự liên hệ được biểu diễn như hình sau
Độ lệch 1 sigma  : chứa 68%
Độ lệch 2 sigma  : chứa 95%
Độ lệch 1 sigma  : chứa 99.7%

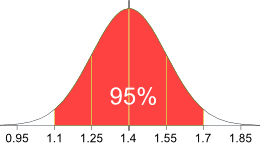
Ví dụ 6.   Điều tra về chiều cao của học sinh tại Maryland Highschool cho thấy  95% học sinh ở trường có chiều cao từ 1.1m đến 1.7m . Giả sử dữ liệu này có phân phối chuẩn , hãy tìm giá trị trung bình và độ lệch chuẩn?



Giá trị trung bình nằm giữa 1.1m và 1.7m:
Có nghĩa là  $\mu$= (1.1m + 1.7m) / 2 = 1.4m
Với tỷ lệ 95% tương ứng là 2 độ lệch chuẩn ở hai bên của trung bình $\mu$ (tổng cộng 4 lần độ lệch chuẩn) như vậy:
1 độ lệch chuẩn = (1.7m-1.1m) / 4 = 0.6m / 4 = 0.15m
Do đó  $\sigma$ = 0.15m

Xem hình sau


Khi biết độ lệch chuẩn $\sigma$, chúng ta có thể xác định bất kỳ một giá trị nào của phân phối là:
-có khả năng nằm trong khoảng 1 độ lệch chuẩn (68%)
-rất có thể nằm trong khoảng 2 độ lệch chuẩn (95%)
-gần như chắc chắn trong khoảng 3 độ lệch chuẩn (99.7% )

b. Số tiêu chuẩn  z-score .
1. Số lượng các độ lệch chuẩn - z-score .
Số lượng các độ lệch chuẩn tính từ giá trị trung bình cũng được gọi là "số tiêu chuẩn ", "sigma" hoặc "z-score".

Ví dụ 7.   Trong cùng trường  Maryland Highschool bạn Andre có chiều cao là 1.85m .
Bạn có thể nhìn thấy trên đường cong hình chuông trị số 1.85m là cách 3 độ lệch chuẩn tính từ trung bình 1.4, vì vậy chiều cao của Andre có một "z-score" bằng 3

Ta cũng có thể tính toán số lượng các độ lệch chuẩn của 1,85 tính từ giá trị trung bình là bao nhiêu như sau :

+Trước hết tính độ xa của 1.85 với giá trị trung bình

Độ xa = 1.85 - 1.4 = 0.45m (tính từ trung bình là 1.4)
++Kế tiếp tính số lượng độ lệch chuẩn - z-score :
Với độ lệch chuẩn là 0,15m ta có :
0,45m / 0,15m = 3 độ lệch chuẩn
vậy Z-score = 3  (xem hình)


2. Chuyển một trị số trong phân phối về z-score .
Muốn chuyển đổi một trị số về một số tiêu chuẩn ("z-score") ta cần thực hiện 2 bước :

    Bước 1. lấy trị số đó trừ đi giá trị trung bình $x- \mu$,
    Bước 2. lấy kết quả chia cho độ lệch chuẩn $(x- \mu) / \sigma$

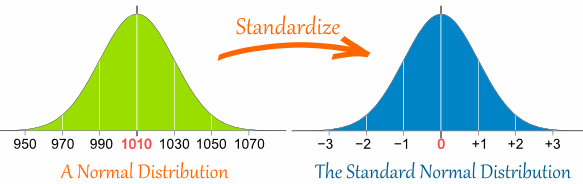
Thực hiện điều đó được gọi là "Chuẩn hóa" (Standardize) :

Với cách thức này chúng ta có thể lấy bất kỳ một phân phối thường nào (Normal Distribution) và chuyển đổi nó thành phân phối chuẩn (Standard Normal Distribution).



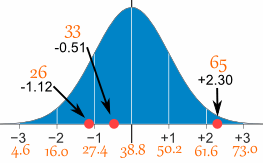
Ví dụ 8.  Một cuộc khảo sát về thời gian đến trường hàng ngày của Mike có những kết quả (đơn vị : phút) như dưới đây :

26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34
Tìm giá trị trung bình , độ lệch chuẩn và chuyển đổi trị số 26 về  z-score
*Truy cập   https://www.mathsisfun.com/data/standard-deviation-calculator.html

Giá trị trung bình là 38.8 phút, và độ lệch chuẩn là 11.7 phút  .
Hãy chuyển đổi trị số 26 về z-score ("số tiêu chuẩn").

Để chuyển đổi trị số 26 về -score ta tính :
Bước 1. lấy trị số trừ đi giá trị trung bình: $x- \mu$ = 26 - 38.8 = -12.8
Bước 2. lấy kết quả chia cho độ lệch chuẩn: $(x- \mu) / \sigma$  = -12.8 / 11.7 = -1,0940

Vì vậy, trị số 26 có z-score = -1,0940 độ lệch chuẩn tính từ giá trị trung bình 38.8

Tương tự dưới đây là chuyển đổi của 3 trị số đầu tiên
Trị số ban đầu          Bước tính               (Z-score)
26                            (26-38,8) / 11,7 = -1,0940
33                            (33-38,8) / 11,7 = -0,4957
65                            (65-38,8) / 11,7 = +2,2393
... ... ...
Tiếp tục cho các trị số còn lại trong phân phối
Biểu đồ minh họa


3. Công thức tính z-score .
Dưới đây là công thức cho z-score mà chúng ta đã sử dụng:



     z là "z-score" (số tiêu chuẩn)
     x là trị số trong phân phối cần được chuẩn hóa
     μ là giá trị trung bình của phân phối
     σ là độ lệch chuẩn


Việc chuẩn hóa có thể giúp chúng ta đưa ra những ước lượng và quyết định tốt hơn về dữ liệu có trong phân phối .
Ví dụ 9. Khảo sát thực nghiệm trên điểm thi  học kỳ  6 môn của 11 học sinh Maryland Highschool .

Dưới đây là những kết quả ( đơn vị : trên 60 điểm)

20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17

Hầu hết các học sinh này đều không vượt qua kỳ thi thậm chí có những học sinh  không đạt được 30 / 60 . Việc kiểm tra đã thực sự gặp khó khăn.  Do đó, các giáo sư quyết định Chuẩn hóa tất cả các điểm số và chỉ đánh rớt học sinh nào có tổng điểm trung bình dưới 1 độ lệch chuẩn. Hãy xác định xem học sinh nào sẽ bị đánh trượt .


*Truy cập   https://www.mathsisfun.com/data/standard-deviation-calculator.html
 Count:
11(How many numbers)
Sum:
253(All the numbers added up)
Mean:
23
Standard Deviation:
6.633249581
 -----------------------------------
Giá trị trung bình là 23 và độ lệch chuẩn là 6,6, và đây là những số tiêu chuẩn z-score tương ứng của 11 học sinh :

Trị số ban đầu          Bước tính            (Z-score)

20                            (20-23) / 6.6 =   -0,4545
15                            (15-23) / 6.6 =   -1,2121  (*)
26                            (26-23) / 6.6 =    0,4545
32                            (32-23) / 6.6 =    1,3636
18                            (18-23) / 6.6 =   -0,7576
28                            (28-23) / 6.6 =    0,7576
35                            (35-23) / 6.6 =    1,8182
14                            (14-23) / 6.6 =   -1,3636  (*)
26                            (26-23) / 6.6 =    0,4545
22                            (22-23) / 6.6 =   -0,1515
17                            (17-23) / 6.6 =   -0,9091

Dựa vào các z-score  , chỉ có 2 học sinh viên sẽ bị đánh trượt , đó là những học sinh đã có điểm thi 15 và 14 vì các z-score (-1,2121 và -1,3636 )  đều dưới 1 độ lệch chuẩn .


c. Tìm tỷ lệ %  và tỷ lệ tích lũy tiêu chuẩn dựa vào  z-score .
1. Biểu đồ phân phối chuẩn - tỷ lệ phần trăm .
Biểu đồ sau đây mô tả phân phối chuẩn với tỷ lệ phần trăm cho mỗi nửa của một độ lệch chuẩn, và tỷ lệ tích lũy tiêu chuẩn 


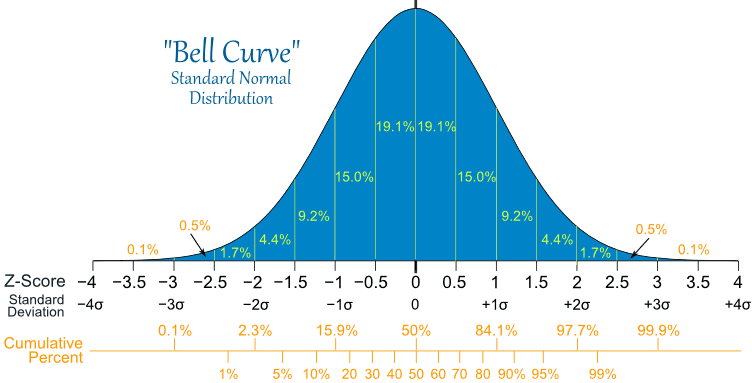
Ví dụ 10.   Điểm số môn Toán của Mike trong một thử nghiệm gần đây là 0.5 độ lệch chuẩn trên mức trung bình, Hỏi tỷ lệ % số bạn trong cùng lớp đã có điểm thấp hơn Mike ?

Dựa vào biểu đồ trên ta dễ dàng nhận thấy





     Tỷ lệ giữa 0 và 0.5 là 19.1%
     Tỷ lệ nhỏ hơn 0 là 50% (nửa bên trái của đường cong)

Như vậy tỷ lệ tổng cộng ít hơn bạn Mike là:

50% + 19.1% = 69.1%

Trên lý thuyết có 69.1% là  tỷ lệ số bạn có điểm ít hơn bạn Mike  (nhưng với dữ liệu thực tế tỷ lệ này có thể khác đi)


2. Bảng phân phối chuẩn
Chúng ta cũng có thể dùng phương pháp tra bảng z-score để tìm tỷ lệ % của tổng thể (hoặc mẫu) tương ứng .

Z	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,0000	0,0040	0,0080	0,0120	0,0160	0,0199	0,0239	0,0279	0,0319	0,0359
0,1	0,0398	0,0438	0,0478	0,0517	0,0557	0,0596	0,0636	0,0675	0,0714	0,0753
0,2	0,0793	0,0832	0,0871	0,0910	0,0948	0,0987	0,1026	0,1064	0,1103	0,1141
0,3	0,1179	0,1217	0,1255	0,1293	0,1331	0,1368	0,1406	0,1443	0,1480	0,1517
0,4	0,1554	0,1591	0,1628	0,1664	0,1700	0,1736	0,1772	0,1808	0,1844	0,1879
0,5	0,1915	0,1950	0,1985	0,2019	0,2054	0,2088	0,2123	0,2157	0,2190	0,2224
0,6	0,2257	0,2291	0,2324	0,2357	0,2389	0,2422	0,2454	0,2486	0,2517	0,2549
0,7	0,2580	0,2611	0,2642	0,2673	0,2704	0,2734	0,2764	0,2794	0,2823	0,2852
0,8	0,2881	0,2910	0,2939	0,2967	0,2995	0,3023	0,3051	0,3078	0,3106	0,3133
0,9	0,3159	0,3186	0,3212	0,3238	0,3264	0,3289	0,3315	0,3340	0,3365	0,3389
1,0	0,3413	0,3438	0,3461	0,3485	0,3508	0,3531	0,3554	0,3577	0,3599	0,3621
1,1	0,3643	0,3665	0,3686	0,3708	0,3729	0,3749	0,3770	0,3790	0,3810	0,3830
1,2	0,3849	0,3869	0,3888	0,3907	0,3925	0,3944	0,3962	0,3980	0,3997	0,4015
1,3	0,4032	0,4049	0,4066	0,4082	0,4099	0,4115	0,4131	0,4147	0,4162	0,4177
1,4	0,4192	0,4207	0,4222	0,4236	0,4251	0,4265	0,4279	0,4292	0,4306	0,4319
1,5	0,4332	0,4345	0,4357	0,4370	0,4382	0,4394	0,4406	0,4418	0,4429	0,4441
1,6	0,4452	0,4463	0,4474	0,4484	0,4495	0,4505	0,4515	0,4525	0,4535	0,4545
1,7	0,4554	0,4564	0,4573	0,4582	0,4591	0,4599	0,4608	0,4616	0,4625	0,4633
1,8	0,4641	0,4649	0,4656	0,4664	0,4671	0,4678	0,4686	0,4693	0,4699	0,4706
1,9	0,4713	0,4719	0,4726	0,4732	0,4738	0,4744	0,4750	0,4756	0,4761	0,4767
2,0	0,4772	0,4778	0,4783	0,4788	0,4793	0,4798	0,4803	0,4808	0,4812	0,4817
2,1	0,4821	0,4826	0,4830	0,4834	0,4838	0,4842	0,4846	0,4850	0,4854	0,4857
2,2	0,4861	0,4864	0,4868	0,4871	0,4875	0,4878	0,4881	0,4884	0,4887	0,4890
2,3	0,4893	0,4896	0,4898	0,4901	0,4904	0,4906	0,4909	0,4911	0,4913	0,4916
2,4	0,4918	0,4920	0,4922	0,4925	0,4927	0,4929	0,4931	0,4932	0,4934	0,4936
2,5	0,4938	0,4940	0,4941	0,4943	0,4945	0,4946	0,4948	0,4949	0,4951	0,4952
2,6	0,4953	0,4955	0,4956	0,4957	0,4959	0,4960	0,4961	0,4962	0,4963	0,4964
2,7	0,4965	0,4966	0,4967	0,4968	0,4969	0,4970	0,4971	0,4972	0,4973	0,4974
2,8	0,4974	0,4975	0,4976	0,4977	0,4977	0,4978	0,4979	0,4979	0,4980	0,4981
2,9	0,4981	0,4982	0,4982	0,4983	0,4984	0,4984	0,4985	0,4985	0,4986	0,4986
3,0	0,4987	0,4987	0,4987	0,4988	0,4988	0,4989	0,4989	0,4989	0,4990	0,4990

Trần hồng Cơ
Ngày 20/03/2016



------------------------------------------------------------------------------------------- 

 If you know about what you are talking about , you have something more valuable than gold and jewels - 

Có nhiều vàng và châu ngọc , nhưng miệng có tri thức là bửu vật quý giá vô song . 

Châm ngôn 20:15