GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN . Phần 13d . XỬ LÝ DỮ LIỆU - Khoảng tin cậy .

GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN .

Phần 13d . XỬ LÝ DỮ LIỆU  - Khoảng tin cậy .   

DANH MỤC CÔNG CỤ GIẢI TOÁN TRỰC TUYẾN  MATHEMATICA  WOLFRAM | ALPHA .

Giới thiệu .

Bạn đọc truy cập vào đường dẫn  http://cohtrantmed.yolasite.com/widgets-tructuyen  để sử dụng các widgets giải toán trực tuyến W|A Mathematica theo chỉ mục trong danh sách dưới đây .

Những widgets này đã được tác giả sắp xếp theo từng môn học và cấp lớp theo ký hiệu như sau :

D : Đại số . Ví dụ  D8.1 widget dùng cho Đại số lớp 8 , mục 1 - Khai triển , rút gọn biểu thức đại số .
H : Hình học . Ví dụ  H12.3  widget dùng cho Hình học lớp 12 , mục 3 - Viết phương trình tham số của đường thẳng trong không gian .
G : Giải tích . Ví dụ : G11.7  widget dùng cho Giải tích lớp 11 , mục 7 - Tính đạo hàm cấp cao của hàm số
GI : Giải tích cao cấp I . Ví dụ GI.15  widget dùng cho Giải tích cao cấp I , mục 15 - Khai triển hàm số bằng đa thức TAYLOR
GII : Giải tích cao cấp II .


++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


 ĐẠI SỐ 8

D8.1  Khai triển , rút gọn biểu thức đại số
D8.2  Rút gọn phân thức
D8.3  Phân tích thừa số
D8.4  Nhân 2 đa thức
D8.5  Khai triển tích số ( có thể dùng để khai triển Newton )
D8.6  Phân tích thừa số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 10

D10.1 Giải phương trình nguyên Diophante
D10.2 Giải phương trình tuyệt đối
D10.3 Giải phương trình chứa tham số
D10.4  Giải phương trình đại số
D10.5  Giải phương trình từng bước
D10.6  Giải bất phương trình minh hoạ bằng đồ thị

D10.8  Tính giá trị biểu thức hàm số
D10.9  Giải bất phương trình đại số và minh hoạ bằng đồ thị
D10.10  Giải bất phương trình đại số - tìm miền nghiệm
D10.11  Giải phương trình đại số
D10.12  Giải phương trình vô tỷ
D10.13  Giải phương trình minh hoạ từng bước
D10.14  Giải phương trình dạng hàm ẩn
D10.15  Giải hệ thống phương trình tuyến tính , phi tuyến
D10.16  Giải hệ phương trình
D10.17  Vẽ miền nghiệm của bất phương trình đại số
D10.19  Tối ưu hoá hàm 2 biến với các ràng buộc
D10.20  Tìm giao điểm của đồ thị hàm số và trục hoành Ox , trục tung Oy

HÌNH HỌC 10

H10.1  Tính diện tích tam giác trong hệ toạ độ Oxy
H10.3  Khảo sát conic ( đường tròn , Ellipse , Parabola , Hyperbola )
H10.2  Tính khoảng cách từ 1 điểm đến đường thẳng trong Oxy



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 11

D11.1 Thuật chia Euclide dùng cho số và đa thức  ( HORNER )
D11.2  Tính tổng nghịch đảo của n số tự nhiên




D11.6  Khai triển nhị thức Newton


GIẢI TÍCH 11


G11.1  Tính gíá trị một chuỗi số  theo n
G11.2  Đa thức truy hồi
G11.3  Khảo sát tính hội tụ của chuỗi số
G11.4  Tính giới hạn của chuỗi số khi  $n \rightarrow  \infty$
G11.5  Tìm hàm số ngược của hàm số cho trước
G11.6  Tìm đạo hàm của hàm số hợp - giải thích
G11.7   Tính đạo hàm cấp cao của hàm số
G11.8   Tìm giới hạn của hàm số
G11.9   Tìm giới hạn của hàm số
G11.10  Tính đạo hàm hàm số có dạng U/V
G11.11  Tìm đạo hàm của hàm số cho trước
G11.12  Tìm đạo hàm của hàm số cho trước

G11+12.1   Tính đạo hàm ,tích phân , giới hạn , vẽ đồ thị


LƯỢNG GIÁC 11

L11.1   Giải phương trình lượng giác
L11.2   Giải phương trình lượng giác trên một đoạn
L11.3   Tìm chu kỳ của hàm số tuần hoàn
L11.4   Khai triển công thức lượng giác



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 12

D12.1   Cấu trúc của số phức
D12.1   Giải phương trình mũ
D12.3   Giải  phương trình chứa tham số
D12.4   Giải  phương trình  bất kỳ  ( Bậc 2 , 3 , ... , mũ  , log , căn thức )
D12.5   Giải phương trình mũ



GIẢI TÍCH 12


G12.1  Vẽ đồ thị biểu diễn phương trình
G12.2    Khảo sát hàm số hữu tỷ
G12.3   Vẽ đồ thị trong toạ độ cực (Polar)
G12.4    Tìm cực trị của hàm số
G12.5    Vẽ đồ thị hàm số 2D
G12.6   Tìm đạo hàm cấp 2 của hàm số
G12.7    Vẽ nhiều hàm số - Basic plot. To plot two or more functions, enter {f1(x), f2(x),...}
G12.8    Tìm điểm uốn của hàm số cho trước
G12.9    Tìm nghiệm của các phương trình  y = 0 , y ' = 0 ,  y " = 0
G12.10    Tính tích phân bất định
G12.11    Tính tích phân bất định minh hoạ từng bước
G12.12   Tính tích phân bất định minh hoạ từng bước
G12.13   Tìm đường tiệm cận của hàm số
G12.14   Tính diện tích hình phẳng giới hạn bởi 2 đường cong (C1) , (C2)
G12.15  Tìm giao điểm của hàm số đa thức và trục hoành Ox - Vẽ đồ thị .
G12.16    Tính thể tích vật thể tròn xoay giới hạn bởi (C1) , (C2)
G12.17    Vẽ đồ thị hàm số ( có đường tiệm cận )
G12.18   Vẽ đồ thị 2D , 3D
G12.19   Tìm hoành độ giao điểm giữa 2 đường cong (C1) , (C2)
G12.20    Vẽ đường cong tham số 3D
G12.21    Tính diện tich mặt tròn xoay
G12.22    Tích thể tích vật tròn xoay  (C) , trục  Ox , x =a , x= b
G12.23    Thể tích vật tròn xoay
G12.24    Tích thể tích vật tròn xoay (C1) , (C2) , trục OX , x = a , x = b
G12.25    Khảo sát hàm số đơn giản
G12.26    Tìm cực trị của hàm số
G12.27    Tìm nguyên hàm của hàm số
G12.28    Tính tích phân xác định


HÌNH HỌC 12

H12.1  Tính khoảng cách 2 điểm trong 2D , 3D
H12.2   Viết phương trình mặt phẳng qua 3 điểm trong không gian
H12.3  Viết phương trình tham số của đường thẳng trong không gian
H12.4   Tìm công thức thể tích , diện tích hình không gian
H12.5   Vẽ đồ thị 2D , mặt 3D
H12.6    Tích có hướng 2 vector



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

GIẢI TÍCH CAO CẤP

GI.1    Vẽ đồ thị , mặt 3D
GI.2   Vẽ đồ thị , mặt  3D
GI.3    Tích phân 2 lớp
GI.5    Tích phân kép
GI.6    Tích phân bội 3
GI.7    Tích phân bội 3
GI.8    Tích phân suy rộng
GI.9    Chuỗi và dãy số
GI.10    Các bài toán cơ bản trong vi  tích phân
GI.11     Vẽ hàm từng khúc ( piecewise ) - dùng để xét tính liên tục của hàm số
GI.12    Tính đạo hàm và tích phân một hàm số cho trước
GI.13     Vẽ đồ thị hàm số trong hệ toạ độ cực
GI.14     Tính đạo hàm riêng
GI.15    Khai triển hàm số bằng đa thức TAYLOR
GI.16    Tính tổng chuỗi số  n = 1...$\infty$
GI.17     Vẽ  đồ thị  3 hàm số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Bài viết sau đây mô tả các khái niệm toán học và hướng dẫn tính toán chi tiết bằng công cụ trực tuyến , bạn đọc có thể tham khảo những nội dung chính yếu được đề cập đến trong giáo trình toán phổ thông  cùng với các ví dụ minh họa  .

Một số website hữu ích phục vụ cho việc giảng dạy và học tập môn toán :

http://quickmath.com/
http://analyzemath.com/
http://www.intmath.com/
http://www.mathportal.org
https://www.mathway.com/
https://www.symbolab.com/
http://www.graphsketch.com/
http://www.meta-calculator.com/online/?home
http://cohtrantmed.yolasite.com/widgets-tructuyen

13.  XỬ LÝ DỮ LIỆU  - Khoảng tin cậy  .

13.4  Khoảng tin cậy - Độ tin cậy .

13.4.1  Khái niệm về khoảng tin cậy .

a.Định nghỉa

-Trong thống kê, khoảng tin cậy (confidence interval - CI)  là  khoảng ước lượng của một loại tham số nào đó xét về mặt tổng thể . Đó là một khoảng quan sát (nghĩa là nó được tính toán từ các quan sát), về nguyên tắc có các khoảng tin cậy khác nhau theo các mẫu khác nhau , thường bao gồm giá trị của một tham số nào đó không quan sát được và tham số này cần được quan tâm đến nếu thực nghiệm được lặp đi lặp lại. Khoảng quan sát thường xuyên có chứa tham số được xác định bởi mức độ tin cậy hay hệ số tín nhiệm.
-Cụ thể hơn, ý nghĩa của thuật ngữ "độ tin cậy" là, nếu khoảng tin cậy CI được xây dựng qua nhiều sự phân tích dữ liệu thực nghiệm riêng biệt mở rộng (và có thể khác nhau), tỷ lệ khoảng đó có chứa các giá trị thực của tham số sẽ phù hợp với mức độ tin cậy cho trước.
-Khoảng tin cậy CI bao gồm một loạt các giá trị (khoảng) có chức hoạt như các ước lượng khá tốt của các tham số tổng thể chưa biết; Tuy nhiên, khoảng được tính từ một mẫu cụ thể không nhất thiết phải bao gồm các giá trị thực của tham số.  Mức tin cậy  99%  các giá trị của tham số thể hiện rằng 99% của khoảng tin cậy giả thuyết sẽ giữ giá trị thực sự của các tham số quan sát .
-Trong thực tế ứng dụng, khoảng tin cậy thường được ghi nhận ở mức độ tin cậy 95%.  Tuy nhiên, khi trình bày bằng hình vẽ, khoảng tin cậy có thể được thể hiện ở nhiều cấp độ khác nhau , ví dụ 90%, 95% và 99%. Một số yếu tố có thể ảnh hưởng đến kích thước khoảng tin cậy bao gồm kích thước của mẫu, độ tin cậy , và sự biến đổi tổng thể. Một kích thước mẫu lớn hơn thường sẽ dẫn đến một ước tính các tham số tốt hơn.

Ví dụ 1. 
Khảo sát chiều cao của 40 sinh viên được chọn ngẫu nhiên, và có được :
     +Chiều cao trung bình  175cm,
     +Độ lệch chuẩn 20cm.

Khoảng tin cậy 95% được tính là:   175cm ± 6,2cm  hay  [168.8 , 181.2]

Điều này cho biết chiều cao trung bình thực của tất cả sinh viên có thể sẽ là giữa 168,8cm và 181,2cm. Nhưng nó có thể không phải như vậy !

Bạn nhận thấy " tỷ lệ 95%"  muốn nói lên rằng 95%  các quan sát thực nghiệm sẽ có trung bình chiều cao đúng như giá trị trong khoảng tin cậy , nhưng 5% còn lại sẽ không đúng .

b. Cách tìm khoảng tin cậy .

+Bước 1.  Gọi số phần tử của mẫu là  n, tìm giá trị trung bình   $\bar{X}$  và độ lệch chuẩn $\sigma$  of của mẫu :
Ở ví dụ 1
    Số phần tử của mẫu : n = 40
    Giá trị trung bình : $\overline{X}$ = 175
    Độ lệch chuẩn $\sigma$  = 20

Bước 2.  Chọn khoảng tin cậy CI - Confidence Interval theo yêu cầu , thông thường là  90%, 95% hay 99% . Tìm giá trị  Z  tương ứng với CI  theo bảng sau :

           Z
80%        1,282
85%        1,440
90%        1,645
95%        1,960
99%        2,576
99,5%     2,807
99,9%     3,291

Với ước lượng 95% thì giá trị của Z là  1,960

Bước 3: Dùng giá trị Z tìm được cho công thức khoảng tin cậy CI như sau


 $\overline{X}\pm Z\frac{\sigma }{\sqrt{n}}$

Trong đó

     $\overline{X}$ là giá trị trung bình
    Z  là giá trị được chọn tương ứng với tỷ lệ tin cậy
    $\sigma$ là độ lệch chuẩn
    n  là số phần tử của mẫu

Với số liệu ở ví dụ 1 , ta thu được
175 ± (1,960 × 20)/√40 = 175cm ± 6,20cm

Khoảng tin cậy : từ 168,8cm đến 181,2cm

*Truy cập    https://www.mathsisfun.com/data/confidence-interval-calculator.html

Ví dụ 2.  Chọn ngẫu nhiên một mẫu gồm 20 trái dưa hấu được được lấy từ một tổng thể lớn .Trọng lượng trung bình của mẫu là 105 lb (47.627 kg) và độ lệch chuẩn là 15 lb (6.803 kg) .

Tính (chính xác đến một số thập phân) giới hạn với 99,5% độ tin cậy cho trọng lượng trung bình của toàn bộ tổng thể dưa hấu.



Với độ tin cậy 99.5% , Z = 2.807
$\overline{X}$ = 105 , $\sigma $ = 15 , n = 20
Thế vào công thức  $\overline{X}\pm Z\frac{\sigma }{\sqrt{n}}$
Vậy các giới hạn với độ tin cậy 99.5% là  105 ± 9.4
Trọng lượng trung bình của toàn bộ tổng thể dưa hấu trong khoảng 95.6 lb. và 114.4 lb.

Xem hình

c. Phân phối chuẩn
Các giá trị Z theo " tỷ lệ Z " được tính toán dựa trên ý tưởng của phân phối chuẩn,
Ví dụ tỷ lệ Z 95% có giá trị là 1.960, và ở đây chúng ta thấy khoảng từ -1,96 đến +1,96 bao gồm 95% các giá trị quan sát thực nghiệm :

Từ -1,96 đến +1,96 độ lệch chuẩn là 95%

13.4.2  Phân phối thường  - NORMAL DISTRIBUTION
a. Khái niệm .
Dữ liệu thực nghiệm có thể được phân phối theo những cách khác nhau.
Nó có thể nằm rải rác về bên trái hoặc thiên về bên phải ,hoặc có thể được phân bố một cách tùy ý .

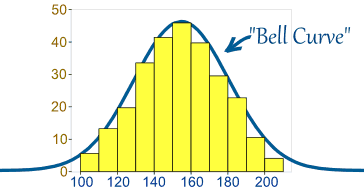
Nhưng có nhiều trường hợp các dữ liệu có xu hướng tập trung quanh một giá trị trung tâm ít lệch sang bên trái hoặc bên phải, và tiến gần đến một phân phối bình thường như sau

Phân phối có biểu đồ gần đối xứng , dạng chuông , với đa số điểm dữ liệu ở trung tâm , được gọi là phân phối thường .

Ví dụ 3. xem biểu đồ phân phối sau , lưu ý đến 3 chỉ số độ đo trung tâm rất gần nhau .

Khi đó các độ đo trung tâm -Measures of Centrality- khá gần nhau

  Trung bình -Mean: 16.0020

  Trung vị -Median: 16.0034

  Thường số -Mode: 16.0100

b. Tính chất .

Phân phối thường có 2 tính chất chính .

1.   Tần số của các điểm dữ liệu gần trung tâm ( hoặc trung bình ) là cao hơn tần số của các điểm dữ liệu xa trung tâm .

2.   Phân phối có tính đối xứng .

Vì những tính chất này nên trung bình , trung vị và thường số hầu như gần ở trung tâm phân phối .

Ví dụ 4.  Chiều cao của nhóm người được điều tra giả sử có thể mô tả bởi phân phối thường . Trung bình chiều cao là 66.5 inches , độ lệch chuẩn là 2.4 inches . Tìm và giải thích các khoảng biểu diễn cách đều 1 , 2 và 3 độ lệch chuẩn từ giá trị trung bình . ( xem hình )

c. Xác suất và diện tích .

Để tìm xác suất một biến ngẫu nhiên x  trong khoảng từ a đến b  , ta cần phải xác định diện tích của hình phẳng giới hạn từ a đến b .

d. Phân phối chuẩn -The Standard Normal Distribution
 Phân phối chuẩn là phân phối thường có trung bình bằng 0  và độ lệch chuẩn bằng 1 . Ta còn gọi phân phối chuẩn là phân phối Z .

Bạn có thể sử dụng phần mềm Distribution Calculator trực tuyến dưới đây , nhập giá trị trung bình , độ lệch chuẩn , X1 , X2 và click Calculate .  Đọc kết quả ở phần P(X1 to X2) 

NHẬP DỮ LIỆU Ở ĐÂY .
Distribution Calculator


**********************************************************************

b. p( z > 1.87 )  Dùng ESBPDF Analysis

Dùng phần mềm Distribution Calculator trực tuyến . Đọc kết quả ở phần P(X > X1)

Tương tự cho các ví dụ c. và d. 



13.4.3  Đổi sang phân phối Z - Converting to the Z-Distribution .
a. Quan hệ giữa phân phối thường và phân phối chuẩn  .

Ví dụ 6. Xét tổng thể được biểu diễn  bởi phân phối thường có $\mu= 24.6$  và 
độ lêch chuẩn $\sigma =  1.3$ . Hỏi có bao nhiêu phần trăm dữ liệu trong khoảng 25.3  và  26.8 ? 

Dùng phần mềm Distribution Calculator trực tuyến .
 Đọc kết quả ở phần P(X > X1) 

Dùng phần mềm Distribution Calculator trực tuyến .
  Đọc kết quả ở phần P(X > X1) 

Như vậy có xấp xỉ khoảng 24.9% dữ liệu trong khoảng 25.3 và 26.8 .

Ví dụ 7. Chiều cao của nhóm người Nhật được xem như có dạng phân phối thường . Trung bình chiều cao là  68 inches , độ lệch chuẩn là 4 inches . Tìm xác suất của các biến cố sau

a. cao hơn  73 inches
b.trong khoảng  60  và 75 inches .

b. Biên sai - Margin of Error  ( MOE )

Ví dụ 8 . Giả sử rằng với  độ tin cậy 90% trong chiến dịch bầu cử , hãy tìm biên sai trong các trường hợp sau

a. kích thước mẫu  n  =  275                
b.  kích thước mẫu  n  =  750

Cách  2  :  truy cập vào link sau   http://www.relevantinsights.com/research-tools
 Nhập liệu như hình sau , đọc MOE ( Margin of Error )


 

Điều này nghĩa là từ cuộc điều tra mẫu có 275 người , ta có độ tin cậy khoảng 90% mà sai số khả dĩ lớn nhất trong quy mô mẫu có thể cộng thêm hay bớt đi 5% điểm dữ liệu 

truy cập vào link    http://www.relevantinsights.com/research-tools
 Nhập liệu như hình sau , đọc MOE ( Margin of Error )












  























Ví dụ 9.  Trong cuộc điều tra 500 sinh viên đang học tại Đại học Yale , có 410 người trả lời rằng họ sẽ tốt nghiệp sau 4 năm .

a. Tìm quy mô mẫu thỏa mãn điều kiện  tốt nghiệp sau 4 năm .
b. Với độ tin cậy 95% , tìm biên sai MOE .
c. Giải thích các số liệu thu được .

Lời giải .

a. Quy mô mẫu là   410/500 = 0.82  = 82%
b. 

c. Tóm lại với độ tin cậy  95%  thì biên sai là  4.4%  , khi đó quy mô mẫu sẽ là   82%  + (-)  4.4%  . Đây là tỷ lệ sinh viên cho rằng sẽ tốt nghiệp sau 4 năm học .    

Nói cách khác là có khoảng từ 77.6%   đến  86.4%  tỷ lệ sinh viên Đại học Yale cho rằng sẽ tốt nghiệp sau 4 năm học .




Trần hồng Cơ
Ngày 15/03/2016




------------------------------------------------------------------------------------------- -

Những điều biết được chỉ là hạt cát , những điều chưa biết là cả một đại dương .

Isaac Newton