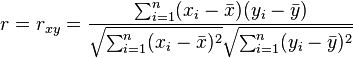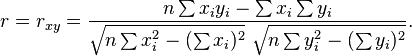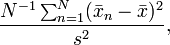Giải toán trực tuyến W | A




Vẽ đồ thị trong Oxyz plot3D(f(x,y),x=..,y=..)
Vẽ đồ thị trong Oxy plot(f(x),x=..,y=..)
Đạo hàm derivative(f(x))
Tích phân Integrate(f(x))


Giải toán trực tuyến W|A

Welcome to cohtran MMPC-VN Free Online Widgets and Solutions Galleries

MW

Thứ Ba, 23 tháng 2, 2016

GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN . Phần 13b . XỬ LÝ DỮ LIỆU - Hệ số tương quan .


 
GIẢI TOÁN PHỔ THÔNG BẰNG CÁC CÔNG CỤ TRỰC TUYẾN .

Phần 13b . XỬ LÝ DỮ LIỆU  -  Hệ số tương quan .   


DANH MỤC CÔNG CỤ GIẢI TOÁN TRỰC TUYẾN  MATHEMATICA  WOLFRAM | ALPHA .

Giới thiệu .

Bạn đọc truy cập vào đường dẫn  http://cohtrantmed.yolasite.com/widgets-tructuyen  để sử dụng các widgets giải toán trực tuyến W|A Mathematica theo chỉ mục trong danh sách dưới đây .

Những widgets này đã được tác giả sắp xếp theo từng môn học và cấp lớp theo ký hiệu như sau :

D : Đại số . Ví dụ  D8.1 widget dùng cho Đại số lớp 8 , mục 1 - Khai triển , rút gọn biểu thức đại số .
H : Hình học . Ví dụ  H12.3  widget dùng cho Hình học lớp 12 , mục 3 - Viết phương trình tham số của đường thẳng trong không gian .
G : Giải tích . Ví dụ : G11.7  widget dùng cho Giải tích lớp 11 , mục 7 - Tính đạo hàm cấp cao của hàm số
GI : Giải tích cao cấp I . Ví dụ GI.15  widget dùng cho Giải tích cao cấp I , mục 15 - Khai triển hàm số bằng đa thức TAYLOR
GII : Giải tích cao cấp II .


++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++


 ĐẠI SỐ 8

D8.1  Khai triển , rút gọn biểu thức đại số
D8.2  Rút gọn phân thức
D8.3  Phân tích thừa số
D8.4  Nhân 2 đa thức
D8.5  Khai triển tích số ( có thể dùng để khai triển Newton )
D8.6  Phân tích thừa số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 10

D10.1 Giải phương trình nguyên Diophante
D10.2 Giải phương trình tuyệt đối
D10.3 Giải phương trình chứa tham số
D10.4  Giải phương trình đại số
D10.5  Giải phương trình từng bước
D10.6  Giải bất phương trình minh hoạ bằng đồ thị

D10.8  Tính giá trị biểu thức hàm số
D10.9  Giải bất phương trình đại số và minh hoạ bằng đồ thị
D10.10  Giải bất phương trình đại số - tìm miền nghiệm
D10.11  Giải phương trình đại số
D10.12  Giải phương trình vô tỷ
D10.13  Giải phương trình minh hoạ từng bước
D10.14  Giải phương trình dạng hàm ẩn
D10.15  Giải hệ thống phương trình tuyến tính , phi tuyến
D10.16  Giải hệ phương trình
D10.17  Vẽ miền nghiệm của bất phương trình đại số
D10.19  Tối ưu hoá hàm 2 biến với các ràng buộc
D10.20  Tìm giao điểm của đồ thị hàm số và trục hoành Ox , trục tung Oy

HÌNH HỌC 10

H10.1  Tính diện tích tam giác trong hệ toạ độ Oxy
H10.3  Khảo sát conic ( đường tròn , Ellipse , Parabola , Hyperbola )
H10.2  Tính khoảng cách từ 1 điểm đến đường thẳng trong Oxy



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 11

D11.1 Thuật chia Euclide dùng cho số và đa thức  ( HORNER )
D11.2  Tính tổng nghịch đảo của n số tự nhiên




D11.6  Khai triển nhị thức Newton


GIẢI TÍCH 11


G11.1  Tính gíá trị một chuỗi số  theo n
G11.2  Đa thức truy hồi
G11.3  Khảo sát tính hội tụ của chuỗi số
G11.4  Tính giới hạn của chuỗi số khi  $n \rightarrow  \infty$
G11.5  Tìm hàm số ngược của hàm số cho trước
G11.6  Tìm đạo hàm của hàm số hợp - giải thích
G11.7   Tính đạo hàm cấp cao của hàm số
G11.8   Tìm giới hạn của hàm số
G11.9   Tìm giới hạn của hàm số
G11.10  Tính đạo hàm hàm số có dạng U/V
G11.11  Tìm đạo hàm của hàm số cho trước
G11.12  Tìm đạo hàm của hàm số cho trước

G11+12.1   Tính đạo hàm ,tích phân , giới hạn , vẽ đồ thị


LƯỢNG GIÁC 11

L11.1   Giải phương trình lượng giác
L11.2   Giải phương trình lượng giác trên một đoạn
L11.3   Tìm chu kỳ của hàm số tuần hoàn
L11.4   Khai triển công thức lượng giác



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

ĐẠI SỐ 12

D12.1   Cấu trúc của số phức
D12.1   Giải phương trình mũ
D12.3   Giải  phương trình chứa tham số
D12.4   Giải  phương trình  bất kỳ  ( Bậc 2 , 3 , ... , mũ  , log , căn thức )
D12.5   Giải phương trình mũ



GIẢI TÍCH 12


G12.1  Vẽ đồ thị biểu diễn phương trình
G12.2    Khảo sát hàm số hữu tỷ
G12.3   Vẽ đồ thị trong toạ độ cực (Polar)
G12.4    Tìm cực trị của hàm số
G12.5    Vẽ đồ thị hàm số 2D
G12.6   Tìm đạo hàm cấp 2 của hàm số
G12.7    Vẽ nhiều hàm số - Basic plot. To plot two or more functions, enter {f1(x), f2(x),...}
G12.8    Tìm điểm uốn của hàm số cho trước
G12.9    Tìm nghiệm của các phương trình  y = 0 , y ' = 0 ,  y " = 0
G12.10    Tính tích phân bất định
G12.11    Tính tích phân bất định minh hoạ từng bước
G12.12   Tính tích phân bất định minh hoạ từng bước
G12.13   Tìm đường tiệm cận của hàm số
G12.14   Tính diện tích hình phẳng giới hạn bởi 2 đường cong (C1) , (C2)
G12.15  Tìm giao điểm của hàm số đa thức và trục hoành Ox - Vẽ đồ thị .
G12.16    Tính thể tích vật thể tròn xoay giới hạn bởi (C1) , (C2)
G12.17    Vẽ đồ thị hàm số ( có đường tiệm cận )
G12.18   Vẽ đồ thị 2D , 3D
G12.19   Tìm hoành độ giao điểm giữa 2 đường cong (C1) , (C2)
G12.20    Vẽ đường cong tham số 3D
G12.21    Tính diện tich mặt tròn xoay
G12.22    Tích thể tích vật tròn xoay  (C) , trục  Ox , x =a , x= b
G12.23    Thể tích vật tròn xoay
G12.24    Tích thể tích vật tròn xoay (C1) , (C2) , trục OX , x = a , x = b
G12.25    Khảo sát hàm số đơn giản
G12.26    Tìm cực trị của hàm số
G12.27    Tìm nguyên hàm của hàm số
G12.28    Tính tích phân xác định


HÌNH HỌC 12

H12.1  Tính khoảng cách 2 điểm trong 2D , 3D
H12.2   Viết phương trình mặt phẳng qua 3 điểm trong không gian
H12.3  Viết phương trình tham số của đường thẳng trong không gian
H12.4   Tìm công thức thể tích , diện tích hình không gian
H12.5   Vẽ đồ thị 2D , mặt 3D
H12.6    Tích có hướng 2 vector



++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

GIẢI TÍCH CAO CẤP

GI.1    Vẽ đồ thị , mặt 3D
GI.2   Vẽ đồ thị , mặt  3D
GI.3    Tích phân 2 lớp
GI.5    Tích phân kép
GI.6    Tích phân bội 3
GI.7    Tích phân bội 3
GI.8    Tích phân suy rộng
GI.9    Chuỗi và dãy số
GI.10    Các bài toán cơ bản trong vi  tích phân
GI.11     Vẽ hàm từng khúc ( piecewise ) - dùng để xét tính liên tục của hàm số
GI.12    Tính đạo hàm và tích phân một hàm số cho trước
GI.13     Vẽ đồ thị hàm số trong hệ toạ độ cực
GI.14     Tính đạo hàm riêng
GI.15    Khai triển hàm số bằng đa thức TAYLOR
GI.16    Tính tổng chuỗi số  n = 1...$\infty$
GI.17     Vẽ  đồ thị  3 hàm số

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Bài viết sau đây mô tả các khái niệm toán học và hướng dẫn tính toán chi tiết bằng công cụ trực tuyến , bạn đọc có thể tham khảo những nội dung chính yếu được đề cập đến trong giáo trình toán phổ thông  cùng với các ví dụ minh họa  .

Một số website hữu ích phục vụ cho việc giảng dạy và học tập môn toán :

http://quickmath.com/
http://analyzemath.com/
http://www.intmath.com/
http://www.mathportal.org
https://www.mathway.com/
https://www.symbolab.com/
http://www.graphsketch.com/
http://www.meta-calculator.com/online/?home
http://cohtrantmed.yolasite.com/widgets-tructuyen



13.  XỬ LÝ DỮ LIỆU  - Hệ số tương quan .

13.2  Hệ số tương quan .

13.2.1  Khái niệm về hệ số tương quan .

a. Tương quan

Khi hai tập dữ liệu được liên kết chặt chẽ với nhau, ta nói rằng chúng có một sự tương quan cao. Sự tương quan có ý nghĩa là "quan hệ cùng nhau" .

     Tương quan là dương khi các giá trị cùng gia tăng với nhau (đồng biến)
     Tương quan là âm khi có một giá trị giảm trong khi một giá trị khác tăng (nghịch biến)

Ở đây chúng ta hãy thử nhìn vào mối tương quan tuyến tính (tương quan theo dạng đường thẳng) .


-Sự tương quan có thể biểu thị qua một giá trị gọi là hệ số tương quan .
Khi hệ số tương quan có giá trị :

     1 _ hai tập dữ liệu có một mối tương quan dương hoàn chỉnh .
     0 _ hai tập dữ liệu không có tương quan (các giá trị dường như không có mối liên quan với nhau ).
    -1 _ hai tập dữ liệu một mối tương quan âm hoàn chỉnh.

    Các giá trị này cho thấy cách thể hiện sự tương quan bằng độ dốc của đường thẳng là dương hay âm .

b.  Hệ số tương quan .
 
-Hệ số tương quan là hệ số minh họa độ đo định lượng của một số kiểu tương quan với nhau và phụ thuộc lẫn nhau - là các mối quan hệ thống kê giữa hai hoặc nhiều biến ngẫu nhiên hoặc các giá trị dữ liệu được quan sát.
-Các loại hệ số tương quan bao gồm:

+ Hệ số tương quan moment-tích Pearson , còn được gọi là r, R, hoặc r-Pearson, là một độ đo về cường độ và phương hướng của mối quan hệ tuyến tính giữa hai biến được định nghĩa là hiệp phương sai (mẫu) của các biến chia cho tích độ lệch chuẩn (mẫu) của chúng .

+Tương quan nội lớp (Intraclass), là một thống kê mô tả có thể được sử dụng khi các độ đo định lượng được thực hiện trên các đơn vị được tổ chức thành các nhóm; mô tả cách thức tương tác mạnh-yếu giữa các đơn vị trong cùng một nhóm giống nhau.

+Tương quan thứ bậc (Rank) , nghiên cứu về mối quan hệ giữa thứ bậc xếp hạng của các biến khác nhau hoặc xếp hạng khác nhau của cùng một biến .Trong tương quan thứ bậc còn có các hệ số khác nhau như :
*Hệ số tương quan bậc Spearman, một độ đo về mối quan hệ giữa hai biến có thể được mô tả bởi một hàm số đơn điệu.
*Hệ số tương quan bậc Kendall tau , một độ đo của phần ngạch cấp bậc phù hợp giữa hai tập dữ liệu.
*Hệ số tương quan bậc gamma Goodman-Kruskal, một độ đo về cường độ liên hợp của dữ liệu bảng khi cả hai biến được đo ở cấp thứ tự.

Mức hoàn hảo của sự phù hợp , cần lưu ý rằng mọi độ đo bất kỳ cho biết mức phù hợp như thế nào của một mô hình thống kê với quan sát bằng cách tổng kết sự chênh lệch giữa giá trị quan sát và các giá trị kỳ vọng ​​theo mô hình hệ số tương quan đều có các giá trị giữa -1 và 1.

Ví dụ 1.  Khảo sát áp suất trong bình thí nghiệm chất khí A theo thời gian được cho theo 2 biến dữ liệu thời gian và áp suất như sau


 Thời gian (phút)
 1
 1.5
 2
 3
 4
 6
 8
 12
 16
 24
 Áp suất
(atm)
 24
 16
 12
 8
 6
 4
 3
 2
 1.7
 1


Vẽ biểu đồ điểm rời rạc , tìm hệ số tương quan tuyến tính .


*Truy cập   http://www.alcula.com/calculators/statistics/scatter-plot/

Nhập dữ liệu sau , click SUBMIT DATA
1,1.5,2,3,4,6,8,12,16,24
24,16,12,8,6,4,3,2,1.7,1


Click Correlation coefficient , tìm hệ số tương quan


Để hiểu rõ chi tiết cách tính hệ số tương quan r , các bạn xem mô tả dưới đây

*Truy cập   http://www.socscistatistics.com/tests/pearson/Default2.aspx
Nhập dữ liệu vào 2 cột X-values , Y-values
Click Calculate R

Dựa vào hệ số r = -0.7089 ta có thể kết luận biến dữ liệu thời gian và áp suất không có tương quan tuyến tính mạnh .

13.2.2  Các công thức hệ số tương quan .
a.  Hệ số tương quan r-Pearson .

Hệ số tương quan Pearson khi áp dụng cho một mẫu có ký hiệu r và được xem là hệ số tương quan mẫu . Thay thế hiệp phương sai và phương sai tính trên mẫu ta có công thức sau cho 2 tập dữ liệu  {x1,...,xn} và  {y1,...,yn}  [1]
r = r_{xy} =\frac{\sum ^n _{i=1}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum ^n _{i=1}(x_i - \bar{x})^2} \sqrt{\sum ^n _{i=1}(y_i - \bar{y})^2}}
Trong đó :
  • n, x_i, y_i  được cho như trên
  • \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i (trung bình mẫu của {x1,...,xn})  ;  tương tự cho $\bar{y}$
Bằng cách sắp xếp lại ta thu được [2]
r = r_{xy} =\frac{n\sum x_iy_i-\sum x_i\sum y_i} {\sqrt{n\sum x_i^2-(\sum x_i)^2}~\sqrt{n\sum y_i^2-(\sum y_i)^2}}.
Trong đó :
  • n, x_i, y_i  được cho như trên
  • Thuật toán đơn chuyển này khá thuận lợi cho việc tính toán tương quan mẫu, nhưng tùy thuộc vào con số , đôi khi nó có thể không ổn định.
Chia tử và mẫu số cho n , rút gọn lại thì có  [3]
r = r_{xy} =\frac{\sum x_iy_i-n\bar{x}\bar{y}} {\sqrt{(\sum x_i^2-n\bar{x}^2)}~\sqrt{(\sum y_i^2-n\bar{y}^2)}}.
Trong đó :
  • n, x_i, y_i, \bar{x}, \bar{y}  được cho như trên
Một biểu thức tương đương của r được xem như là giá trị trung bình của tích các số tiêu chuẩn [4]
r = r_{xy} =\frac{1}{n-1} \sum ^n _{i=1} \left( \frac{x_i - \bar{x}}{s_x} \right) \left( \frac{y_i - \bar{y}}{s_y} \right)
Trong đó :
  • n, x_i, y_i, \bar{x}, \bar{y}  được cho như trên ,  s_x, s_y   được định nghĩa như sau
  • \left( \frac{x_i - \bar{x}}{s_x} \right)  là số tiêu chuẩn của x (tương tự cho y)
Ta cũng có thể sử dụng công thức thay thế sau đây cho r  [5]
r = r_{xy} =\frac{\sum x_iy_i-n \bar{x} \bar{y}}{(n-1) s_x s_y}
Trong đó :
  • n, x_i, y_i, \bar{x}, \bar{y}   được cho như trên , 
  • s_x=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2} (độ lệch tiêu chuẩn của x);  (tương tự cho  sy )

Ví dụ 2.   Cho các diểm dữ liệu sau  
(5,14),(9,17),(12,16),(14,18),(17,23) .
Tìm hệ số tương quan tuyến tính  r ?
Lời giải .

*Truy cập    http://www.alcula.com/calculators/statistics/correlation-coefficient/
Nhập dữ liệu như hình sau , click SUBMIT DATA


 b. Hệ số tương quan nội lớp ICC .
Trong thống kê, tương quan nội lớp - intraclass (hoặc hệ số tương quan intraclass, viết tắt là ICC) là một thống kê mô tả có thể được sử dụng khi các phép đo định lượng được thực hiện trên các đơn vị được tổ chức thành các nhóm. Nó mô tả cách kết hợp mạnh yếu các đơn vị trong cùng một nhóm giống nhau. Trong khi được xem như một loại tương quan, không giống như hầu hết các độ đo tương quan khác, ICC tính toán trên dữ liệu có cấu trúc như các nhóm, chứ không phải là dữ liệu có cấu trúc như quan sát ghép cặp .

Mối tương quan intraclass thường được sử dụng để định lượng mức độ mà đối với nó các cá nhân với một mức độ cố định về mối quan hệ (ví dụ anh chị em ruột) giống nhau về một số lượng tính trạng nào đó (di truyền). Một ứng dụng nổi bật là việc đánh giá tính nhất quán hoặc lặp lại của các phép đo định lượng được thực hiện bởi nhiều quan sát khác nhau đo trên cùng số lượng.

Xét một tập dữ liệu gồm N cặp giá trị dữ liệu  (xn,1, xn,2), với  n = 1, ..., N .  Tương quan nội lớp  r được đề xuất bởi Ronald Fisher là  [1]
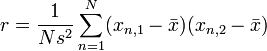r = \frac{1}{Ns^2} \sum_{n=1}^{N} (x_{n,1} - \bar{x}) ( x_{n,2} - \bar{x}) ,
Trong đó
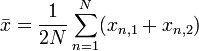\bar{x} = \frac{1}{2N} \sum_{n=1}^{N} (x_{n,1} + x_{n,2}) ,
s^2 = \frac{1}{2N} \left\{ \sum_{n=1}^{N} ( x_{n,1} - \bar{x})^2 + \sum_{n=1}^{N} ( x_{n,2} - \bar{x})^2 \right\} .
Các phiên bản sau của thống kê này sử dụng độ tự do (2N -1)  ở mẫu số để tính s2   và  (N -1)  ở mẫu số để tính r.  Sự khác biệt chính giữa ICC này và tương quan r-Pearson là các dữ liệu được gộp lại để ước tính giá trị trung bình và phương sai.  Giống như sự tương quan  r-Pearson , hệ số tương quan nội lớp cho dữ liệu ghép cặp được giới hạn trong khoảng [-1, 1].

Mối tương quan nội lớp - intraclass cũng được xác định cho các tập dữ liệu với các nhóm có nhiều hơn 2 giá trị. Đối với nhóm gồm 3 giá trị, nó được định nghĩa  [2]

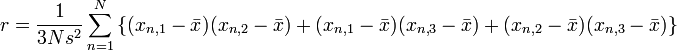r = \frac{1}{3Ns^2} \sum_{n=1}^{N} \left\{ ( x_{n,1} - \bar{x})( x_{n,2} - \bar{x}) + (x_{n,1} - \bar{x})( x_{n,3} - \bar{x})+( x_{n,2} - \bar{x})( x_{n,3} - \bar{x}) \right\} ,
Trong đó
\bar{x} = \frac{1}{3 N} \sum_{n=1}^{N} (x_{n,1} + x_{n,2} + x_{n,3}) ,
s^2 = \frac{1}{3N} \left\{ \sum_{n=1}^{N} ( x_{n,1} - \bar{x})^2 + \sum_{n=1}^{N} ( x_{n,2} - \bar{x})^2 + \sum_{n=1}^{N} ( x_{n,3} - \bar{x})^2\right\} .
Khi số lượng các giá trị cho mỗi nhóm tăng lên , dạng tương đương của ICC là  [3]

r = \frac{K}{K-1}\cdot\frac{N^{-1}\sum_{n=1}^N(\bar{x}_n-\bar{x})^2}{s^2} - \frac{1}{K-1},
Trong đó K là số các giá trị dữ liệu trong mỗi nhóm, và  $\bar{x}$  là trung bình mẫu của nhóm thứ n .
Nếu K lớn thì công thức ICC xấp xỉ với  [4]

\frac{N^{-1}\sum_{n=1}^N(\bar{x}_n-\bar{x})^2}{s^2},

Ví dụ 3.   Khảo sát mức điều chỉnh của 20 máy đo với các dữ liệu có trong bảng sau 
Tìm hệ số tương quan nội lớp  r ?



Máy đo thứ
Mức điều chỉnh  A
Mức điều chỉnh  B
Mức điều chỉnh  C
Mức điều chỉnh  D
1
-0.8
-0.6
-0.1
0.5
2
-2
-1.9
-1.9
-2.0
3
-1.1
-1.2
-0.7
-0.5
4
1.6
1.7
1.8
1.7
5
0.9
1.3
1.5
1.6
6
-0.4
-0.5
-0.2
-0.3
7
-1.5
-1.2  
-0.5 
-0.9
8
2.0   
2.1
2.1  
2.0
9
-0.8 
-0.6  
-0.5 
-0.1
10
-1.2 
-1.0
-1.1 
-0.5
11
0.0   
0.2   
0.2
0.3
12
-1.0 
-0.5  
-0.1
-0.1
13
1.5   
1.6   
1.9
0.5
14
-1.0 
-0.8
-0.1
-0.1
15
0.2   
0.5   
0.8   
1.0
16
-1.8
-1.5
-1.4
-1.4
17
-1.2
-0.9  
-0.7  
-0.5
18
-1.3 
-1.0  
-0.5 
-0.4
19
1.2  
1.2   
1.3  
1.4
20
-0.4 
-0.2
0.2  
0.4




 
Lời giải .
*Truy cập    https://www.statstodo.com/ICC_Pgm.php#
Nhập dữ liệu như hình sau

-0.8  -0.6  -0.1   0.5
-2    -1.9  -1.9  -2.0
-1.1  -1.2  -0.7  -0.5
1.6    1.7   1.8   1.7
0.9    1.3   1.5   1.6
-0.4  -0.5  -0.2  -0.3
-1.5  -1.2  -0.5  -0.9
2.0    2.1   2.1   2.0
-0.8  -0.6  -0.5  -0.1
-1.2  -1.0  -1.1  -0.5
0.0    0.2   0.2   0.3
-1.0  -0.5  -0.1  -0.1
1.5    1.6   1.9   0.5
-1.0  -0.8  -0.1  -0.1
0.2    0.5   0.8   1.0
-1.8  -1.5  -1.4  -1.4
-1.2  -0.9  -0.7  -0.5
-1.3  -1.0  -0.5  -0.4
1.2    1.2   1.3   1.4
-0.4  -0.2   0.2   0.4

Click Calculate Intraclass Correlation from Data


Một địa chỉ khác khá tốt để tìm hệ số tương quan nội lớp - intraclass

*Truy cập    http://department.obg.cuhk.edu.hk/researchsupport/IntraClass_correlation.asp


Ví dụ 4.   Khảo sát chiều dài của thai nhi trong tử cung, có thể dùng x-ray (col 1), siêu âm (col 2), hoặc cộng hưởng từ (col 3)  với máy đo với các dữ liệu có trong bảng sau cho 4 trẻ sơ sinh
1.1, 1.2, 1.5; 
2.2, 2.1, 2.0; 
6.3, 6.1, 6.8; 
9.4, 9.5, 9.0.
Tìm hệ số tương quan nội lớp  r ?







*Truy cập    https://www.statstodo.com/ICC_Pgm.php#
Nhập dữ liệu như hình sau

1.1  1.2  1.5

2.2  2.1  2.0

6.3  6.1  6.8

9.4  9.5  9.0


Hệ số ICC = 0,9956, phân tích phương sai F = 0,13. Không có sự khác biệt đáng kể giữa các thứ hạng, và mức độ của sự phù hợp là rất cao.



c. Hệ số tương quan bậc Spearman .
Trong thống kê, hệ số tương quan bậc Spearman ký hiệu $r_s$, là một độ đo phi tham số về sự phụ thuộc thống kê giữa hai biến. Nó đánh giá mức độ mạnh yếu về mối quan hệ giữa hai biến và có thể được mô tả bằng một hàm số đơn điệu. Nếu không có giá trị dữ liệu lặp lại, một tương quan Spearman hoàn hảo có hệ số  +1 hoặc -1 xảy ra khi mỗi biến là một hàm đơn điệu hoàn hảo theo biến kia.
Nếu n bậc là các số nguyên rời rạc công thức của hệ số tương quan bậc Spearman là  [1]

r_s = {1- \frac {6 \sum d_i^2}{n(n^2 - 1)}}.
Trong đó
  • d_i = rg(X_i) - rg(Y_i),  là sai biệt giữa 2 bậc của mỗi quan sát
  • n là số quan sát 
Ví dụ 5.   Khảo sát độ tương quan giữa chỉ số IQ và số giờ xem TV trong một tuần của 10 sinh viên các dữ liệu được cho như sau

IQ,$X_i$  số giờ xem TV / tuần,$Y_i$
106    7
86    0
100  27
101  50
99               28
103 29
97 20
113 12
112 6
110 17
Thực hiện các bước tính
  1. Sắp thứ tự các dữ liệu của cột thứ nhất ($X_i$). Tạo một cột mới là  $x_i$  và đánh số thứ tự  1,2,3,...n.
  2. Sắp thứ tự các dữ liệu của cột thứ hai ($Y_i$). Tạo một cột mới là $y_i$ và đánh số thứ tự  1,2,3,...n.
  3. Tạo một cột $d_i$ tính các sai biệt về thứ tự giữa ( $x_i$  và $y_i$  ).
  4. Tạo một cột  $d_i^2$  gồm các giá trị  $d_i$  bình phương .

Tính   \sum d_i^2 = 194. Tổng số quan sát  n = 10. Thay các trị số vào công thức : r_s = {1- \frac {6 \sum d_i^2}{n(n^2 - 1)}}.
ta thu được  $r_s = −0.17575 $
Giá trị này biểu thị mối tương quan giữa chỉ số IQ và số giờ xem truyền hình là rất thấp, mặc dù giá trị $r_s$ âm cho thấy rằng thời gian xem truyền hình càng nhiều thì chỉ số IQ lại càng thấp hơn.

*Truy cập    http://www.maccery.com/maths/spearmans-rank

Nhập dữ liệu như hình sau

7,0,27,50,28,29,20,12,6,17

106,86,100,101,99,103,97,113,112,110

 Click Calculate



13.2.3  Hệ số tương quan r-Pearson và hồi quy tuyến tính .
a.  Đường điều hóa tốt nhất BFL (Best-Fitted-Line) .

-Như đã biết ở phần 13a.  bạn luôn luôn có thể tìm được BFL cho bất kỳ tập điểm dữ liệu nào , nhưng làm thế nào biết được độ chính xác để đường thẳng tìm được có thể đáp ứng cho mô hình toán học đó ? 
-Nếu những điểm dữ liệu phân tán xa BFL thì đây là quan hệ tuyến tính yếu . Ngược lại nếu chúng tập trung gần với BFL ta có mối quan hệ tuyến tính mạnh , khi đó BFL có thể được dùng để tính toán cho những dự báo nội suy hoặc ngoại suy khá tốt .
-Độ mạnh của khuynh hướng tuyến tính có thể được mô tả bởi hệ số tương quan tuyến tính r-Pearson , ký‎ hiệu là  r và được tính theo công thức [2] .



Một cách tổng quát  ,  r  càng gần  -1  và  1 , khuynh hướng tuyến tính giữa x và y càng mạnh khi đó  BFL có thể áp dụng cho dự báo một cách đáng tin cậy  .  
Nếu  r gần  0  ,  quan hệ tuyến tinh giữa   x  và  y  yếu đi  , BFL không cho ta những kết quả dự báo tốt . 


Ví dụ 6.    Bảng dữ liệu sau chỉ ra tỷ lệ thất nghiệp và tổng thu nhập cá nhân tại Hoa Kỳ theo các năm tương ứng .
Tìm hệ số tương quan tuyến tính  r ?

Năm
Tỷ lệ thất nghiệp
              ( % )
      Tổng thu nhập cá nhân
          (Tỷ  USD )
1975
                 8.5
                     1.3
1980
                 7.1
                     2.3
1985
                 7.2
                     3.4
1990
                 5.6
                     4.8
1995
                 5.6
                     6.1
2000
                 4.0
                     8.3

*Truy cập    http://www.alcula.com/calculators/statistics/correlation-coefficient/
Nhập dữ liệu như hình sau , click SUBMIT DATA



 
Nhập dữ liệu
8.5,7.1,7.2,5.6,5.6,4.0
1.3,2.3,3.4,4.8,6.1,8.3
Thu được  Correlation coefficient (r): -0.97043851620105
Có thể nói rằng khuynh hướng tuyến tính giữa x và y khá mạnh và có giá trị âm -0.9704 ( có tính nghịch biến ) nghĩa là tỷ lệ thất nghiệp gia tăng thì tổng thu nhập sẽ giảm đi . Trong trường hợp này  BFL có thể áp dụng cho dự báo ở phạm vi vừa phải một cách đáng tin cậy   . 

b. Tìm phương trình đường điều hóa BFL .

 *Truy cập    http://www.mathportal.org/calculators/statistics-calculator/correlation-and-regression-calculator.php

Nhập dữ liệu vào Enter X Values , Enter Y Values
Để tạo bảng dữ liệu , click Use data grit to input x and y values
Tìm BFL , click  Find the equation of the regression line
Click  Compute

Ví dụ 7.    Bảng dữ liệu sau ở ví dụ 6 chỉ ra tỷ lệ thất nghiệp và tổng thu nhập cá nhân tại Hoa Kỳ theo các năm tương ứng .
Tìm phương trình đường điều hóa BFL ?



Xem trực tuyến
www.mathportal.org/calculators/statistics-calculator/correlation-and-regression-calculator.php?
hoặc    http://goo.gl/HN7vYI






Trần hồng Cơ
Ngày 10/02/2016




------------------------------------------------------------------------------------------- -

Những điều biết được chỉ là hạt cát , những điều chưa biết là cả một đại dương .

Isaac Newton


Người đăng: vào lúc Không có nhận xét nào :
Nhãn: , , , , , , , , , , ,
Đăng ký: Bài đăng ( Atom )

*******

Blog Toán Cơ trích đăng các thông tin khoa học tự nhiên của tác giả và nhiều nguồn tham khảo trên Internet .
Blog cũng là nơi chia sẻ các suy nghĩ , ý tưởng về nhiều lĩnh vực khoa học khác nhau .


Chia xẻ

Bài viết được xem nhiều trong tuần

CÁC BÀI VIẾT MỚI VỀ CHỦ ĐỀ TOÁN HỌC

Danh sách Blog

Gặp Cơ tại Researchgate.net

Co Tran